
Concept explainers
In 1960, William K. Estes proposed the following model for measuring a student’s performance in the classroom:
where k(t) is the student’s knowledge after t weeks (expressed as a percentage and measured by performance on examinations), ℓ is a constant called the coefficient of learning and representing the student’s ability to learn (expressed as a percentage and determined by IQ or some similar general intelligence predictor), and λ is a constant representing the fraction of available time the student spends performing helpful acts that should increase knowledge of the subject (studying, going to class; and so on). Use this model to solve Problems 79 and 80.
80. Learning theory. Refer to Problem 79. When will both students have the same level of knowledge? Round answer to one decimal place.
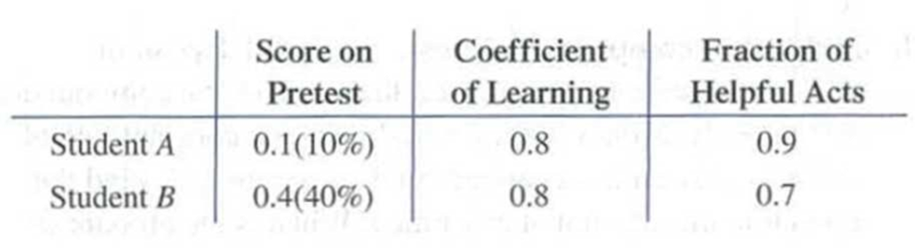
79. Learning theory. Students enrolled in a beginning Spanish class are given a pretest the first day of class to determine their knowledge of the subject. The results of the pretest, the coefficient of learning, and the fraction of time spent performing helpful acts for two students in the class are given in the table. Use the Estes model to predict the knowledge of each student after 6 weeks in the class.
Want to see the full answer?
Check out a sample textbook solution
Chapter 9 Solutions
EP CALCULUS F/BUS.,ECON.-BRIEF-ACCESS
- DETAILS MY NOTES SESSCALCET2 6.3.017. 1. [-/1 Points] Evaluate the integral. - - dy y(y + 2)(y-3) Need Help? Read It Watch It SUBMIT ANSWER 2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.027. Evaluate the integral. (Use C for the constant of integration.) X + 16 x²+10x29 dx Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardDo the Laplace Transformation for this equation in Partial Fractions.arrow_forwardUse undetermined coefficients to find the particular solution to y"-2y-4y=3t+6 Yp(t) =arrow_forward
- Car A starts from rest at t = 0 and travels along a straight road with a constant acceleration of 6 ft/s^2 until it reaches a speed of 60ft/s. Afterwards it maintains the speed. Also, when t = 0, car B located 6000 ft down the road is traveling towards A at a constant speed of 80 ft/s. Determine the distance traveled by Car A when they pass each other.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forward
- 4. Use method of separation of variable to solve the following wave equation მłu J²u subject to u(0,t) =0, for t> 0, u(л,t) = 0, for t> 0, = t> 0, at² ax²' u(x, 0) = 0, 0.01 x, ut(x, 0) = Π 0.01 (π-x), 0arrow_forwardSolve the following heat equation by method of separation variables: ди = at subject to u(0,t) =0, for -16024 ძx2 • t>0, 0 0, ux (4,t) = 0, for t> 0, u(x, 0) = (x-3, \-1, 0 < x ≤2 2≤ x ≤ 4.arrow_forwardex 5. important aspects. Graph f(x)=lnx. Be sure to make your graph big enough to easily read (use the space given.) Label all 6 33arrow_forwardDecide whether each limit exists. If a limit exists, estimate its value. 11. (a) lim f(x) x-3 f(x) ↑ 4 3- 2+ (b) lim f(x) x―0 -2 0 X 1234arrow_forwardDetermine whether the lines L₁ (t) = (-2,3, −1)t + (0,2,-3) and L2 p(s) = (2, −3, 1)s + (-10, 17, -8) intersect. If they do, find the point of intersection.arrow_forwardConvert the line given by the parametric equations y(t) Enter the symmetric equations in alphabetic order. (x(t) = -4+6t = 3-t (z(t) = 5-7t to symmetric equations.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





