
Concept explainers
Find the moment of inertia of the shaded area with respect to x axis
Answer to Problem 9.36P
The moment of inertia of the shaded area with respect to x axis
Explanation of Solution
Show the centroidal location of the given section as Figure 1.
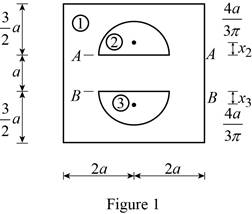
Consider x axis.
Consider the section 1.
Calculate the moment of inertia of the section 1
The expression for the area of the section 1 (A) as follows;
The expression for the centroid of the section 1 (d) as follows;
Calculate the moment of inertia of the section 1
Substitute
The expression for the moment of inertia of the section AA
The section AA and BB compressed of semi-circle.
The expression for the area of the semi-circle (A) as follows;
The expression for the centroid of the semi-circle (d) as follows;
Calculate the moment of inertia of the section 2
Since both sections (2) and (3) are semi-circle which has same moment of inertia.
Substitute
Consider the section 2.
The expression for the centroid of the section 2 (d) from neutral axis as follows;
Calculate the moment of inertia of the section 2
Substitute
Consider the section 3.
The expression for the centroid of the section 3 (d) from neutral axis as follows;
Calculate the moment of inertia of the section 3
Substitute
Calculate the total moment of inertia of the entire section
Substitute
Consider y axis.
Consider the section 1.
Calculate the moment of inertia of the section 1
The expression for the area of the section 1 (A) as follows;
The expression for the centroid of the section 1 (d) as follows;
Calculate the moment of inertia of the section 1
Substitute
Consider the section 2.
Calculate the moment of inertia of the section 2
Substitute
The expression for the area of the semi-circle (A) as follows;
The expression for the centroid of the semi-circle (d) as follows;
Calculate the moment of inertia of the section 1
Substitute
Since the section 2 and section 3 are same. Hence,
Calculate the total moment of inertia of the entire section
Substitute
Therefore, the moment of inertia of the shaded area with respect to x axis
Want to see more full solutions like this?
Chapter 9 Solutions
EBK VECTOR MECHANICS FOR ENGINEERS: STA
- Qu 2 Calcium oxide (CaO) a white, caustic, alkaline solid that reacts vigorously with water to produce calcium hydroxide, releasing heat in the process. It is used in various industrial applications, including cement production and water treatment. FA= 41{0 The ionic radii of the ions are: TCa2+= 0.100 nm and roz-= 0.140 nm. On the basis of this information answer the following questions: 1. What is the type of bonding that exists in CaO crystal? 2.Calculate attractive (Fs) force in [N] between a Ca'* iron and O* ifon that is separated by an equilibrium distance ro. Calculate repulsive (FR) force in [N] between a Ca?* iron and O? iron that is separated by an equilibrium distance ro. What is the magnitude of the net force FN?arrow_forwardShow work if any equations or calculations are used.What is the main alloying element and carbon percentage of SAE-AISI 4621 Steel?arrow_forwardThe particle has a mass of 0.5 kg and is confined to move along the smooth horizontal slot due to the rotation of the arm OA. Determine the force of the rod on the particle and the normal force of the Isot on the particle when 0 = 30°. The rod is rotating with a angular velocity of ė = 2rad/s and an angular acceleration of = 3rad/s². Assume the particle only contacts one side of the slot at any instant. To check your answer, please enter the normal force of the slot onto the particle in Newtons. A * = 2 rad/s -0- 0.5 marrow_forward
- Solve, use engineering economic tablesarrow_forwardSolve, use engineering economic tablesarrow_forwardQu 2 Calcium oxide (CaO) a white, caustic, alkaline solid that reacts vigorously with water to produce calcium hydroxide, releasing heat in the process. It is used in various industrial applications, including cement production and water treatment. The ionic radii of the ions are: TCa2+= 0.100 nm and roz-= 0.140 nm. On the basis of this information answer the following questions:Number 1 through 4 I need to show all work step by step problemsarrow_forward
- Show work if any equations or calculations are used. Assuming hole basis, find the shaft and hole dimensions for a sliding fit using a basic hole size of 20mm. Show the max and minimum size for both hole and shaft. Utilize the equations and tables in the appendix.arrow_forwardShow work if any equations or calculations are used. A milling machine is equipped with a 1” diameter end mill. During a facingoperation, the spindle is running at 275 RPM. The depth of cut is 0.04” and linear feed rate is 2” per minute. Find: (a) Cutting speed, (b) Material Removal Ratearrow_forwardL1 = 5.7m, L2 = 1m, L3 = 1.2m, L4 = 1m, L5 = 0.2, L6 = 0.5m, v2 = 4.8m/s. The solutions should include, but not be limited to, the equations used tosolve the problems, the charts used to solve the problems, detailed working,choice of variables, the control volume considered, justification anddiscussion of results etc.If determining the friction factor, the use of both Moody chart and empiricalequations should be used to verify the validity of the valuearrow_forward
- Please identify the marked points of the stress-strain curve (Write on graph next to corresponding letter) Stress, σ A D (slope of line) B. C Strain, &arrow_forwardr Q2. A bracket is attached to a vertical column by means of six identical bolts as shown in Fig. 1. It is subjected to an eccentric force of P-80 kN at a distance of 200 mm from the center of column. What is the magnitude of maximum shear force and which bolt carry it? P= 80 kN 200 Fig. 1 1 2- 75 6 30 75 → 5 .5 1- 50 10-50-1arrow_forward3. The attachment shown in the Fig.2 is made of 1040 HR. The static force is 30 kN. Specify the weldment (give the pattern, electrode number, type of weld, length of weld, and leg size). 30 kN Fig. 2 500 All dimension in mm 100 (15 marks)arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





