EP MATHEMATICS FOR THE TRADES
11th Edition
ISBN: 9780134758817
Author: SAUNDERS
Publisher: PEARSON CO
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 9.2, Problem 6BE
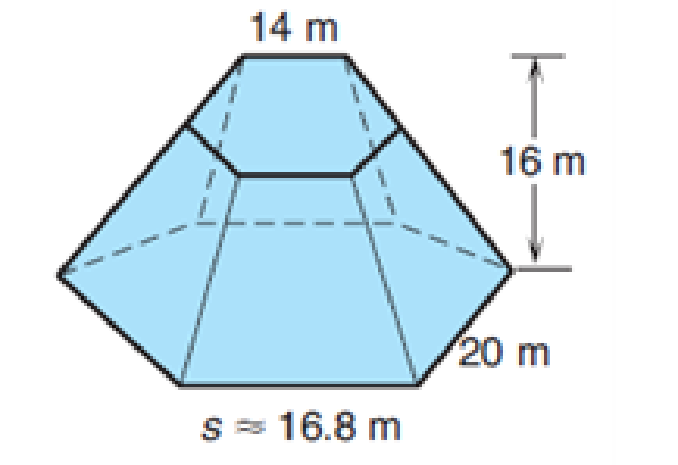
Find the total outside surface area and volume of the following solid objects. If necessary, round to the nearest whole number unless otherwise directed. (Assume that all bases are regular.)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Math 2 question. thx
Please help on this Math 1
Determine if the two statements are equalivalent using a truth table
Chapter 9 Solutions
EP MATHEMATICS FOR THE TRADES
Ch. 9.1 - What is the perimeter of a regular hexagon with...Ch. 9.1 - Find the area:Ch. 9.1 - Find the volume of each of the following right...Ch. 9.1 - Find the volume of each of the following right...Ch. 9.1 - Find the volume of each of the following right...Ch. 9.1 - Find the volume of each of the following right...Ch. 9.1 - Prob. 5AECh. 9.1 - Find the volume of each of the following right...Ch. 9.1 - Find the volume of each of the following right...Ch. 9.1 - Find the volume of each of the following right...
Ch. 9.1 - Find the lateral surface area and the volume of...Ch. 9.1 - Find the lateral surface area and the volume of...Ch. 9.1 - Find the lateral surface area and the volume of...Ch. 9.1 - Find the lateral surface area and the volume of...Ch. 9.1 - Find the lateral surface area and the volume of...Ch. 9.1 - Find the lateral surface area and the volume of...Ch. 9.1 - C. Find the total outside surface area and the...Ch. 9.1 - C. Find the total outside surface area and the...Ch. 9.1 - C. Find the total outside surface area and the...Ch. 9.1 - C. Find the total outside surface area and the...Ch. 9.1 - C. Find the total outside surface area and the...Ch. 9.1 - C. Find the total outside surface area and the...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.1 - Practical Applications. Round to the nearest tenth...Ch. 9.2 - What type of triangle has two equal sides?Ch. 9.2 - What is the formula for the area of an equilateral...Ch. 9.2 - Prob. 1AECh. 9.2 - Prob. 2AECh. 9.2 - Prob. 3AECh. 9.2 - Prob. 4AECh. 9.2 - Prob. 5AECh. 9.2 - Prob. 6AECh. 9.2 - Prob. 7AECh. 9.2 - Prob. 8AECh. 9.2 - Find the total outside surface area and volume of...Ch. 9.2 - Find the total outside surface area and volume of...Ch. 9.2 - Find the total outside surface area and volume of...Ch. 9.2 - Find the total outside surface area and volume of...Ch. 9.2 - Find the total outside surface area and volume of...Ch. 9.2 - Find the total outside surface area and volume of...Ch. 9.2 - Find the total outside surface area and volume of...Ch. 9.2 - B. Find the total outside surface area and volume...Ch. 9.2 - Prob. 1CECh. 9.2 - C. Practical Applications Metalworking A...Ch. 9.2 - Prob. 3CECh. 9.2 - C. Practical Applications Agriculture How many...Ch. 9.2 - C. Practical Applications Sheet Metal Trades How...Ch. 9.2 - C. Practical Applications Construction How many...Ch. 9.3 - What is the formula for the circumference of a...Ch. 9.3 - Find the area of a circle with diameter 10 cm....Ch. 9.3 - Find the lateral surface area and volume of each...Ch. 9.3 - Find the lateral surface area and volume of each...Ch. 9.3 - Find the lateral surface area and volume of each...Ch. 9.3 - Find the lateral surface area and volume of each...Ch. 9.3 - Find the lateral surface area and volume of each...Ch. 9.3 - Find the lateral surface area and volume of each...Ch. 9.3 - Find the total surface area and volume of each of...Ch. 9.3 - Find the total surface area and volume of each of...Ch. 9.3 - Find the total surface area and volume of each of...Ch. 9.3 - Find the total surface area and volume of each of...Ch. 9.3 - Find the total surface area and volume of each of...Ch. 9.3 - Find the total surface area and volume of each of...Ch. 9.3 - Practical Applications. (Round to the nearest...Ch. 9.3 - Practical Applications. (Round to the nearest...Ch. 9.3 - Practical Applications. (Round to the nearest...Ch. 9.3 - Practical Applications. (Round to the nearest...Ch. 9.3 - Practical Applications. (Round to the nearest...Ch. 9.3 - Practical Applications. (Round to the nearest...Ch. 9.3 - Practical Applications. (Round to the nearest...Ch. 9.3 - Industrial Technology How high should a 50-gal...Ch. 9.3 - Plumbing A marble-top bathroom sink has the shape...Ch. 9.3 - Sheet Metal Trades How many square inches of sheet...Ch. 9.3 - Machine Trades What is the weight of the bushing...Ch. 9.3 - Manufacturing Find the capacity in gallons of the...Ch. 9.3 - Plumbing A septic tank has the shape shown in the...Ch. 9.3 - Construction How many cubic yards of concrete are...Ch. 9.3 - Machine Trades At a density of 0.0925 lb/in.3,...Ch. 9.3 - Painting A spherical tank has a diameter of 16.5...Ch. 9.3 - Industrial Technology A cylindrical tank 72 cm in...Ch. 9.3 - Agriculture The water tower shown in the figure...Ch. 9.3 - Automotive Trades In an automobile engine, the...Ch. 9.3 - Automotive Trades A cylindrical hose 24 in. long...Ch. 9.3 - Agriculture The water trough shown in the figure...Ch. 9.3 - Painting The metal silo shown in the figure has a...Ch. 9.3 - Construction An outdoor cylindrical fire pit has...Ch. 9.3 - Water/Wastewater Treatment Due to a rupture in a...Ch. 9.3 - Manufacturing If a particular extrusion process is...Ch. 9.4 - Find c:Ch. 9.4 - Prob. 2LCCh. 9.4 - Find the lateral surface area and volume of each...Ch. 9.4 - Find the lateral surface area and volume of each...Ch. 9.4 - Find the lateral surface area and volume of each...Ch. 9.4 - Find the lateral surface area and volume of each...Ch. 9.4 - Prob. 1BECh. 9.4 - Prob. 2BECh. 9.4 - Find the lateral surface area and volume of each...Ch. 9.4 - Find the lateral surface area and volume of each...Ch. 9.4 - Prob. 1CECh. 9.4 - Find the volume of each figure. (Use 3.14 and...Ch. 9.4 - Find the volume of each figure. (Use 3.14 and...Ch. 9.4 - Find the volume of each figure. (Use 3.14 and...Ch. 9.4 - Prob. 1DECh. 9.4 - Prob. 2DECh. 9.4 - Prob. 3DECh. 9.4 - Practical Applications. (Round to the nearest...Ch. 9.4 - Prob. 5DECh. 9.4 - Practical Applications. (Round to the nearest...Ch. 9.4 - Practical Applications. (Round to the nearest...Ch. 9.4 - Practical Applications. (Round to the nearest...Ch. 9.4 - Prob. 9DECh. 9.4 - Welding A cone-shaped hopper is constructed by...Ch. 9.4 - Prob. 11DECh. 9.4 - Practical Applications. (Round to the nearest...Ch. 9.4 - Practical Applications. (Round to the nearest...Ch. 9 - Identify solid figures, including prisms, cubes,...Ch. 9 - Find the surface area and volume of solid objects....Ch. 9 - Solve practical problems involving solid figures....Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Prob. 12APSCh. 9 - Prob. 13APSCh. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Prob. 17APSCh. 9 - Solve the following problems involving solid...Ch. 9 - Solve the following problems involving solid...Ch. 9 - Prob. 20APSCh. 9 - Prob. 21APSCh. 9 - Practical Applications Manufacturing How many...Ch. 9 - Practical Applications Construction How many cubic...Ch. 9 - Practical Applications Metalworking What is the...Ch. 9 - Practical Applications Plumbing What is the...Ch. 9 - Practical Applications Painting How many quarts of...Ch. 9 - Practical Applications Construction A hole must be...Ch. 9 - Practical Applications Manufacturing How many...Ch. 9 - Practical Applications Industrial Technology What...Ch. 9 - Practical Applications Automotive Trades At a...Ch. 9 - Practical Applications Masonry A slim jumbo...Ch. 9 - Practical Applications Construction A foundation...Ch. 9 - Practical Applications Manufacturing How many...Ch. 9 - Practical Applications Construction How many cubic...Ch. 9 - Practical Applications Sheet Metal Trades How many...Ch. 9 - Practical Applications Industrial Technology Find...Ch. 9 - Prob. 16BPSCh. 9 - Prob. 17BPSCh. 9 - Practical Applications Welding A rectangular tank...Ch. 9 - Practical Applications Automotive Trades An oil...Ch. 9 - Practical Applications Welding Calculate the...Ch. 9 - Prob. 21BPSCh. 9 - Practical Applications Welding Calculate the...Ch. 9 - Masonry A square pillar is built using 1558...Ch. 9 - Landscaping In the figure shown below, the solid...Ch. 9 - Carpentry A granite kitchen countertop is 1516 in....Ch. 9 - Prob. 26BPSCh. 9 - Prob. 27BPSCh. 9 - Prob. 28BPSCh. 9 - Prob. 29BPSCh. 9 - Prob. 30BPSCh. 9 - Landscaping A landscape contractor needs to fill...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Question 3: p and q represent the following simple statements. p: Calgary is the capital of Alberta. A) Determine the value of each simple statement p and q. B) Then, without truth table, determine the va q: Alberta is a province of Canada. for each following compound statement below. pvq р^~q ~рл~q ~q→ p ~P~q Pq b~ (d~ ← b~) d~ (b~ v d) 0 4arrow_forward2. Let X be a random variable. (a) Show that, if E X2 = 1 and E X4arrow_forward18. If m n compute the gcd (a² + 1, a² + 1) in terms of a. [Hint: Let A„ = a² + 1 and show that A„|(Am - 2) if m > n.]arrow_forward2. (5 points) Let f(x) = = - - - x² − 3x+7. Find the local minimum and maximum point(s) of f(x), and write them in the form (a, b), specifying whether each point is a minimum or maximum. Coordinates should be kept in fractions. Additionally, provide in your answer if f(x) has an absolute minimum or maximum over its entire domain with their corresponding values. Otherwise, state that there is no absolute maximum or minimum. As a reminder, ∞ and -∞ are not considered absolute maxima and minima respectively.arrow_forwardLet h(x, y, z) = — In (x) — z y7-4z - y4 + 3x²z — e²xy ln(z) + 10y²z. (a) Holding all other variables constant, take the partial derivative of h(x, y, z) with respect to x, 2 h(x, y, z). მ (b) Holding all other variables constant, take the partial derivative of h(x, y, z) with respect to y, 2 h(x, y, z).arrow_forwardmath help plzarrow_forward1. Show that, for any non-negative random variable X, EX+E+≥2, X E max X. 21.arrow_forwardFor each real-valued nonprincipal character x mod k, let A(n) = x(d) and F(x) = Σ : dn * Prove that F(x) = L(1,x) log x + O(1). narrow_forwardBy considering appropriate series expansions, e². e²²/2. e²³/3. .... = = 1 + x + x² + · ... when |x| < 1. By expanding each individual exponential term on the left-hand side the coefficient of x- 19 has the form and multiplying out, 1/19!1/19+r/s, where 19 does not divide s. Deduce that 18! 1 (mod 19).arrow_forwardProof: LN⎯⎯⎯⎯⎯LN¯ divides quadrilateral KLMN into two triangles. The sum of the angle measures in each triangle is ˚, so the sum of the angle measures for both triangles is ˚. So, m∠K+m∠L+m∠M+m∠N=m∠K+m∠L+m∠M+m∠N=˚. Because ∠K≅∠M∠K≅∠M and ∠N≅∠L, m∠K=m∠M∠N≅∠L, m∠K=m∠M and m∠N=m∠Lm∠N=m∠L by the definition of congruence. By the Substitution Property of Equality, m∠K+m∠L+m∠K+m∠L=m∠K+m∠L+m∠K+m∠L=°,°, so (m∠K)+ m∠K+ (m∠L)= m∠L= ˚. Dividing each side by gives m∠K+m∠L=m∠K+m∠L= °.°. The consecutive angles are supplementary, so KN⎯⎯⎯⎯⎯⎯∥LM⎯⎯⎯⎯⎯⎯KN¯∥LM¯ by the Converse of the Consecutive Interior Angles Theorem. Likewise, (m∠K)+m∠K+ (m∠N)=m∠N= ˚, or m∠K+m∠N=m∠K+m∠N= ˚. So these consecutive angles are supplementary and KL⎯⎯⎯⎯⎯∥NM⎯⎯⎯⎯⎯⎯KL¯∥NM¯ by the Converse of the Consecutive Interior Angles Theorem. Opposite sides are parallel, so quadrilateral KLMN is a parallelogram.arrow_forwardBy considering appropriate series expansions, ex · ex²/2 . ¸²³/³ . . .. = = 1 + x + x² +…… when |x| < 1. By expanding each individual exponential term on the left-hand side and multiplying out, show that the coefficient of x 19 has the form 1/19!+1/19+r/s, where 19 does not divide s.arrow_forwardLet 1 1 r 1+ + + 2 3 + = 823 823s Without calculating the left-hand side, prove that r = s (mod 823³).arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGALGlencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillElementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage LearningMathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
What is a Prism? | Types of Prism | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=wxDTrgnyu28;License: Standard YouTube License, CC-BY