ENGINEERING MECHANICS
14th Edition
ISBN: 9780136522409
Author: HIBBELER
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 9.2, Problem 10FP
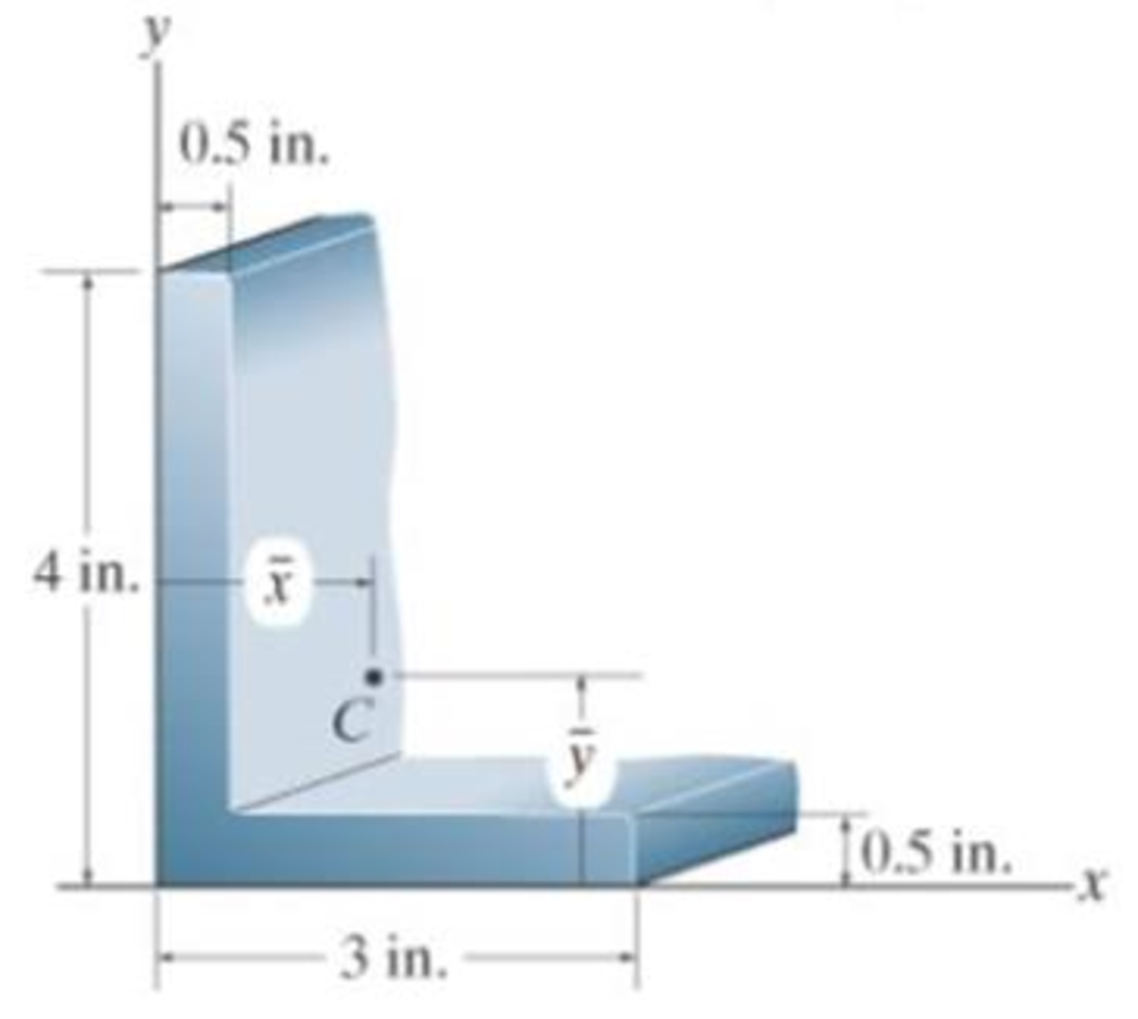
Locate the centroid
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Calculate the maximum shear stress Tmax at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m.
The following choices are provided in units of MPa and rounded to three decimal places.
Select one:
○ 1.2681.818
O 2. 25745.455
O 3. 17163.636
O 4. 10727.273
○ 5.5363.636
If L-719.01 mm, = 7839.63 N/m³, the normal stress σ caused by self-weight at the location of the maximum normal stress in the bar can be calculated as
(Please select the correct value of σ given in Pa and rounded to three decimal places.)
Select one:
○ 1. 1409.193
2. 845.516
O 3. 11273.545
○ 4.8455.159
○ 5.4509.418
6. 2818.386
7.5636.772
To calculate the rotation at Point B, a suitable virtual structure needs to be created.
Which equation in the following choices most accurately represents the functional relationship between the bending moment, Mv2 ( Units: N.mm), of the virtual
structure and the spatial coordinate x (Units: mm) if the applied unit virtual moment is clockwise?
Select one:
O 1. Mv2 1.000
O 2. Mv2=x+1.000
O 3. Mv2=x+0.000
4. Mv2 = -x-1.000
O 5. Mv2 -1.000
6. Mv2=-x+0.000
Chapter 9 Solutions
ENGINEERING MECHANICS
Ch. 9.1 - In each case, use the element shown and specify...Ch. 9.1 - Determine the centroid (x,y) of the shaded area....Ch. 9.1 - Determine the centroid (x,y) of the shaded area....Ch. 9.1 - Determine the centroid of the shaded area. Prob....Ch. 9.1 - Locate the center of mass x of the straight rod if...Ch. 9.1 - Locate the centroid of the homogeneous solid...Ch. 9.1 - Locate the centroid z of the homogeneous solid...Ch. 9.1 - Locate the center of mass of the homogeneous rod...Ch. 9.1 - Determine the location (x,y) of the centroid of...Ch. 9.1 - If the rod has a weight per unit length of 100...
Ch. 9.1 - Locate the center of gravity of the homogeneous...Ch. 9.1 - Determine the distance to the center of gravity...Ch. 9.1 - Locate the centroid of the area.Ch. 9.1 - Locate the centroid x of the parabolic area. Prob....Ch. 9.1 - Locate the centroid of the shaded area. Prob. 9-8Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the area. Probs. 9-11/12Ch. 9.1 - Locate the centroid of the area. Probs. 9-11/12Ch. 9.1 - Locate the centroid x of the area. Probs. 9-13/14Ch. 9.1 - Locate the centroid of the area. Probs. 9-13/14Ch. 9.1 - Solve the problem by evaluating the integrals...Ch. 9.1 - Solve the problem by evaluating the integrals...Ch. 9.1 - Locate the centroid of the area. Prob. 9-17Ch. 9.1 - Locate the centroid x of the area. Probs. 9-18/19Ch. 9.1 - Locate the centroid of the area. Probs. 9-18/19Ch. 9.1 - Locate the centroid of the shaded area.Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Determine the location of its center of gravity....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the area. Probs. 9-32/33Ch. 9.1 - Locate the centroid of the area. Probs. 9-32/33Ch. 9.1 - Determine the location of its center of mass. Also...Ch. 9.1 - Locate the centroid x of the shaded area. Probs....Ch. 9.1 - Locate the centroid of the shaded area. Probs....Ch. 9.1 - Locate the centroid x of the circular sector.Ch. 9.1 - Determine the location r of the centroid C for the...Ch. 9.1 - The material is homogeneous. Prob. 9-39Ch. 9.1 - Locate the centroid of the paraboloid. Probs....Ch. 9.1 - Locate the centroid z of the frustum of the...Ch. 9.1 - Determine the centroid of the solid. Prob. 9-42Ch. 9.1 - Locate the centroid of the quarter-cone. Prob....Ch. 9.1 - Determine its mass and the distance z to the...Ch. 9.1 - Locate the centroid z of the volume. Prob. 9-45Ch. 9.1 - Locate the centroid of the ellipsoid of...Ch. 9.1 - Locate the center of gravity z of the solid. Prob....Ch. 9.1 - Locate the centroid of the ellipsoid of...Ch. 9.1 - Locate the centroid z of the spherical segment....Ch. 9.1 - Suggestion: Use a triangular plate element...Ch. 9.2 - Locate the centroid (x,y,z) of the wire bent in...Ch. 9.2 - Locate the centroid of the beams cross-sectional...Ch. 9.2 - Locate the centroid of the beams cross-sectional...Ch. 9.2 - Locate the centroid (x,y) of the cross-sectional...Ch. 9.2 - Locate the center of mass (x,y,z) of the...Ch. 9.2 - Determine the center of mass (x,y,z) of the...Ch. 9.2 - If the mass of the gusset plates at the joints and...Ch. 9.2 - Determine the location (x,y,z) of the centroid of...Ch. 9.2 - Determine the location (x,y) of the centroid of...Ch. 9.2 - Neglect the thickness of the material and slight...Ch. 9.2 - Neglect the thickness of the material and slight...Ch. 9.2 - Each plate has a constant width in the z direction...Ch. 9.2 - Neglect the thickness of each segment. The mass...Ch. 9.2 - Neglect the size of the corner welds at A and B...Ch. 9.2 - Prob. 59PCh. 9.2 - Locate the centroid for the beams cross-sectional...Ch. 9.2 - Determine the location of the centroid C of the...Ch. 9.2 - Locate the centroid (x,y) of the shaded area....Ch. 9.2 - Neglect the size of the corner welds at A and B...Ch. 9.2 - Locate the centroid (x,y) of the shaded area....Ch. 9.2 - Determine the location (x,y) of the centroid C of...Ch. 9.2 - The beam is symmetric with respect to the y axis....Ch. 9.2 - Assume all corners are square and neglect the size...Ch. 9.2 - Prob. 68PCh. 9.2 - If it is folded over as shown, determine the...Ch. 9.2 - Locate the center of mass z of the forked level...Ch. 9.2 - Prob. 71PCh. 9.2 - Prob. 72PCh. 9.2 - Prob. 73PCh. 9.2 - The location of the center of gravity of each...Ch. 9.2 - Locate the center of mass (x,y,z) of the...Ch. 9.2 - Determine the location (x,y,z) of its centroid....Ch. 9.2 - It the cord is cut, the part will rotate about the...Ch. 9.2 - Prob. 78PCh. 9.2 - Prob. 79PCh. 9.2 - Prob. 80PCh. 9.2 - The assembly is made from a steel hemisphere. st =...Ch. 9.2 - The assembly is made from a steel hemisphere, st =...Ch. 9.2 - Prob. 83PCh. 9.2 - Determine the distance h to which a...Ch. 9.2 - Determine the distance z to the centroid of the...Ch. 9.2 - The cylinder and the cone are made from materials...Ch. 9.2 - Major floor loadings in a shop are caused by the...Ch. 9.2 - Determine the distance x to its center of gravity...Ch. 9.2 - Determine the mass and location (x,y,z) of its...Ch. 9.3 - Determine the surface area and volume of the solid...Ch. 9.3 - Prob. 14FPCh. 9.3 - Determine the surface area and volume of the solid...Ch. 9.3 - Determine the surface area and volume of the solid...Ch. 9.3 - Prob. 90PCh. 9.3 - Prob. 91PCh. 9.3 - Determine the volume of the storage tank. Probs....Ch. 9.3 - Prob. 93PCh. 9.3 - Determine the total weight of the wall if the...Ch. 9.3 - Determine its volume.Ch. 9.3 - Prob. 96PCh. 9.3 - Determine the volume of concrete needed to...Ch. 9.3 - Do not include the area of the ends in the...Ch. 9.3 - Prob. 99PCh. 9.3 - Prob. 100PCh. 9.3 - Prob. 101PCh. 9.3 - Each gallon of paint can cover 250 ft2. Probs....Ch. 9.3 - Determine the surface area and the volume of the...Ch. 9.3 - Prob. 104PCh. 9.3 - Determine how many joules (J) are radiated within...Ch. 9.3 - Prob. 106PCh. 9.3 - Prob. 107PCh. 9.3 - Prob. 108PCh. 9.3 - Prob. 109PCh. 9.3 - Prob. 110PCh. 9.3 - Prob. 111PCh. 9.3 - Prob. 112PCh. 9.3 - Prob. 113PCh. 9.3 - Prob. 114PCh. 9.5 - Water has a density of = 1 Mg/m3. Prob. F9-17Ch. 9.5 - The specific weight of water is = 62.4 lb/ft3.Ch. 9.5 - Water has a density of = 1 Mg/m3. Prob. F9-19Ch. 9.5 - Water has a density of = 1 Mg/m3. Prob. F9-20Ch. 9.5 - The specific weight of water is = 62.4 lb/ft3....Ch. 9.5 - Determine the magnitude of the resultant force and...Ch. 9.5 - Determine the magnitude of the resultant force and...Ch. 9.5 - The load over the plate varies linearly along the...Ch. 9.5 - The load is defined by the expression p = p0 sin...Ch. 9.5 - If this pressure loading acts uniformly along the...Ch. 9.5 - For the condition of high tide shown, determine...Ch. 9.5 - Determine the resultant force the water exerts on...Ch. 9.5 - If the density of concrete is c = 2.5 Mg/m3, and...Ch. 9.5 - Determine this factor if the concrete has a...Ch. 9.5 - Determine the magnitude of the resultant...Ch. 9.5 - If it is filled to the top, determine the...Ch. 9.5 - Prob. 126PCh. 9.5 - Determine the reactions at these supports due to...Ch. 9.5 - The tank is filled with a liquid that has a...Ch. 9.5 - The gate has a width of 1.5 m. w = 1.0 Mg/m3....Ch. 9.5 - Prob. 130PCh. 9.5 - Locate the centroid x of the area.Ch. 9.5 - Locate the centroid of the area.Ch. 9.5 - Prob. 3RPCh. 9.5 - Locate the centroid of the rod. Prob. R9-4Ch. 9.5 - Prob. 5RPCh. 9.5 - Prob. 6RPCh. 9.5 - Determine the volume of material required to make...Ch. 9.5 - Prob. 8RPCh. 9.5 - Determine the horizontal and vertical components...Ch. 9.5 - Determine the magnitude of the resultant...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The vertical deflection at Point B can be calculated as ( The following choices are provided in units of mm and rounded to three decimal places ; the downward deflection is negative and upward deflection is positive. ) Select one: 1. 1703.065 2. -1703.065 3. -2043.679 4.1362.452 5. -1362.452 6. 2043.679arrow_forwardThe second moments of area about z-axis, /z, and the second moments of area about y-axis, ly, can be calculated as Select one: O 1. I = Iz ○ 2. Ly ○ 3. ○ 4. ○ 5. = = Iz = *D' 64 I₁ = D, Iz Ly Ly = 32 *D' = = 3 Iz = *D' 32 = *D' O 6. Iy=D, Ly = D², Iz = 32 O 7. Ly = Iz D = 64 32arrow_forward[If L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam.] Step -2 Which equation in the following choices most accurately represents the functional relationship between the value of the slope O (Units: Radian) at half length (x = L/2) of the beam and the second moment of area about z-axis, Izz (Units: mm²), of the cross section? (Please note that " X = L/2" is the same as "X = L ÷ 2" .) Select one: O 1.0 448787.925/Izz O 2.0 279167.292/Izz O 3.0 38871.395/Izz O 4.0 114847.304/Izz O 5.0 176688.160/Izz O 6.0 609574.150/Izz O 7.0 70675.264/Izzarrow_forward
- Use the principle of virtual work to determine the vertical deflection and rotation at tip (Point B) of the cantilever shown below. (L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²) q Y M X A ΕΙ B L Step -1 Let the coordinates defined with origin located at B and x-axis pointing to the Left and Y-axis pointing upward. The bending moment, M (Units: N.mm), in the beam as a function of spatial coordinate x(Units: mm) can be most accurately described by Select one: 1. M=1126839.200 +2132.400*x*x 2. M=-1408549.000 - 3198.600*x*x 3. M=-1408549.000-2665.500*x*x 4. M=-1408549.000-2132.400*x*x 5. M= -1408549.000+2665.500*x*x 6. M= 1408549.000 + 2665.500*x*x 7. M= 1408549.000-2665.500*x*xarrow_forwardCalculate the principal stress σ at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places Select one: O 1.5363.64 O 2. 12872.727 3.9118.182 4. 10727.273 5. 16090.909 6. 2681.818arrow_forwardQuestion2 The mission profile for a jet driven aircraft consists of the following segments: engine start and warm-up, taxi, take-off, climb to the cruise altitude of 35000 ft, descend to 10000 ft, one hour loiter at this altitude at 60% of the cruise speed, flight at loiter speed and altitude to an alternate airport (100 nm), descend to landing approach condition followed by the final landing, taxi and shutdown. The cruise Mach number is 0.8. No provisions are made for the reserved fuel or any trapped oil and fuel. The aircraft carries 200 people (including pilots and the cabin crew) at 175 lb each and 90 lb baggage each. This aircraft has a wing area of 2000 ft² L/D at cruise L/D at 10000ft flight Table Q2 20 16 0.43 lb/hr/lb 0.50 lb/hr/lb C: Specific Fuel Consumption at cruise: C: Specific Fuel Consumption at 10000 ft flight: Weight ratios Engine Start and warm-up Taxi Take-off Climb Descent Landing, taxi and shutdown 0.992 0.996 0.996 0.996 0.992 0.992 Question 2 continues on the…arrow_forward
- Calculate the principal stress σ1_at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places. Select one: O 1.25745.455 O 2. 32181.818 3. 21454.545 4. 17163.636 5. 12872.727arrow_forwardCalculate the Von-Mises effective stress at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places Select one: O 1.27870.272 O2. 18580.181 3. 11148.109 O 4. 14864.145 O 5.22296.218arrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45°arrow_forward
- A close end tube of thin-walled circular section may be subjected to torque Tand internal pressure P, as shown in Figure Q3. The shear stress in the wall caused by the torque can be calculated as σ = T/(2πR²t), where the mean radius of the cross section is R(i.e., the radius of the centreline of the wall) and the wall thickness is t. The internal radius of the tube can be calculated as (R-t/2). However, as R>> t, you can approximately assume that the internal radius of the tube is equal to Rin the subsequent calculation. The tube is made from a material with Young's modulus E, Poisson's ratio v. Orr T Ozz бее буг Z бее T бел Figure Q3 Centreline of the wall Rarrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45° Aarrow_forward(If L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam.) Step-4 Which equation in the following choices most accurately represents the functional relationship between the value of the deflection, Vmax ( Units: mm) at the free end (XL) of the beam and the second moment of area about z-axis, Izz (Units: mm²) of the cross section ? (Please note that " X = L/2" is the same as "X = L ÷ 2" .) Select one: O 1. Vmax 1776823249.026 / Izz O 2. Vmax 516518386.345/Izz O 3. Vmax=743786476.336/Izz O 4. Vmax 1002045669.509/Izz O 5. Vmax 330571767.261/Izz O 6. Vmax 196276986.811 / Izz O 7. Vmax 1435921114.038/Izzarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Mechanical Engineering: Centroids & Center of Gravity (1 of 35) What is Center of Gravity?; Author: Michel van Biezen;https://www.youtube.com/watch?v=Tkyk-G1rDQg;License: Standard Youtube License