Chapter 9, Problem 93P

To determine

The velocity field.

The plot of velocity profile.

Answer to Problem 93P

The velocity field is $\frac{\rho g\sin \alpha }{2\mu }n\left(2h-n\right)$.

The plot of velocity profile is shown in figure below.

  

Explanation of Solution

Given information:

The flow is steady, incompressible, parallel, two dimensional and laminar. The velocity components are $u_s$ and $u_n$ and angle of wall is $\alpha$.

Write the expression for the continuity equation.

  $\frac{\partial u_s}{\partial s}+\frac{\partial u_n}{\partial n}=0$   ...... (I)

Here, The velocity components are $u_s$, and $u_n$ time is $t$ and position coordinates of flow field are $s$ and $n$.

Write the expression for the momentum conservation in n-direction.

  $\left(u_s\frac{\partial u_n}{\partial s}+u_n\frac{\partial u_n}{\partial n}\right)=-\frac{1}{\rho }\frac{\partial P}{\partial n}+\upsilon \left(\frac{{\partial }^2{u}_n}{\partial s^2}+\frac{{\partial }^2{u}_n}{\partial n^2}\right)+g_n$   ...... (II)

Here, pressure of the fluid is $P$, kinematic viscosity of fluid is $\upsilon$, gravity in n-direction is $g_n$.

Write the expression for the momentum conservation in s-direction.

  $\left(u_s\frac{\partial u_s}{\partial s}+u_n\frac{\partial u_s}{\partial n}\right)=-\frac{1}{\rho }\frac{\partial P}{\partial s}+\upsilon \left(\frac{{\partial }^2{u}_s}{\partial s^2}+\frac{{\partial }^2{u}_s}{\partial n^2}\right)+g_s$   ...... (III)

Here, gravity in s-direction is $g_s$.

Write the expression for the kinematic viscosity.

  $\upsilon =\frac{\mu }{\rho }$

Here, density is $\rho$ and dynamic viscosity is $\mu$.

Calculation:

Substitute $0$ for $u_n$ in Equation (I).

  $\begin{array}{l}\frac{\partial u_s}{\partial s}+\frac{\partial \left(0\right)}{\partial n}=0\\ \frac{\partial u_s}{\partial s}=0\end{array}$

Substitute $0$ for $u_n$, $0$ for $\frac{\partial u_s}{\partial s}$ and $-g\cos \alpha$ for $g_n$ in Equation (II).

  $\begin{array}{l}\left(u_s\left(0\right)+\left(0\right)\left(0\right)\right)=-\frac{1}{\rho }\frac{\partial P}{\partial n}+\upsilon \left(0+0\right)+\left(-g\cos \alpha \right)\\ 0=-\frac{1}{\rho }\frac{\partial P}{\partial n}-g\cos \alpha \\ \frac{\partial P}{\partial n}=-\rho g\cos \alpha \end{array}$   ...... (IV)

Integrate Equation (III) with respect to $n$.

  $P=-\rho gn\cos \alpha +f\left(s\right)$   ....... (V)

Substitute $h$ for $n$ and $P_{\text{atm}}$ for $P$ in Equation (IV).

  $\begin{array}{l}{P}_{\text{atm}}=-\rho gh\cos \alpha +f\left(s\right)\\ f\left(s\right)=P_{\text{atm}}+\rho gh\cos \alpha \end{array}$   ....... (VI)

Substitute $P_{\text{atm}}+\rho gh\cos \alpha$ for $f\left(s\right)$ in Equation (V).

  $\begin{array}{c}P=-\rho gn\cos \alpha +P_{\text{atm}}+\rho gh\cos \alpha \\ =P_{\text{atm}}+\rho g\left(h-n\right)\cos \alpha \end{array}$   ....... (VII)

Differentiate Equation (VII) with respect to $s$.

  $\frac{\partial P}{\partial s}=0$

Substitute $0$ for $u_n$, $0$ for $\frac{\partial u_s}{\partial s}$, $0$ for $\frac{\partial P}{\partial s}$ and $g\sin \alpha$ for $g_s$ in Equation (III).

  $\begin{array}{l}\left(u_s\left(0\right)+\left(0\right)\frac{\partial u_s}{\partial n}\right)=-\frac{1}{\rho }\left(0\right)+\upsilon \left(\left(0\right)+\frac{{\partial }^2{u}_s}{\partial n^2}\right)+\left(g\sin \alpha \right)\\ 0=\upsilon \frac{{\partial }^2{u}_s}{\partial n^2}+g\sin \alpha \\ \frac{{\partial }^2{u}_s}{\partial n^2}=\frac{-g\sin \alpha }{\upsilon }\end{array}$   ...... (VIII)

Integrate Equation (VIII) with respect to $n$.

  $\frac{\partial u_s}{\partial n}=\frac{-g\sin \alpha }{\upsilon }n+C_1$   ....... (IX)

Here, arbitrary constant is $C_1$.

Again, Integrate Equation (IX) with respect to $n$.

  $u_s=\frac{-g\sin \alpha }{2\upsilon }{n}^2+C_{1}n+C_2$   ...... (X)

Here, arbitrary constant is $C_2$.

Substitute $0$ for $u_s$ and $0$ for $n$ in Equation (X).

  $\begin{array}{l}0=\frac{-g\sin \alpha }{2\upsilon }{\left(0\right)}^2+C_1\left(0\right)+C_2\\ 0=0+0+C_2\\ C_2=0\end{array}$

Substitute $0$ for $\frac{\partial u_s}{\partial n}$ and $h$ for $n$ in Equation (IX).

  $\begin{array}{l}0=\frac{-g\sin \alpha }{\upsilon }h+C_1\\ C_1=\frac{g\sin \alpha }{\upsilon }h\end{array}$

Substitute $\frac{g\sin \alpha }{\upsilon }h$ for $C_1$ and $0$ for $C_2$ in Equation (X).

  $\begin{array}{c}{u}_s=\frac{-g\sin \alpha }{2\upsilon }{n}^2+\left(\frac{g\sin \alpha }{\upsilon }h\right)n+0\\ =\frac{g\sin \alpha }{2\upsilon }\left(2hn-n^2\right)\\ =\frac{g\sin \alpha }{2\upsilon }n\left(2h-n\right)\end{array}$   ....... (XI)

Substitute $\frac{\mu }{\rho }$ for $\upsilon$ in Equation (XI).

  $\begin{array}{c}{u}_s=\frac{g\sin \alpha }{2\left(\frac{\mu }{\rho }\right)}n\left(2h-n\right)\\ =\frac{\rho g\sin \alpha }{2\mu }n\left(2h-n\right)\end{array}$   ...... (XII)

Substitute $90°$ for $\alpha$ in Equation (XII).

  $\begin{array}{c}{u}_s=\frac{\rho g\sin \left(90°\right)}{2\mu }n\left(2h-n\right)\\ =\frac{\rho g\times 1}{2\mu }n\left(2h-n\right)\\ =\frac{\rho g}{2\mu }n\left(2h-n\right)\end{array}$  ......(XIII)

Write the expression for equation (V) of example 9-17.

  $w=\frac{\rho g}{2\mu }x\left(2h-x\right)$   ...... (XIV)

Here, velocity component is $w$ and position coordinate is $x$.

Since both sides of the Equation (XIII) are equal to Equation (XIV) which is equation (V) of example 9-17, therefore result is verified.

Let $n^{\ast }=\frac{n}{h}$ and $u_s^{\ast }=\frac{u_s\mu }{\rho g{h}^2}$ to convert Equation (XIII) in the Nondimensionalized form.

Substitute $h{n}^{\ast }$ for $n$ and $\frac{\rho g{h}^2{u}_s^{\ast }}{\mu }$ for $u_s$ in Equation (XIII).

  $\begin{array}{l}\frac{\rho g{h}^2{u}_s^{\ast }}{\mu }=\frac{\rho g\sin \alpha }{2\mu }\left(h{n}^{\ast }\right)\left(2h-h{n}^{\ast }\right)\\ \frac{\rho g{h}^2{u}_s^{\ast }}{\mu }=\frac{\rho g{h}^2\sin \alpha }{2\mu }\left(h{n}^{\ast }\right)\left(2h-h{n}^{\ast }\right)\\ u_s^{\ast }=\frac{n^{\ast }}{2}\left(2-n^{\ast }\right)\sin \alpha \end{array}$   ....... (XV)

Substitute $60°$ for $\alpha$, $0$ for $n\ast$ in equation (XV).

  $\begin{array}{c}{u}_s^{\ast }=\frac{0}{2}\left(2-0\right)\sin 60°\\ =0\times \sin 60°\\ =0\end{array}$

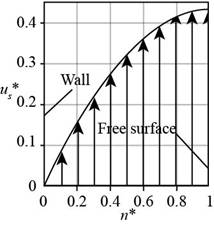
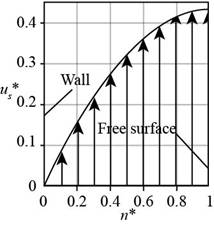
The following table represents different values of $u_s^{\ast }$ and $v$.

S.No.	$u_s^{\ast }\left(\alpha =60°\right)$	$n^{\ast }$
$1$	$0$	$0$
$2$	$0.1558$	$0.2$
$3$	$0.2771$	$0.4$
$4$	$0.3637$	$0.6$
$5$	$0.4156$	$0.8$
$6$	$0.433$	$1$

The following figure represents the plot of velocity profile.

  

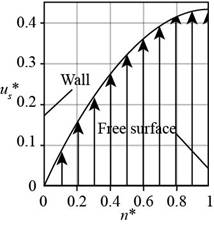
  Figure-(1)

Conclusion:

The velocity field is $\frac{\rho g\sin \alpha }{2\mu }n\left(2h-n\right)$.

The plot of velocity profile is shown in figure below.