
Determine the reactions at the suooorts, then draw the shear and moment diagrams. Assume the support at A is fixed and B is a roller, EI is constant.
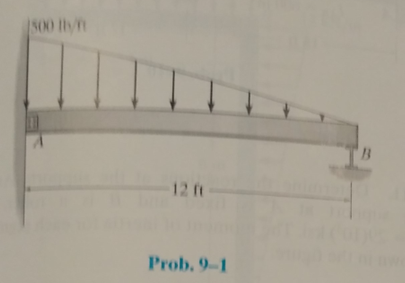
The reactions at the supports and to draw the shear and moment diagrams.
Answer to Problem 9.1P
The vertical reaction at support A is
The horizontal reaction at support A is
The reaction moment at support A is
The vertical reaction at support B is
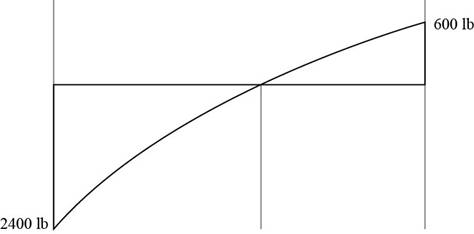
The shear diagram is shown below.
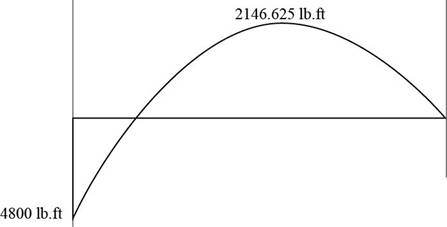
The moment diagram is shown below.
Explanation of Solution
Concept Used:
Write the expression for the net force balance in the vertical direction of the beam.
Here,
Write the expression for the net force balance in the horizontal direction in the beam.
Here,
Write the expression for the net moment about end
Here,
Calculations:
The free body diagram for the beam is shown below.
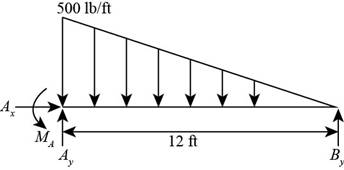
Figure (1)
Here, the vertical reaction at point
Calculate the support reactions using Equation (II).
The uniformly varying load is replaced by a concentrated force of magnitude
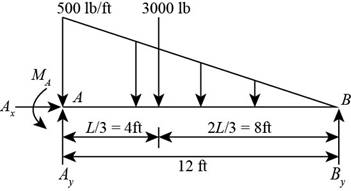
Figure (2)
Consider the moment at point A using Equation (III).
The displacement of the beam for the given load is shown below.
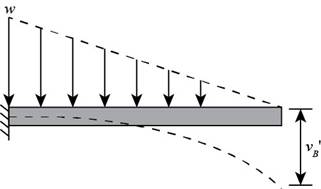
Figure (3)
Calculate the displacement of the beam for the given load.
Here, the displacement of the beam for the given load is
The displacement of the beam for the reaction at point B. is shown below.
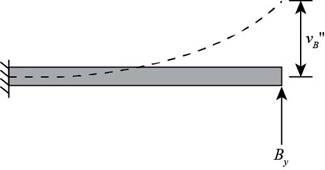
Calculate the displacement of the beam for the given load.
Here, the displacement of the beam for the reaction at point B is
Add Equation (VI) and Equation (VII) for the displacement values according to the compatibility condition.
Substitute
Calculate the vertical reaction at A using Equation (IV).
Substitute
Calculate the bending moment at A using Equation (V).
Substitute
Consider the beam as shown below.
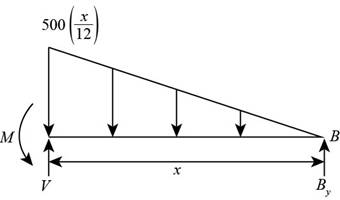
Figure (5)
Write the equation to determine the shear in the beam.
Calculate shear force at a distance
Substitute
Calculate shear force at a distance
Substitute
Calculate shear force at a distance
Substitute
Calculate shear force at a distance
Substitute
Calculate shear force at a distance
Substitute
Substitute
Write the expression for the bending moment.
Calculate moment at a distance
Substitute
Calculate moment at a distance
Substitute
Calculate moment at a distance
Substitute
Calculate moment at a distance
Substitute
Calculate moment at a distance
Substitute
Calculate moment at a distance
Substitute
Conclusion:
The vertical reaction at support A is
The horizontal reaction at support A is
The reaction moment at support A is
The vertical reaction at support B is
The shear diagram is shown below

Figure (6)
The moment diagram is shown below
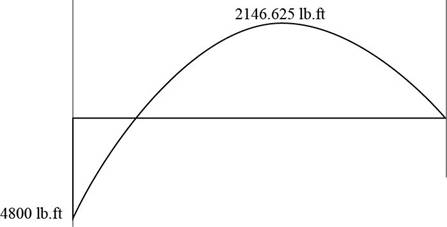
Figure (7)
Want to see more full solutions like this?
Chapter 9 Solutions
Structural Analysis, Student Value Edition
Additional Engineering Textbook Solutions
Concepts Of Programming Languages
Starting Out with Python (4th Edition)
Introduction To Programming Using Visual Basic (11th Edition)
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
Java: An Introduction to Problem Solving and Programming (8th Edition)
Modern Database Management
- steel designarrow_forwardSITUATION 1: A W250 x 131 is used as a column with an unbraced length of 8 m with respect to the x-x axis and 4 m with respect to the y-y axis. Assume an A36 steel member, pin-connected at the top and fixed at the bottom. Assume that the column is pin connected at mid-height. Use NSCP 2001 NSCP. Fy = 250 MPa. Properties of W250 x 131: A = 16,774 mm² d=274 mm bf=262 mm tf=25 mm tw = 16 mm Ix=222.268 x 10 mm ly = 74.505 x 10° mm* Effective Length Factors: Pinned at both ends, K = 1.0 Pinned at one end and fixed at the other, K = 0.8 1. What is the value of the slenderness ratio to be used for the column? 2. What is the nominal axial stress? 3. What is the design axial load? 1. 60.019 2. 206.543 MPa 3. 3118.091 kNarrow_forwardSITUATION 2: An 8-meter simply supported beam is to be loaded, in addition to its self-weight, a triangular distributed load that linearly increases from zero at the left support to 20 kN/m (dead) + 35 kN/m (live) at the right support. It is braced laterally at the end supports and at midspan. The details for the beam cross-section are given below. Use the LRFD provisions of NSCP 2015. W 540 mm x 150 kg/m: Area, A 19,225 mm² Depth, D = 540 mm Clear Distance between Flanges, h = 455 mm Flange width, bf=310 mm Flange thickness, tf = 20 mm Web thickness, tw 12.5 mm Elastic Section Modulus, Sx = 3.72 x 106 mm³ Plastic Section Modulus, Zx = 4.14 x 10 mm³ Torsional Constant, J = 2.04 x 10% mm* Distance between flange centroids, ho = 520 mm Radius of gyration along y-axis, ry = 72 mm Cb = 1.196 Effective radius of gyration, rts = 85 mm Yield Strength of Steel, Fy = 345 MPa Modulus of Elasticity, E=200 GPa 1. What is the ultimate moment capacity of the beam, in kN-m? 1. 1285.470 kN-marrow_forward
- SITUATION 4: A steel column W 300 x 203 kg/m is subjected to an axial load of 2670 kN. Unbraced length of column is 3m, and assume that the column is pinned at both ends, side sway prevented. Show your complete solution and box only the final answer. Properties of Column: Area, A = 25,740 mm² Depth, d=340 mm Flange thickness, tf = 32 mm Flange Width, bf=315 mm Web thickness, tw = 20 mm Ix = 5.16 x 10 mm² ly = 1.65 x 10° mm* Fy = 345.6 MPa 1. Determine the design strength (kN) of the column. 2. Determine the allowable strength (kN) of the column. 3. What is the value of the slenderness ratio to be used for the column? 1. 7223.401 kN 2. 4805.988 kN 3. 37.470arrow_forwardGive me a steel member design problems under combined axial and bending forces, using interaction equations, with complete solution and final answerarrow_forwardGive me compression member problems in steel design, including calculation of slenderness ratio and critical stress using Euler formula, with complete solution and answer.arrow_forward
- Give me flexural design problems of steel beams, including lateral-torsional buckling, and solve for nominal moment capacity, with step-by-step solution and answer.arrow_forwardGive me a sample tension member problems with staggered bolt holes where I calculate net area using the staggered hole formula, with complete solution and answer.arrow_forwardGive me a block shear failure problem involving a bolted steel plate, and solve for nominal strength, with detailed solution and answer.arrow_forward
- Give me a sample problems computing effective net area of a tension member with staggered holes, with full solution and answer. plsssarrow_forwardCan u pls give me sample problems on steel tension member design involving gross and net area, with complete solution and final answer. Note: I just needed to reviewarrow_forward(a) Determine the Nataf model for the joint PDF fxx, (xx) of the basic (physical) random variables X₁ and X, with marginal PDF's fx(x)=e, 0≤x (Exponential distribution) fx₁ (x2)=x2e-0.5x, 0≤x (Rayleigh distribution) and correlation coefficient Pxx=0.50 Note: Use Table 6 of paper by Liu and Der Kiureghian, 1986. (b) Generate a 3D surface plot and contour plot of the joint PDF fxx, (x,x) using Matlab or any other software of your choice. (c) What is the standard deviation of X2? (d) Construct a transformation from the physical X space (defined by random variables X, and X,) to the standard normal U space (defined by the statistically independent standard normal random variables (U, and U₂), i.e., U=T(X). Also describe the inverse transform X=T(U) and the Jacobian matrices J = ди θα and Ju Ox ди (e) According to the inverse transformation X = T¹ (U) and using Matlab, generate 1,000 samples from the Nataf joint PDF fxx, (x1,x2) derived in part (a). Start by generating samples of U using a…arrow_forward

 Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning Residential Construction Academy: House Wiring (M...Civil EngineeringISBN:9781285852225Author:Gregory W FletcherPublisher:Cengage Learning
Residential Construction Academy: House Wiring (M...Civil EngineeringISBN:9781285852225Author:Gregory W FletcherPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning





