Videos
(a)
What common fractional part of distance A is distance B.
Answer to Problem 55A
Explanation of Solution
Given information:
A figure is given as below.
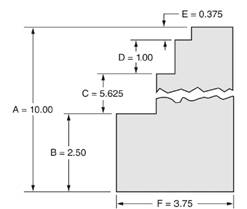
Calculation:
We have been given a figure as below.
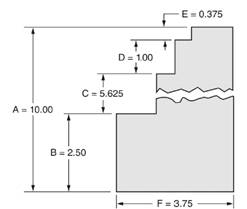
From above figure we observe that,
Distance A
So, ratio of distance B to distance A
i.e. ratio of distance B to distance A
i.e. ratio of distance B to distance A
Hence, we can say that
(b)
What common fractional part of distance A is distance C.
Answer to Problem 55A
Explanation of Solution
Given information:
A figure is given as below.
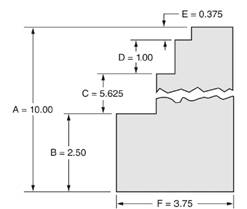
Calculation:
We have been given a figure as below.
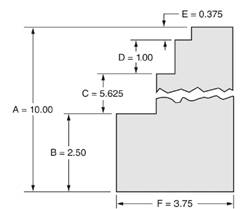
From above figure we observe that,
Distance A
So, ratio of distance C to distance A
i.e. ratio of distance C to distance A
i.e. ratio of distance C to distance A
Hence, we can say that
(c)
What common fractional part of distance A is distance D.
Answer to Problem 55A
Explanation of Solution
Given information:
A figure is given as below.
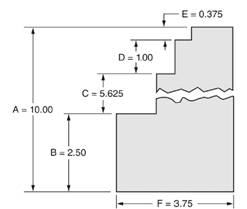
Calculation:
We have been given a figure as below.
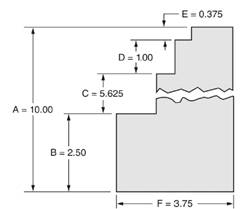
From above figure we observe that,
Distance A
So, ratio of distance D to distance A
i.e. ratio of distance D to distance A
i.e. ratio of distance D to distance A
Hence, we can say that
(d)
What common fractional part of distance A is distance E.
Answer to Problem 55A
Explanation of Solution
Given information:
A figure is given as below.
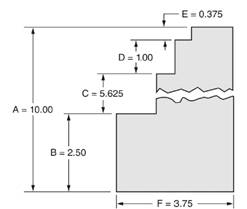
Calculation:
We have been given a figure as below.
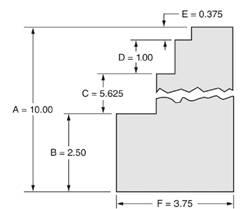
From above figure we observe that,
Distance A
So, ratio of distance E to distance A
i.e. ratio of distance E to distance A
i.e. ratio of distance E to distance A
Hence, we can say that
(e)
What common fractional part of distance A is distance F.
Answer to Problem 55A
Explanation of Solution
Given information:
A figure is given as below.
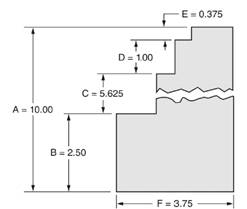
Calculation:
We have been given a figure as below.
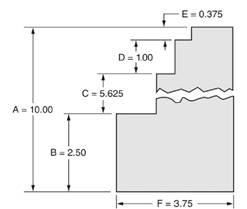
From above figure we observe that,
Distance A
So, ratio of distance F to distance A
i.e. ratio of distance F to distance A
i.e. ratio of distance F to distance A
Hence, we can say that
Want to see more full solutions like this?
Chapter 9 Solutions
Mathematics for Machine Technology
- 9. Establish the identity 1- 1+z+z² + 2n+1 ... +z" = 1- z (z1) and then use it to derive Lagrange's trigonometric identity: 1 1+ cos cos 20 +... + cos no = + 2 sin[(2n+1)0/2] 2 sin(0/2) (0 < 0 < 2л). Suggestion: As for the first identity, write S = 1+z+z² +...+z" and consider the difference S - zS. To derive the second identity, write z = eie in the first one.arrow_forward8. Prove that two nonzero complex numbers z₁ and Z2 have the same moduli if and only if there are complex numbers c₁ and c₂ such that Z₁ = c₁C2 and Z2 = c1c2. Suggestion: Note that (i≤ exp (101+0) exp (01-02) and [see Exercise 2(b)] 2 02 Ꮎ - = = exp(i01) exp(101+0) exp (i 01 - 02 ) = exp(102). i 2 2arrow_forwardnumerical anaarrow_forward
- 2) Consider the matrix M = [1 2 3 4 5 0 2 3 4 5 00345 0 0 0 4 5 0 0 0 0 5 Determine whether the following statements are True or False. A) M is invertible. B) If R5 and Mx = x, then x = 0. C) The last row of M² is [0 0 0 0 25]. D) M can be transformed into the 5 × 5 identity matrix by a sequence of elementary row operations. E) det (M) 120 =arrow_forward3) Find an equation of the plane containing (0,0,0) and perpendicular to the line of intersection of the planes x + y + z = 3 and x y + z = 5. -arrow_forward1) In the xy-plane, what type of conic section is given by the equation - √√√(x − 1)² + (y − 1)² + √√√(x + 1)² + (y + 1)² : - = 3?arrow_forward
- 3) Let V be the vector space of all functions f: RR. Prove that each W below is a subspace of V. A) W={f|f(1) = 0} B) W = {f|f(1) = ƒ(3)} C) W={ff(x) = − f(x)}arrow_forwardTranslate the angument into symbole from Then determine whether the argument is valid or Invalid. You may use a truth table of, it applicable compare the argument’s symbolic form to a standard valid or invalid form. pot out of bed. The morning I did not get out of bed This moring Mat woke up. (1) Cidt the icon to view tables of standard vald and braild forms of arguments. Let prepresent."The morning Must woke up "and let a represent “This morning I got out of bed.” Seled the cared choice below and II in the answer ber with the symbolic form of the argument (Type the terms of your expression in the same order as they appear in the original expression) A. The argument is valid In symbolic form the argument is $\square $ B. The angunent is braid In symbolic form the argument is $\square $arrow_forwardWrite the prime factorization of 8. Use exponents when appropriate and order the factors from least to greatest (for example, 22.3.5). Submitarrow_forward
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning