
Concept explainers
A particle moves in the xy plane (Fig. P9.30) from the origin to a point having coordinates x = 7.00 m and y = 4.00 m under the influence of a force given by
- a. What is the work done on the particle by the force F if it moves along path 1 (shown in red)?
- b. What is the work done on the particle by the force F if it moves along path 2 (shown in blue)?
- c. What is the work done on the particle by the force F if it moves along path 3 (shown in green)?
- d. Is the force F conservative or nonconservative? Explain.
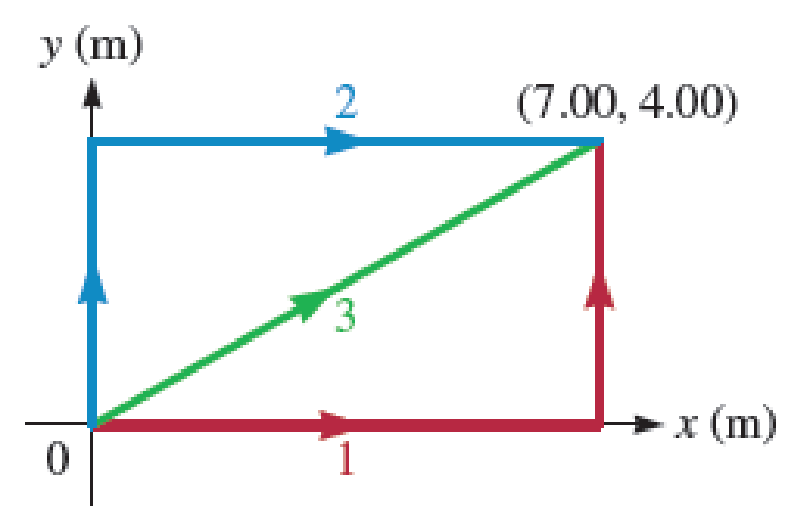
FIGURE P9.30
In each case, the work is found using the integral of
(a) The work done along path 1, we first need to integrate along
Performing the dot products, we get
Along the first part of this path, y = 0 therefore the first integral equals zero. For the second integral, x is constant and can be pulled out of the integral, and we can evaluate dy.
(b) The work done along path 2 is along
Performing the dot product, we get:
Along the first part of this path, x = 0. Therefore, the first integral equals zero. For the second integral, y is constant and can be pulled out of the integral, and we can evaluate dx.
(c) To find the work along the third path, we first write the expression for the work integral.
At first glance, this appears quite simple, but we can’t integrate
Now, use equation (2) in (1) to express each integral in terms of only one variable.
We can determine the tangent of the angle, which is constant (the angle is the angle of the line with respect to the horizontal).
Insert the value of the tangent and solve the integrals.
(d) Since the work done is not “path-independent”, this is
Figure P9.30ANS
(a)
The work done on the particle by the force
Answer to Problem 30PQ
The work done on the particle by the force
Explanation of Solution
The path 1 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is
Write the expression for the work done by a force.
Here,
The path 1 of the particle consist of two parts. Motion from
Use the force vector along with the limits of integration and perform the integration (represent the work done along path 1 as
Perform the dot product to reduce the integral (II).
Along the first part of the path 1,
Conclusion:
Therefore, the work done on the particle by the force
(b)
The work done on the particle by the force
Answer to Problem 30PQ
The work done on the particle by the force
Explanation of Solution
The path 2 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is
Equation (I) gives the expression for the work done by a force.
The path 2 of the particle consist of two parts. Motion from
Use the force vector along with the limits of integration and perform the integration (represent the work done along path 2 as
Perform the dot product to reduce the integral (IV).
Along the first part of the path 2,
Conclusion:
Therefore, the work done on the particle by the force
(c)
The work done on the particle by the force
Answer to Problem 30PQ
The work done on the particle by the force
Explanation of Solution
The path 3 followed by the particle is given in Figure P9.30. Given that the coordinate of the final position of the particle is
Equation (I) gives the expression for the work done by a force.
Write equation (I) in terms of
Use the
The path 3 of the particle starts from
Here, both
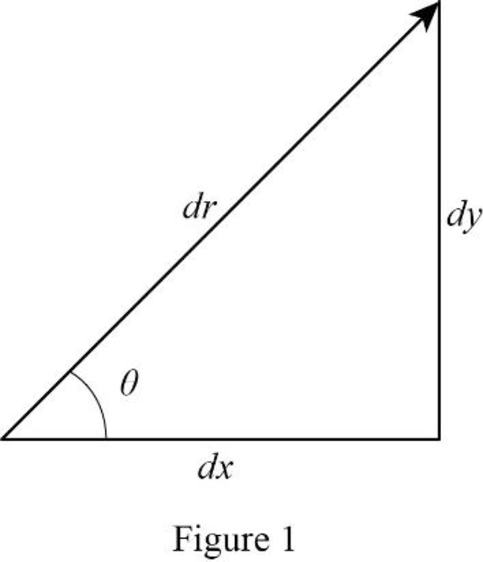
Write the expression relating
Solve equation (IX) for
Solve equation (IX) for
Use equation (X) and (XI) in (VIII).
Compute
Use equation (XIII) in (XII) and perform the integral.
Conclusion:
Therefore, the work done on the particle by the force
(d)
Whether the force
Answer to Problem 30PQ
The force
Explanation of Solution
From part (a), (b) and (c) it is found that the work done by the force
Conclusion:
Therefore, the force
Want to see more full solutions like this?
Chapter 9 Solutions
Physics For Scientists And Engineers: Foundations And Connections, Extended Version With Modern Physics
- Show that the units 1 v2/Q = 1 W, as implied by the equation P = V²/R. Starting with the equation P = V²/R, we can get an expression for a watt in terms of voltage and resistance. The units for voltage, V, are equivalent to [? v2 v2 A, are equivalent to J/C ✓ X . Therefore, 1 = 1 = 1 A V1 J/s Ω V-A X = 1 W. . The units for resistance, Q, are equivalent to ? The units for current,arrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forward
- According to the provided information answer the question accorrding to grade 11 physics Jerry has decided to give up his part-time job for a new career, cat-burglar! Jerry loves the idea of dressing up like a cat all day and of course the chance of meeting Cat Woman! On Jerry's first "job" he figures out his escape plan. He travels 3.0 km south for 15 minutes and then 8.0 km west for 1.5 hours before reaching his house. Draw a sketch diagram of the path he took with all the appropriate labels.arrow_forwardPlease solve and answer all parts of the question correctly please. Thank you!!arrow_forwardPlease solve and answer this question correctly please. Thank you!!arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





