
Find maximum positive shear and bending moment at point B due to the series of four moving concentrated loads
Explanation of Solution
Calculation:
Apply a 1 k unit moving load at a distance of x from left end A.
Sketch the free body diagram of beam as shown in Figure 1.
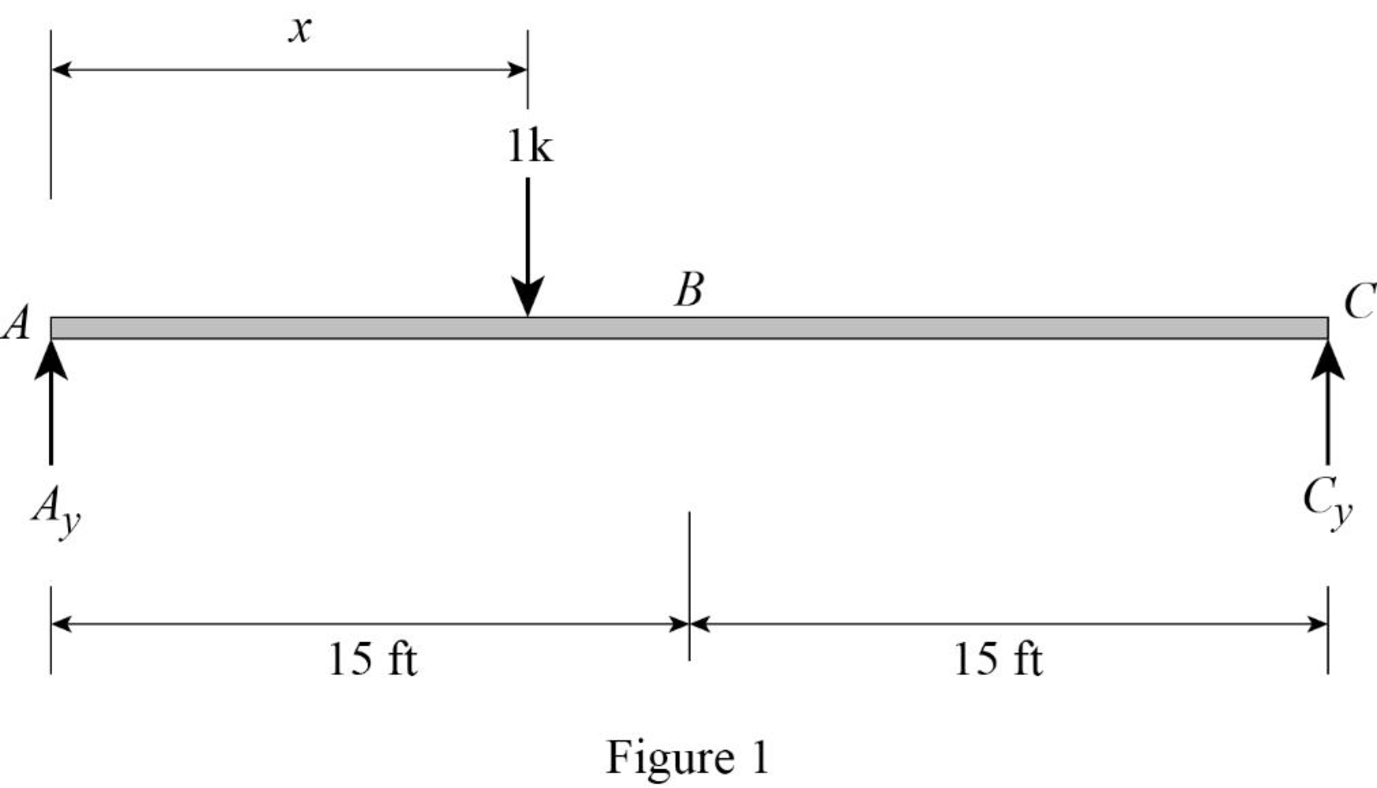
Refer Figure 1.
Find the equation of support reaction
Take moment about point C.
Consider moment equilibrium at point C.
Consider clockwise moment as positive and anticlockwise moment as negative.
Sum of moment at point C is zero.
Find the equation of support reaction
Apply vertical equilibrium equation of forces.
Consider upward force as positive
Substitute
Influence line for shear at B.
Find the equation of shear force at B of portion AB
Sketch the free body diagram of the section AB as shown in Figure 2.
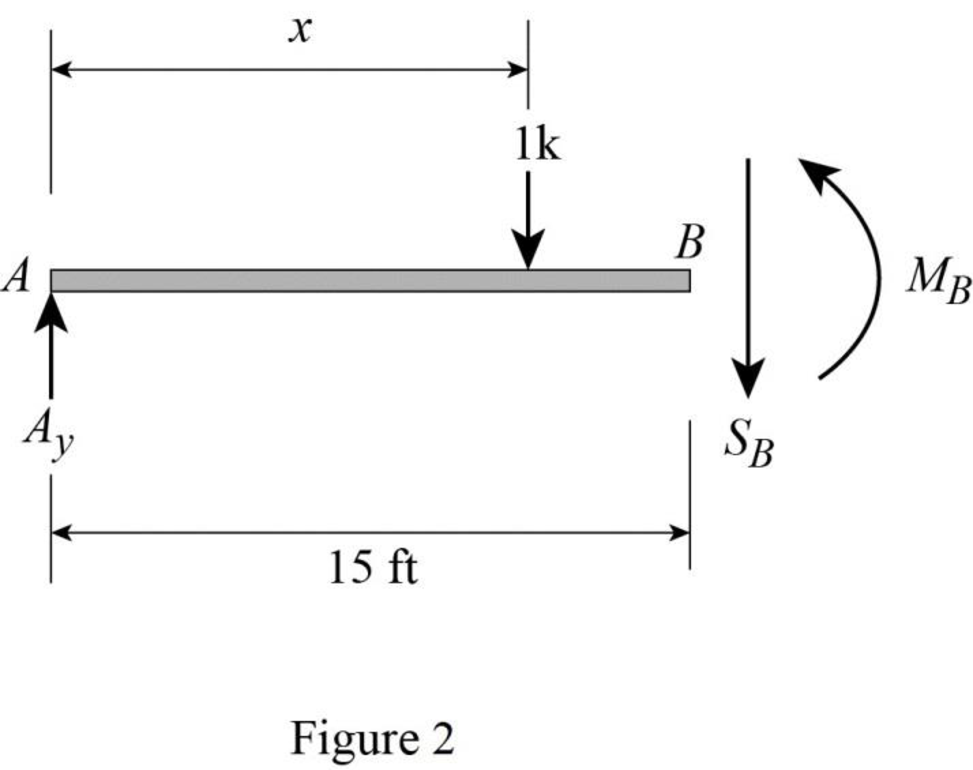
Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear force at B of portion BC
Sketch the free body diagram of the section BC as shown in Figure 3.
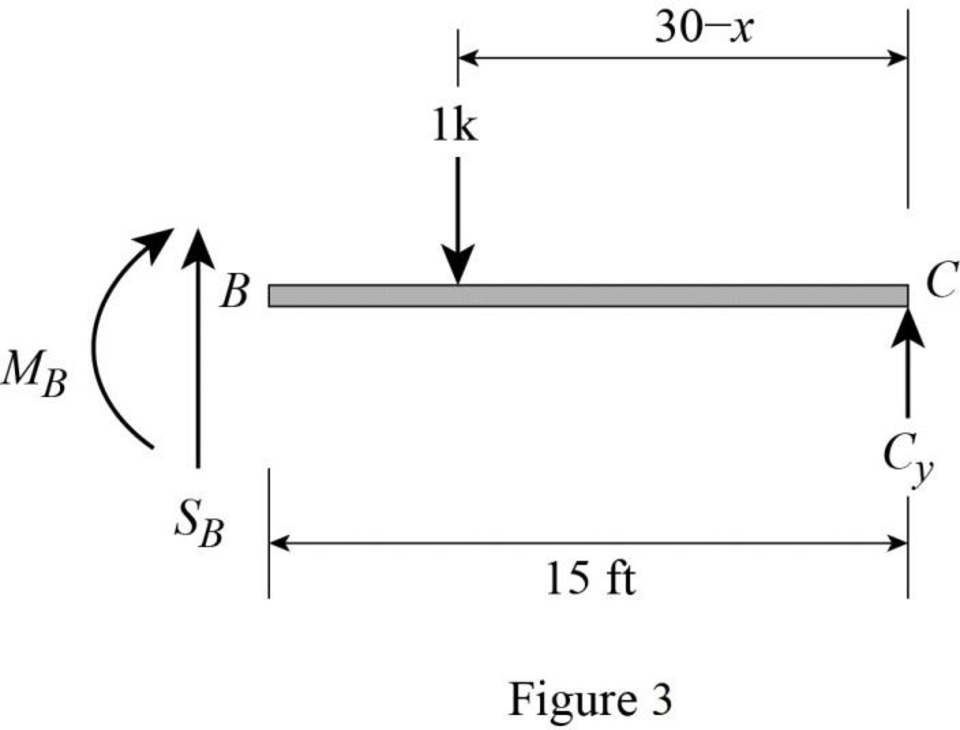
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of shear force at various points of x using the Equations (3) and (4) and summarize the value as in Table 1.
| x | |
| 0 | 1 |
| 30 | 0 |
Draw the influence lines for the shear force at point B using Table 1 as shown in Figure 4.
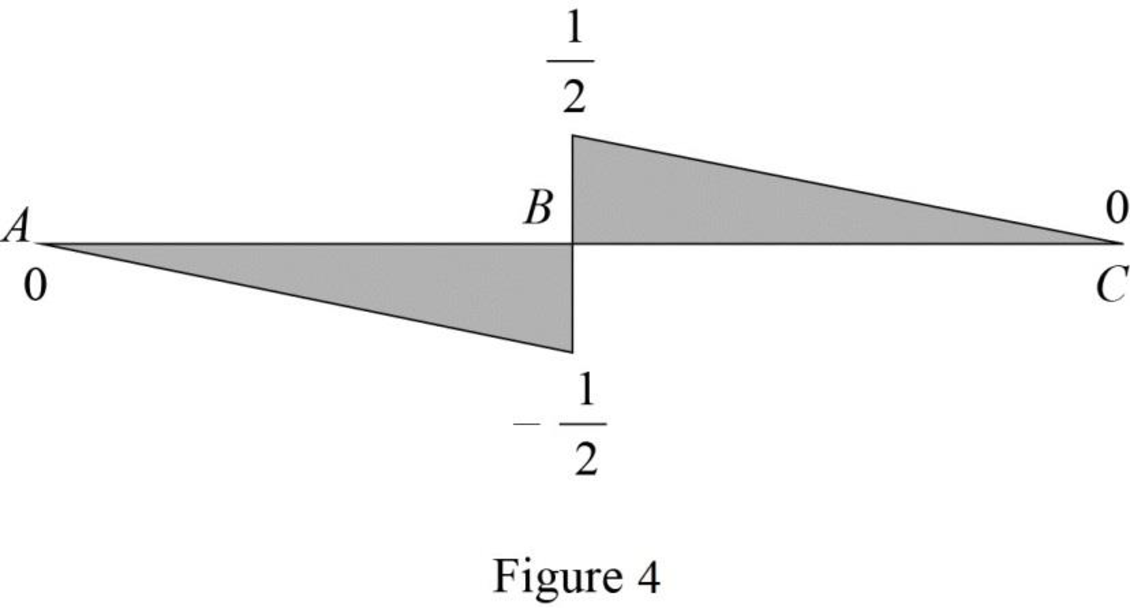
Refer Figure 4.
Find the slope
Here,
Substitute 15 ft for
Find the slope
Here,
Substitute 15 ft for
Sketch the loading position as shown in Figure 5.
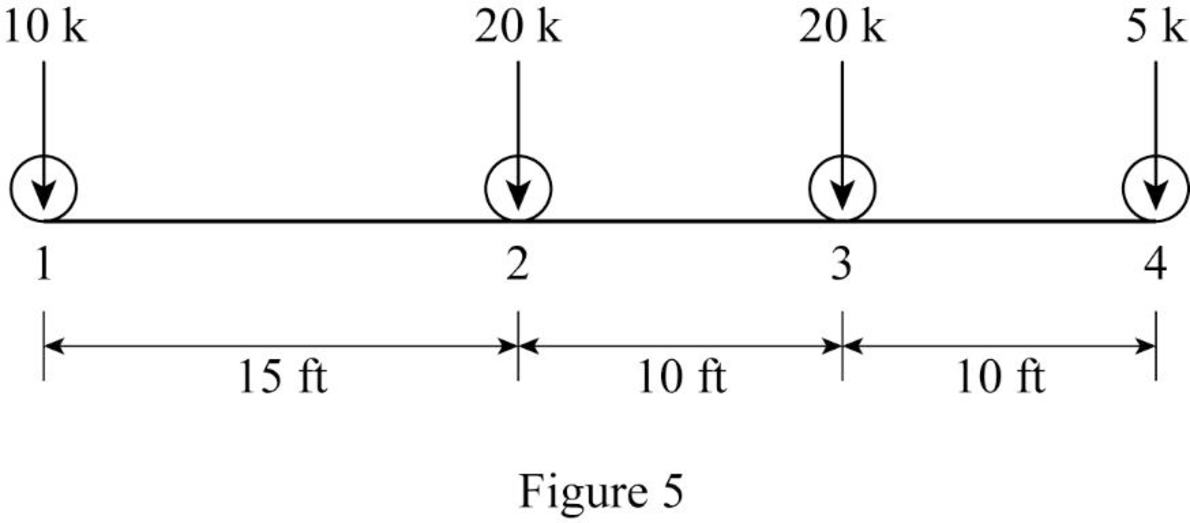
Find the maximum positive shear force at B.
Sketch the loading position on the beam when the load 1 placed at just right of B as shown in Figure 6.
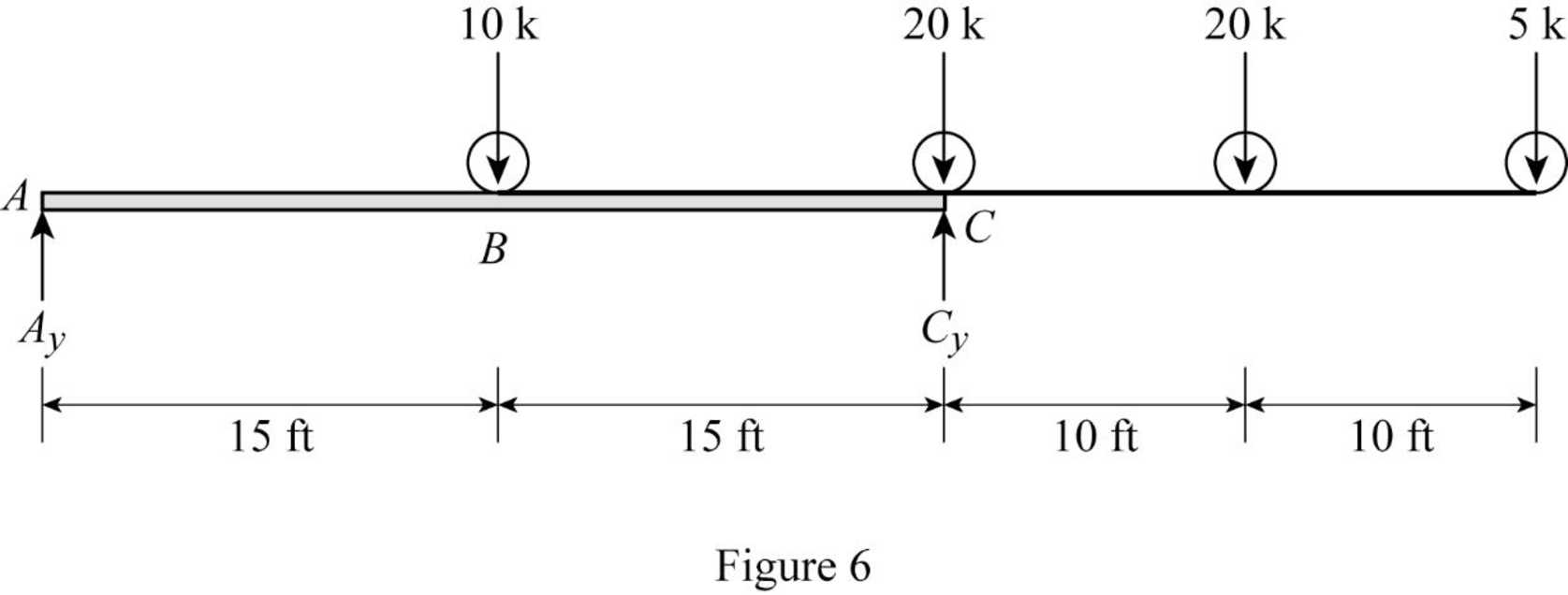
Refer Figure 6.
Find the shear force at B when the load 1 placed at just right of B.
Substitute 15 ft for
Sketch the loading position on the beam when the load 2 placed at just right of B as shown in Figure 7.
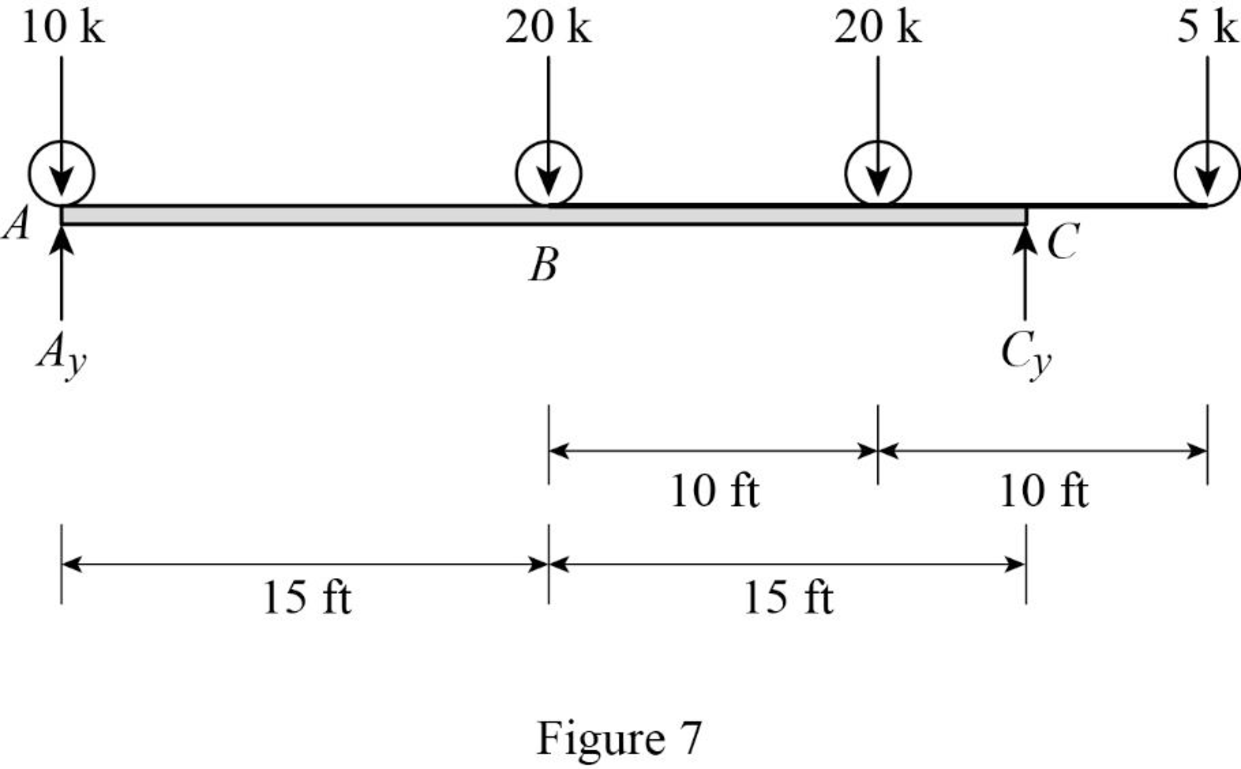
Refer Figure 7.
Find the shear force at B when the load 2 placed at just right of B.
Substitute 15 ft for
Sketch the loading position on the beam when the load 3 placed at just right of B as shown in Figure 8.
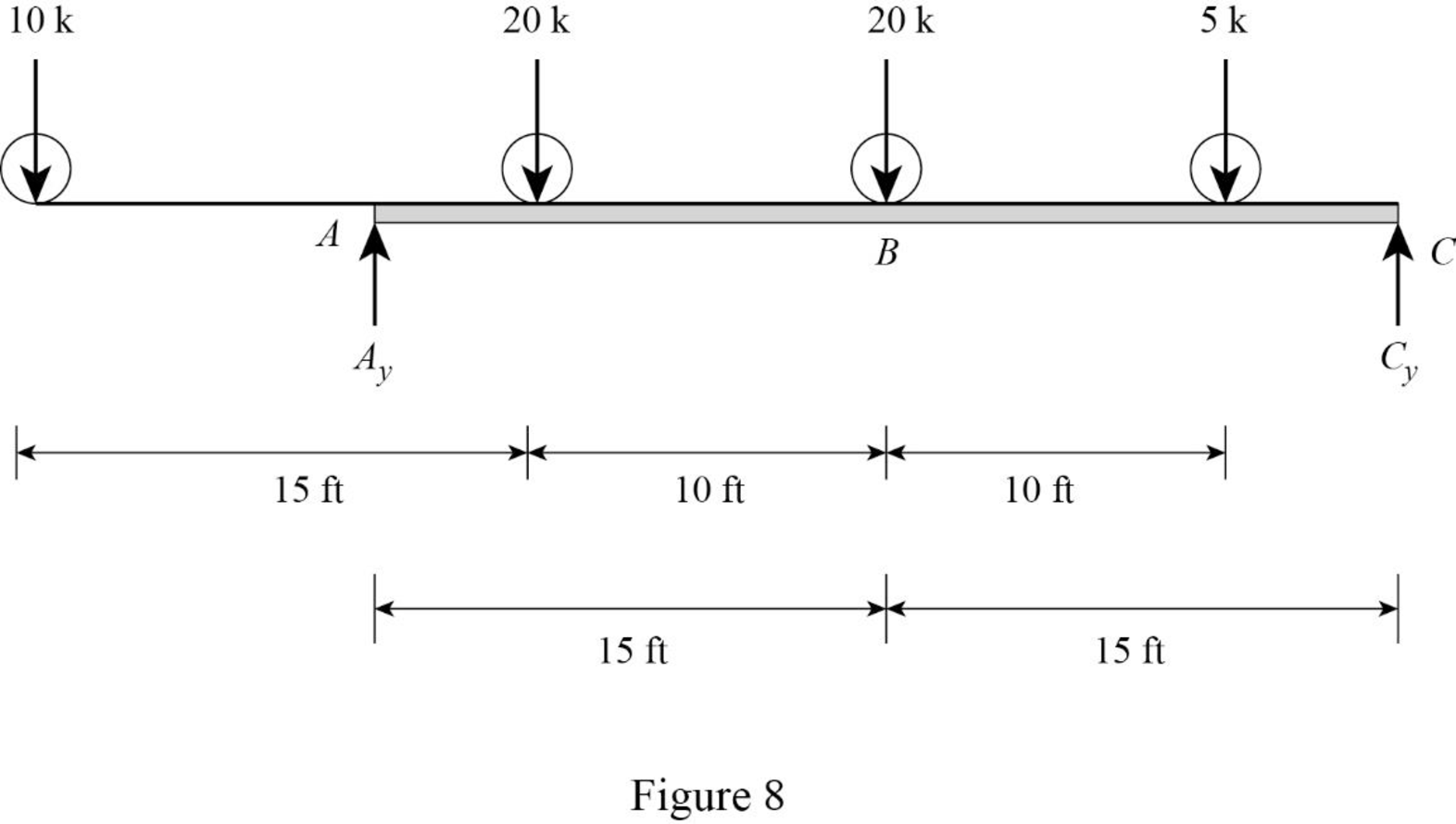
Refer Figure 8.
Find the shear force at B when the load 3 placed at just right of B.
Substitute 15 ft for
Sketch the loading position on the beam when the load 4 placed at just right of B as shown in Figure 9.
Refer Figure 9.
Find the shear force at B when the load 3 placed at just right of B.
Substitute 15 ft for
Maximum positive shear force at B as follows.
The maximum positive shear at B is the maximum of
Therefore, the maximum positive shear at point B is
Influence line for moment at B.
Refer Figure 2.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the equation of moment at B of portion AB
Substitute
Refer Figure 3.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the equation of moment at B of portion BC
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of moment at various points of x using the Equations (5) and (6) and summarize the value as in Table 2.
| x | |
| 0 | 0 |
| 30 | 0 |
Draw the influence lines for the moment at point B using Table 2 as shown in Figure 10.

Refer Figure 9.
The slope of portion AB and BC is same.
Find the slope
Here,
Substitute 15 ft for
Find the maximum positive bending moment at B.
Refer Figure 6.
Find the bending moment at B when the load 1 placed at just right of B.
Substitute 15 ft for
Refer Figure 7.
Find the bending moment at B when the load 2 placed at just right of B.
Substitute 15 ft for
Refer Figure 8.
Find the bending moment at B when the load 3 placed at just right of B.
Substitute 15 ft for
Refer Figure 9.
Find the bending moment at B when the load 1 placed at just right of B.
Substitute 15 ft for
Maximum positive bending moment at B as follows.
The maximum positive bending moment at B is the maximum of
Therefore, the maximum positive bending moment at point B is
Want to see more full solutions like this?
- Why is it important for construction project managers to be flexible when dealing with the many variable factors that pop up in a project?arrow_forwardWhat are some reasons for why a company would accelerate a construction project?arrow_forwardFor the design of a shallow foundation, given the following: Soil: ' = 20° c' = 52 kN/m² Unit weight, y = 15 kN/m³ Modulus of elasticity, E, = 1400 kN/m² Poisson's ratio, μs = 0.35 Foundation: L=2m B=1m Df = 1 m Calculate the ultimate bearing capacity. Use the equation: 1 - qu = c' NcFcs Fcd Fcc +qNqFqsFqdFqc + ½√BN√Fãs F√dƑxc 2 For '=20°, Nc = 14.83, N₁ = 6.4, and N₁ = 5.39. (Enter your answer to three significant figures.) qu = kN/m²arrow_forward
- A 2.0 m wide strip foundation carries a wall load of 350 kN/m in a clayey soil where y = 15 kN/m³, c' = 5.0 kN/m² and ' = 23°. The foundation depth is 1.5 m. For ' = 23°: Nc = 18.05; N₁ = 8.66; Ny = = = 8.20. Determine the factor of safety using the equation below. qu= c' NcFcs FcdFci+qNqFqsFq 1 F + gd. 'qi 2 ·BN√· FF γί Ysyd F (Enter your answer to three significant figures.) FS =arrow_forward2P -1.8 m- -1.8 m- -B Wo P -1.8 m- Carrow_forwardPart F: Progressive activity week 7 Q.F1 Pick the rural location of a project site in Victoria, and its catchment area-not bigger than 25 sqkm, and given the below information, determine the rainfall intensity for ARI 5, 50, 100 year storm event. Show all the details of the procedure. Each student must propose different length of streams and elevations. Use fig below as a sample only. Pt. E-nt 950 200 P: D-40, PC-92.0 300m 300m 000m PL.-02.0 500m HI-MAGO PLA-M 91.00 To be deemed satisfactory the solution must include: Q.F1.1.Choice of catchment location Q.F1.2. A sketch displaying length of stream and elevation Q.F1.3. Catchment's IFD obtained from the Buro of Metheorology for specified ARI Q.F1.4.Calculation of the time of concentration-this must include a detailed determination of the equivalent slope. Q.F1.5.Use must be made of the Bransby-Williams method for the determination of the equivalent slope. Q.F1.6.The graphical display of the estimation of intensities for ARI 5,50, 100…arrow_forward
- I need help finding: -The axial deflection pipe in inches. -The lateral deflection of the beam in inches -The total deflection of the beam like structure in inches ?arrow_forwardA 2.0 m wide strip foundation carries a wall load of 350 kN/m in a clayey soil where y = 17 kN/m³, c' = 5.0 kN/m² and 23°. The foundation depth is 1.5 m. For o' = 23°: Nc = 18.05; N = 8.66; N = 8.20. Determine the factor of safety using the equation below. 1 qu = c' NcFcs Fed Fci +qNqFqs FqdFqi + ½ BN F√s 1 2 (Enter your answer to three significant figures.) s Fyd Fi FS =arrow_forward1.2 m BX B 70 kN.m y = 16 kN/m³ c' = 0 6'-30° Water table Ysat 19 kN/m³ c' 0 &' = 30° A square foundation is shown in the figure above. Use FS = 6, and determine the size of the foundation. Use the Prakash and Saran theory (see equation and figures below). Suppose that F = 450 kN. Qu = BL BL[c′Nc(e)Fcs(e) + qNg(e)Fcs(e) + · 1 YBN(e) F 2 7(e) Fra(e)] (Enter your answer to two significant figures.) B: m Na(e) 60 40- 20- e/B=0 0.1 0.2 0.3 .0.4 0 0 10 20 30 40 Friction angle, ' (deg) Figure 1 Variation of Na(e) with o' Ny(e) 60 40 20 e/B=0 0.3 0.1 0.2 0.4 0 0 10 20 30 40 Friction angle, ' (deg) Figure 2 Variation of Nye) with o'arrow_forward
- K/S 46. (O المهمات الجديدة 0 المنتهية 12 المغـ ۱۱:۰۹ search ليس لديك اي مهمات ☐ ○ ☑arrow_forwardI need help setti if this problem up and solving. I keep doing something wrong.arrow_forward1.0 m (Eccentricity in one direction only)=0.15 m Call 1.5 m x 1.5m Centerline An eccentrically loaded foundation is shown in the figure above. Use FS of 4 and determine the maximum allowable load that the foundation can carry if y = 18 kN/m³ and ' = 35°. Use Meyerhof's effective area method. For '=35°, N = 33.30 and Ny = 48.03. (Enter your answer to three significant figures.) Qall = kNarrow_forward
