
Find the maximum positive shear and bending moment at point B.
Answer to Problem 13P
The maximum positive shear at point B is
The maximum positive bending moment at point B is
Explanation of Solution
Calculation:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of beam as shown in Figure 1.
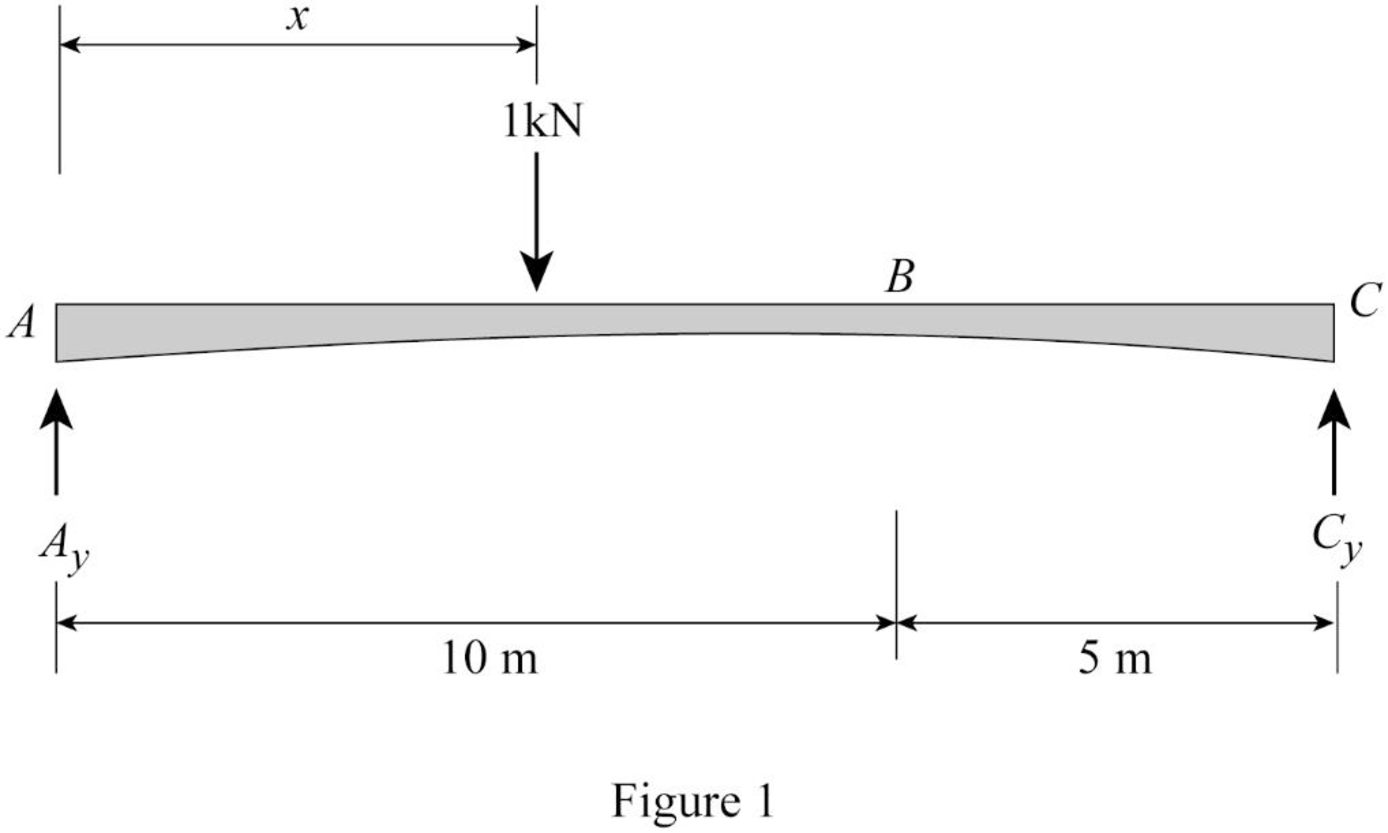
Refer Figure 1.
Find the equation of support reaction
Take moment about point C.
Consider moment equilibrium at point C.
Consider clockwise moment as positive and anticlockwise moment as negative.
Sum of moment at point C is zero.
Find the equation of support reaction
Apply vertical equilibrium equation of forces.
Consider upward force as positive
Substitute
Influence line for shear at point B.
Find the equation of shear force at B of portion AB
Sketch the free body diagram of the section AB as shown in Figure 2.
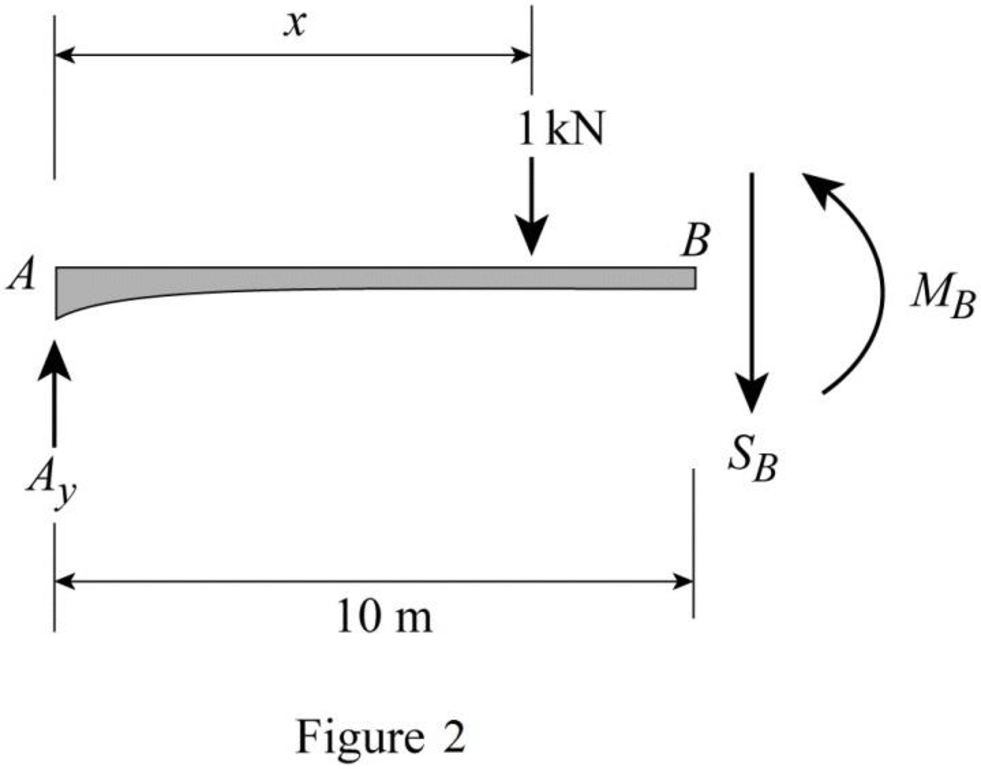
Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear force at B of portion BC
Sketch the free body diagram of the section BC as shown in Figure 3.
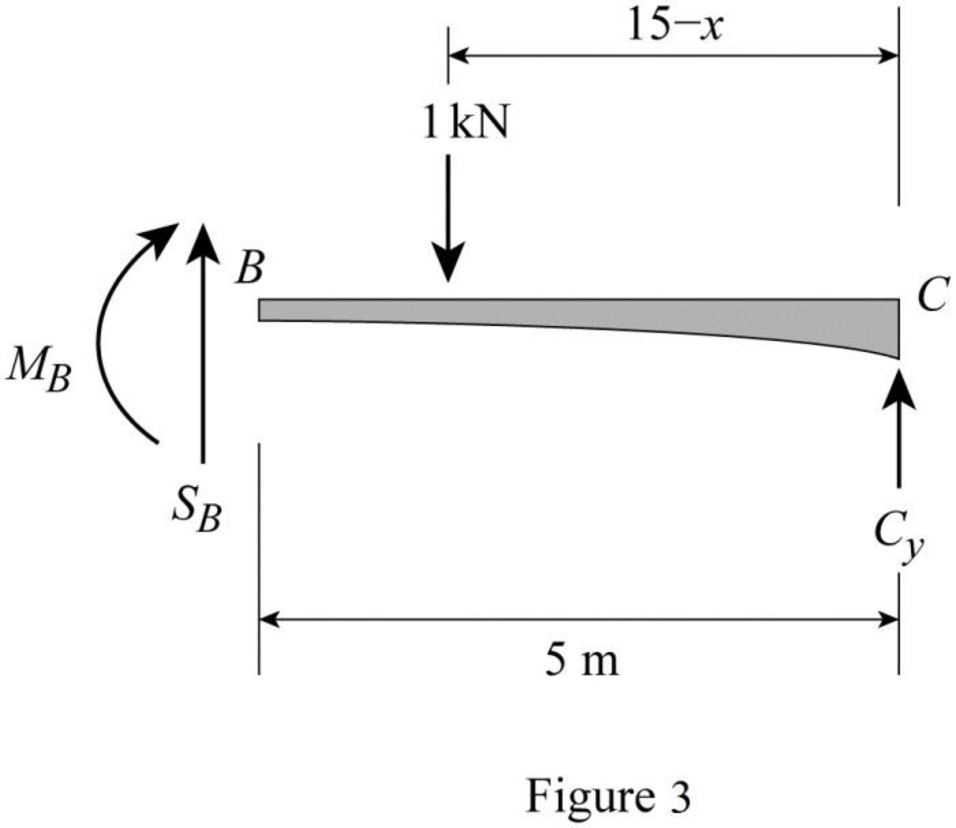
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of shear force at various points of x using the Equations (3) and (4) and summarize the value as in Table 1.
| x | |
| 0 | 0 |
| 16 | 0 |
Draw the influence lines for the shear force at point B using Table 1 as shown in Figure 4.
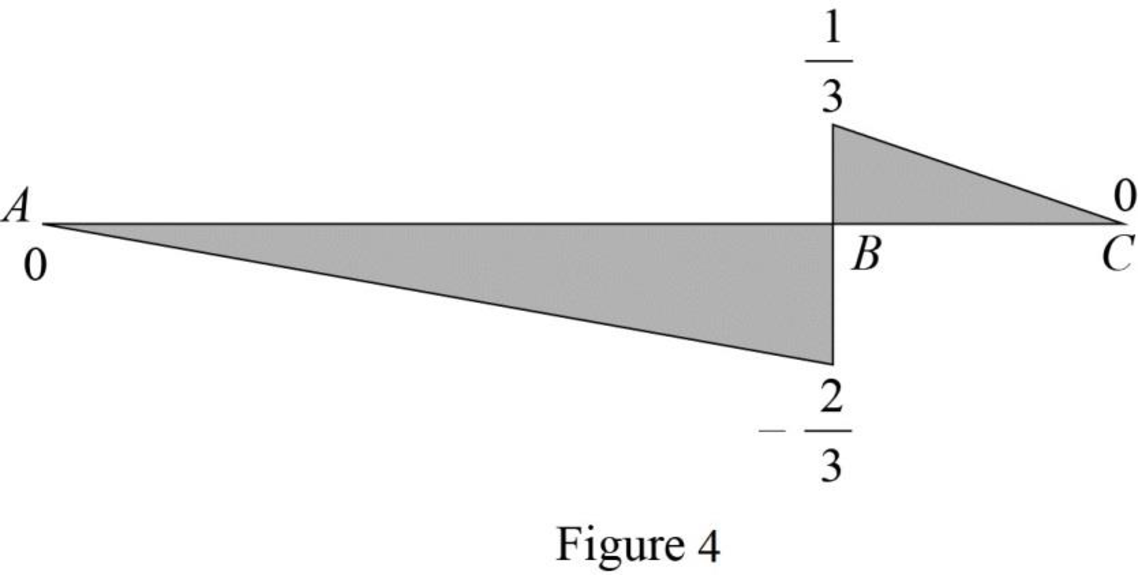
Refer Figure 4.
Find the slope
Here,
Substitute 10 m for
Find the slope
Here,
Substitute 5 m for
Sketch the loading position as shown in Figure 5.
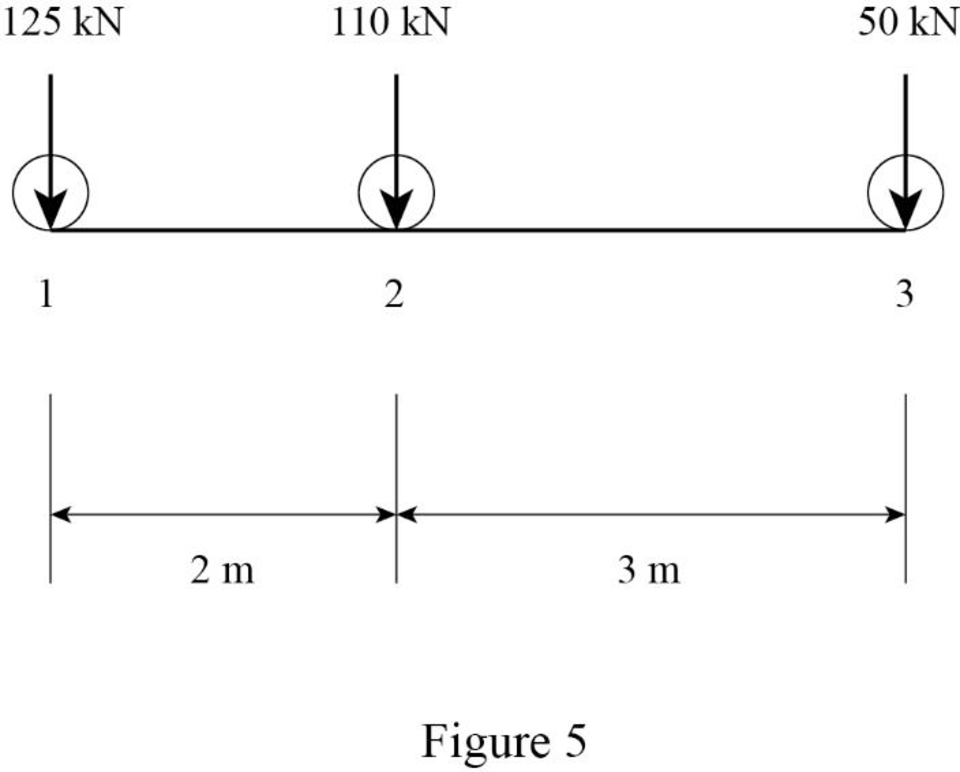
Find the maximum positive shear force at B.
Sketch the loading position on the beam when the load 1 placed at just right of B as shown in Figure 6.
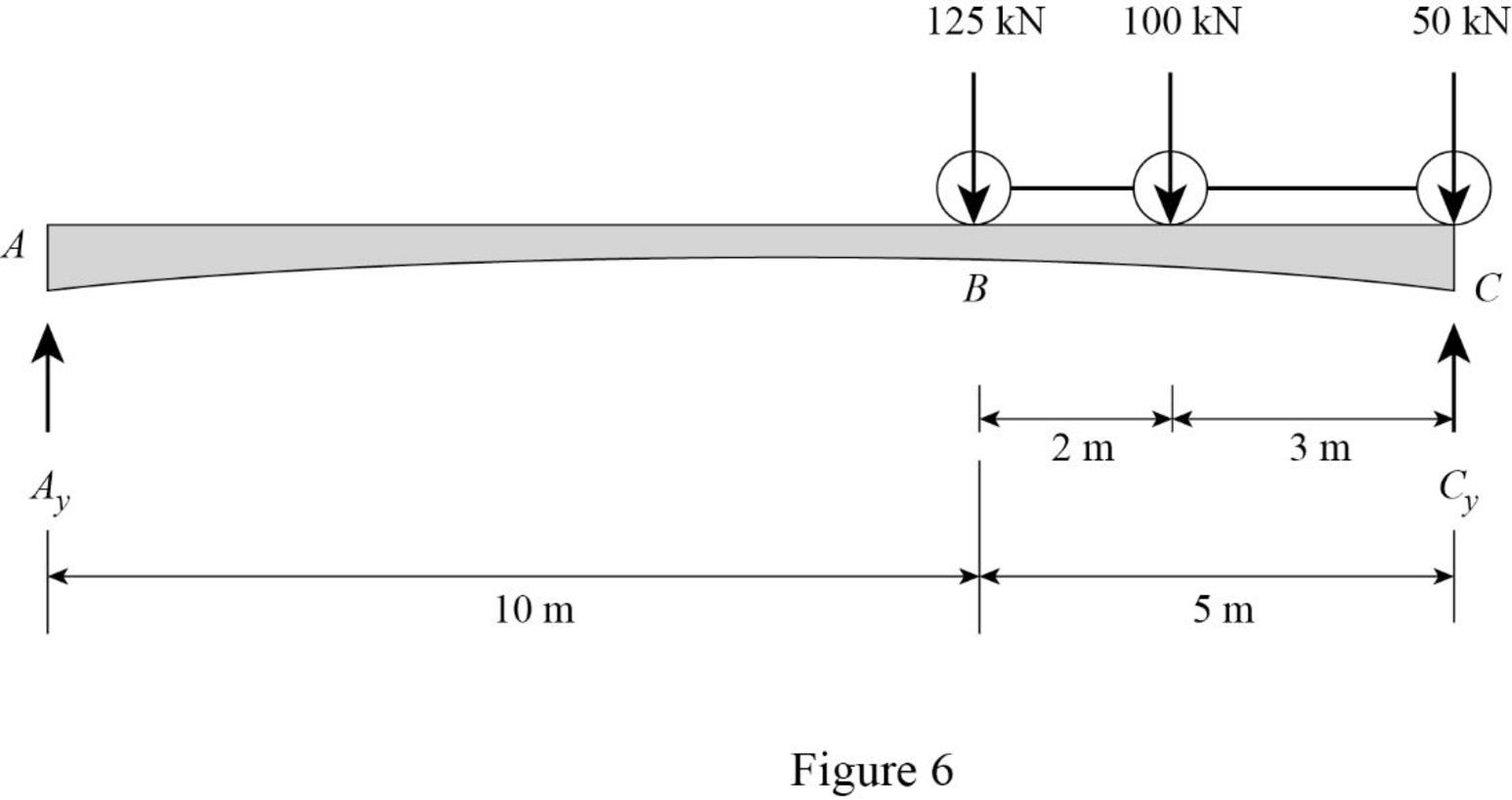
Refer Figure 6.
Find the shear force at B when the load 1 placed at just right of B.
Substitute 5 m for
Sketch the loading position on the beam when the load 2 placed at just right of B as shown in Figure 7.
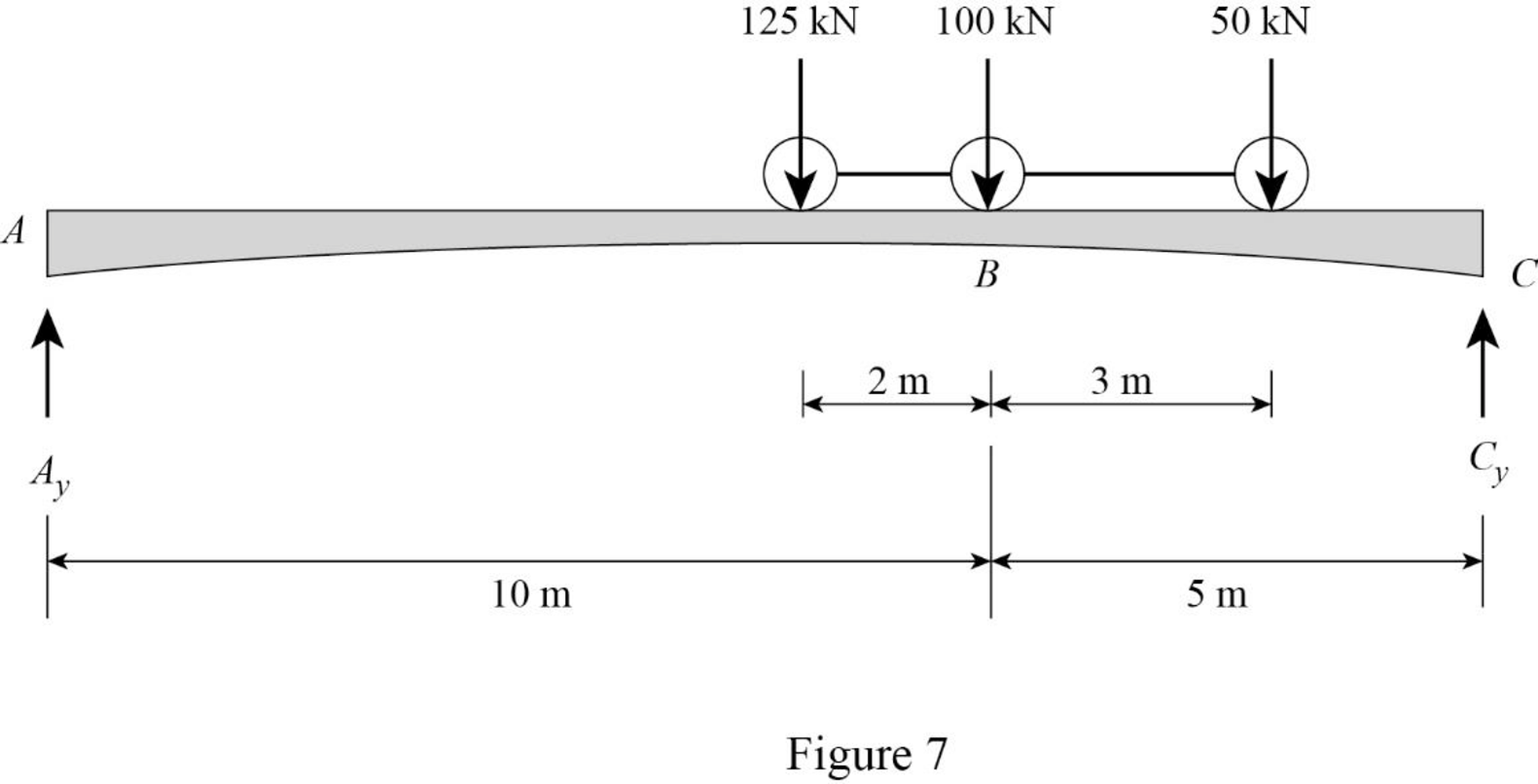
Refer Figure 7.
Find the shear force at B when the load 2 placed at just right of B.
Substitute 10 m for
Sketch the loading position on the beam when the load 3 placed at just right of B as shown in Figure 8.
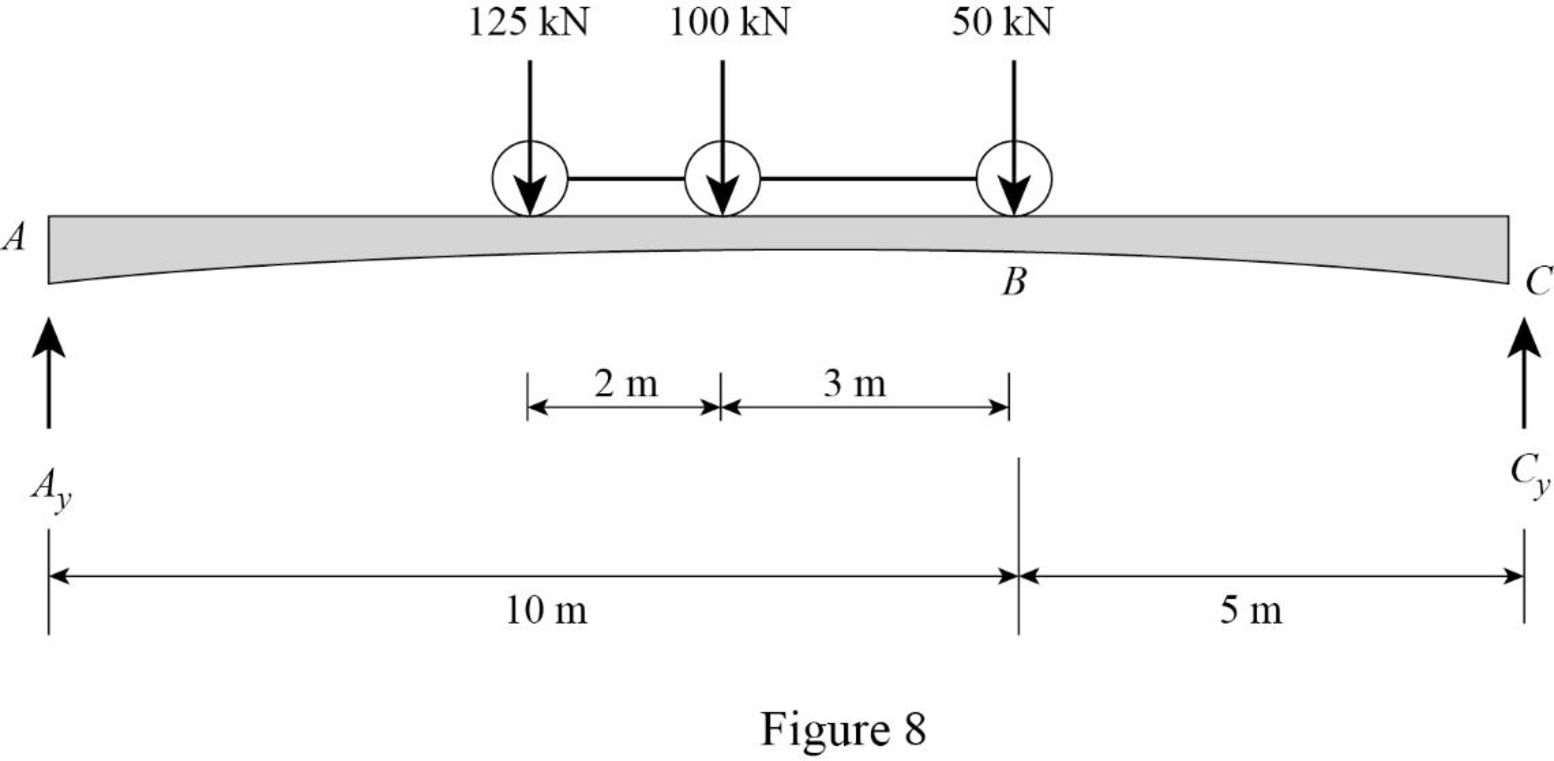
Refer Figure 8.
Find the shear force at B when the load 3 placed at just right of B.
Substitute 10 m for
Maximum positive shear force at B as follows.
The maximum positive shear at B is the maximum of
Therefore, the maximum positive shear at point B is
Influence line for moment at B.
Refer Figure 2.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the equation of moment at B of portion AB
Substitute
Refer Figure 3.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the equation of moment at B of portion BC
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of moment at various points of x using the Equations (5) and (6) and summarize the value as in Table 2.
| x | |
| 0 | 0 |
| 10 | |
| 15 | 0 |
Draw the influence lines for the moment at point B using Table 2 as shown in Figure 9.
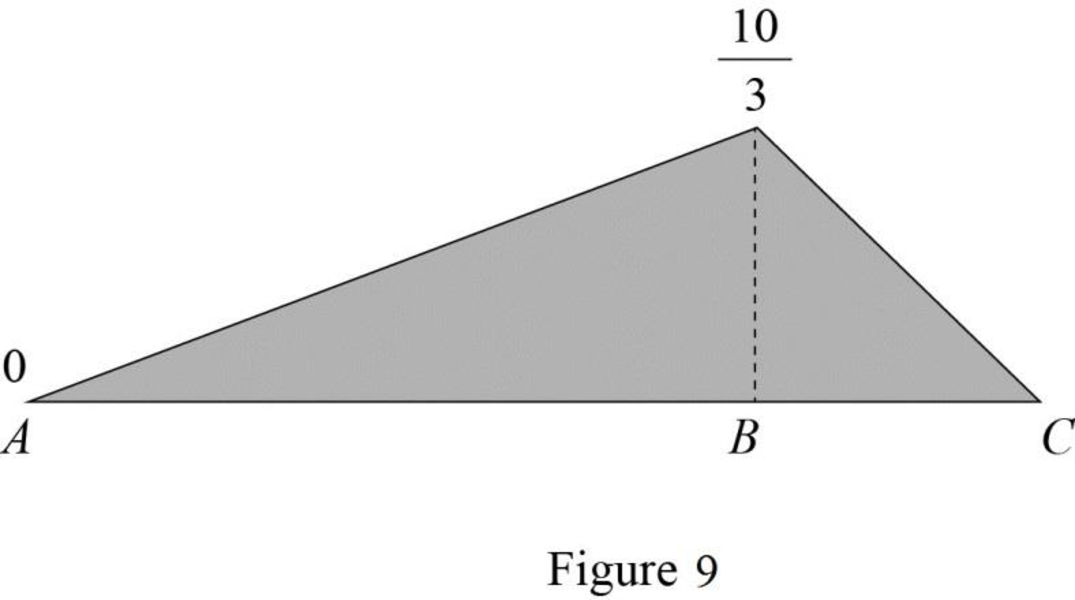
Refer Figure 9.
Find the slope
Here,
Substitute 10 m for
Find the slope
Here,
Substitute 5 m for
Find the maximum positive bending moment at B.
Refer Figure 6.
Find the bending moment at B when the load 1 placed at just right of B.
Substitute 5 m for
Refer Figure 7.
Find the bending moment at B when the load 2 placed at just right of B.
Substitute 10 m for
Refer Figure 8.
Find the bending moment at B when the load 3 placed at just right of B.
Substitute 10 m for
Maximum positive bending moment at B. as follows.
The maximum positive bending moment at B is the maximum of
Therefore, the maximum positive bending moment at point B is
Want to see more full solutions like this?
- Text Book Problem 7.82 (page 261) Consider the total head-loss in the system forthis flow is 18.56 ft (head-losses in first and second pipe are 13.83 ft and 4.73 ftrespectively). Please show numerical values for EGL/HGL at the beginning/end/intermediatechange point. (Point distribution: elevation determination 5 points, EGL, HGL lines 4points).(I think we are just using the values provided for head losses to solve this problem)arrow_forwardCalculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the moment distribution method, and draw the Shear force diagram and Bending moment diagram for the beam shown. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forwardCalculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the Slope deflection method. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forward
- Thank you for your help if you would also provide the equations used .arrow_forwardThe sectors are divided as follows:top right = 1, top left = 2, middle = 3, bottom = 4.(a) Determine the distance yˉ to the centroid of the beam’s cross-sectional area.Solve the next questions by building a table. (Table format Answers) (b) Determine the second moment of area (moment of inertia) about the x′ axis. (c) Determine the second moment of area (moment of inertia) about the y-axis.arrow_forwardinstructions: make sure to follow the instructions and provide complete and detailed solution create/draw a beam with uniformly distributed load and concentrated load after, find the shear and moment equation and ensure to draw it's shear and moment diagram once done, write it's conclusion or observation 4:57 PMarrow_forward
- Solve for forces on pin C and Darrow_forwardBorrow pit soil is being used to fill an 900,00 yd3 of depression. The properties of borrowpit and in-place fill soils obtained from laboratory test results are as follows:• Borrow pit soil: bulk density 105 pcf, moisture content = 8%, and specific gravity = 2.65• In-place fill soil: dry unit weight =120 pcf, and moisture content = 16%(a) How many yd3 of borrow soil is required?(b) What water mass is needed to achieve 16% moisture in the fill soil?(c) What is the in-place density after a long rain?arrow_forwardsolve for dt/dx=f(t,x)=x+t^2arrow_forward
- Calculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the slope deflection method, draw the resulting shear force diagran and bending moment diagram. The beam is subjected to an UDL of w=65m. L=4.5m, L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200 GPa, I = 250x106 mm4.arrow_forwardProblem 2 (A is fixed and C is a pin) Find the reactions and A and C. 10 k- 6 ft 6 ft B A 2 k/ft 15 ftarrow_forward6. A lake with no outlet is fed by a river with a constant flow of 1200 ft3/s. Water evaporates from the surface at a constant rate of 13 ft3/s per square mile of surface area. The surface area varies with the depth h (in feet) as A (square miles) = 4.5 + 5.5h. What is the equilibrium depth of the lake? Below what river discharge (volume flow rate) will the lake dry up?arrow_forward
