EBK MATHEMATICS FOR MACHINE TECHNOLOGY
8th Edition
ISBN: 9781337798396
Author: SMITH
Publisher: CENGAGE LEARNING - CONSIGNMENT
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 88, Problem 7AR
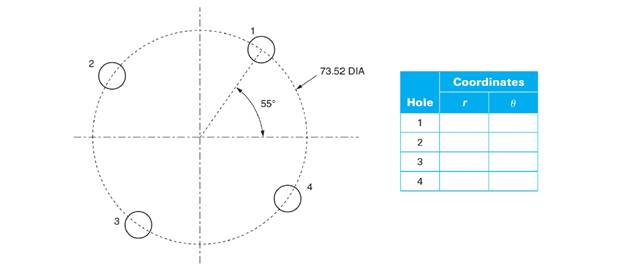
The following figure shows four equally spaced holes on a bolt circle circumference. Give the polar coordinates of each of the holes. All dimensions are in millimeters.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Suppose that a room containing 1300 cubic feet of air is originally free of carbon monoxide (CO). Beginning
at time t = 0, cigarette smoke containing 4% CO is introduced into the room at a rate of 0.8 cubic feet per
minute. The well-circulated smoke and air mixture is allowed to leave the room at the same rate.
Let A(t) represent the amount of CO in the room (in cubic feet) after t minutes.
(A) Write the DE model for the time rate of change of CO in the room. Also state the initial condition.
dA
dt
A(0)
(B) Solve the IVP to find the amount of CO in the room at any time t > 0.
A(t)
(C) Extended exposure to a CO concentration as low as 0.00012 is harmful to the human body. Find the time
at which this concentration is reached.
t=
minutes
Newton's Law of Cooling tells us that the rate of change of the temperature of an object is proportional to
the temperature difference between the object and its surroundings. This can be modeled by the
differential equation
dT
dt
k(TA), where T is the temperature of the object after t units of time
have passed, A is the ambient temperature of the object's surroundings, and k is a constant of
proportionality.
Suppose that a cup of coffee begins at 178 degrees and, after sitting in room temperature of 61 degrees
for 12 minutes, the coffee reaches 171 degrees. How long will it take before the coffee reaches 155
degrees?
Include at least 2 decimal places in your answer.
minutes
can you help me solve this question and show workings please
Chapter 88 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
Ch. 88 - Prob. 1ARCh. 88 - Refer to the points plotted on the Cartesian...Ch. 88 - Prob. 3ARCh. 88 - Prob. 4ARCh. 88 - Prob. 5ARCh. 88 - Prob. 6ARCh. 88 - The following figure shows four equally spaced...Ch. 88 - Prob. 8ARCh. 88 - Express the following decimal numbers as binary...Ch. 88 - Prob. 10AR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Let f : X → Y and g : Y → Z be two functions. Prove that(1) if g ◦ f is injective, then f is injective; (2) if g ◦ f is surjective, then g is surjective.arrow_forwardSolve the following boundary value problem using method of separation of variables ди 11.07 (137) 1 J²u + = = 0, -Пarrow_forwardNo chatgpt pls will upvotearrow_forwardEach answer must be justified and all your work should appear. You will be marked on the quality of your explanations. You can discuss the problems with classmates, but you should write your solutions sepa- rately (meaning that you cannot copy the same solution from a joint blackboard, for exam- ple). Your work should be submitted on Moodle, before February 7 at 5 pm. 1. True or false: (a) if E is a subspace of V, then dim(E) + dim(E) = dim(V) (b) Let {i, n} be a basis of the vector space V, where v₁,..., Un are all eigen- vectors for both the matrix A and the matrix B. Then, any eigenvector of A is an eigenvector of B. Justify. 2. Apply Gram-Schmidt orthogonalization to the system of vectors {(1,2,-2), (1, −1, 4), (2, 1, 1)}. 3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show…arrow_forward1. True or false: (a) if E is a subspace of V, then dim(E) + dim(E+) = dim(V) (b) Let {i, n} be a basis of the vector space V, where vi,..., are all eigen- vectors for both the matrix A and the matrix B. Then, any eigenvector of A is an eigenvector of B. Justify. 2. Apply Gram-Schmidt orthogonalization to the system of vectors {(1, 2, -2), (1, −1, 4), (2, 1, 1)}. 3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show that P - Q is its own inverse. 4. Show that the Frobenius product on n x n-matrices, (A, B) = = Tr(B*A), is an inner product, where B* denotes the Hermitian adjoint of B. 5. Show that if A and B are two n x n-matrices for which {1,..., n} is a basis of eigen- vectors (for both A and B), then AB = BA. Remark: It is also true that if AB = BA, then there exists a common…arrow_forwardQuestion 1. Let f: XY and g: Y Z be two functions. Prove that (1) if go f is injective, then f is injective; (2) if go f is surjective, then g is surjective. Question 2. Prove or disprove: (1) The set X = {k € Z} is countable. (2) The set X = {k EZ,nЄN} is countable. (3) The set X = R\Q = {x ER2 countable. Q} (the set of all irrational numbers) is (4) The set X = {p.√2pQ} is countable. (5) The interval X = [0,1] is countable. Question 3. Let X = {f|f: N→ N}, the set of all functions from N to N. Prove that X is uncountable. Extra practice (not to be submitted). Question. Prove the following by induction. (1) For any nЄN, 1+3+5++2n-1 n². (2) For any nЄ N, 1+2+3++ n = n(n+1). Question. Write explicitly a function f: Nx N N which is bijective.arrow_forward3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show that P - Q is its own inverse.arrow_forwardDetermine the moment about the origin O of the force F4i-3j+5k that acts at a Point A. Assume that the position vector of A is (a) r =2i+3j-4k, (b) r=-8i+6j-10k, (c) r=8i-6j+5karrow_forwardNot use ai pleasearrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Polar Coordinates Basic Introduction, Conversion to Rectangular, How to Plot Points, Negative R Valu; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=aSdaT62ndYE;License: Standard YouTube License, CC-BY