
The Environmental Protection Agency and the University of Florida recently cooperated in a large study of the possible effects of trace elements in drinking water on kidney-stone disease. The accompanying table presents data on age, amount of calcium in home drinking water (measured in parts per million), and smoking activity. These data were obtained from individuals with recurrent kidney-stone problems, all of whom lived in the Carolinas and the Rocky Mountain states.
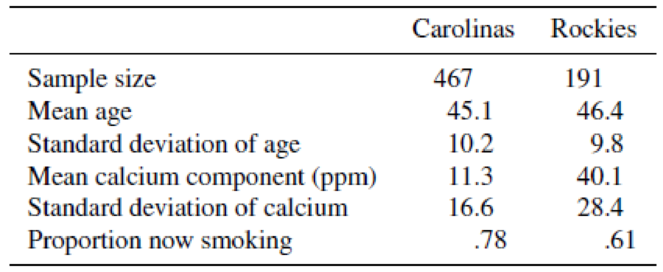
- a Estimate the average calcium concentration in drinking water for kidney-stone patients in the Carolinas. Place a bound on the error of estimation.
- b Estimate the difference in
mean ages for kidney-stone patients in the Carolinas and in the Rockies. Place a bound on the error of estimation. - c Estimate and place a 2-standard-deviation bound on the difference in proportions of kidney-stone patients from the Carolinas and Rockies who were smokers at the time of the study.
a.
Evaluate the mean calcium concentration in drinking water for kidney-stone patients in Region C.
Obtain the bound on error of estimation.
Answer to Problem 23E
The point estimate for the mean calcium concentration in drinking water for kidney-stone patients in Region C is 11.3 ppm.
The bound on the error of estimation is 1.5.
Explanation of Solution
Based on the given information, the data for calcium concentration in drinking water for kidney-stone patient in Region C is observed as given below:
The critical value has to be obtained for
Step-by-step procedure to obtain the critical value using Applet:
- Go to Applets/Simulations.
- Select Student’s t Probabilities and Quantiles.
- In df, enter 466.
- In Probability, enter 0.025.
The output obtained is as follows:
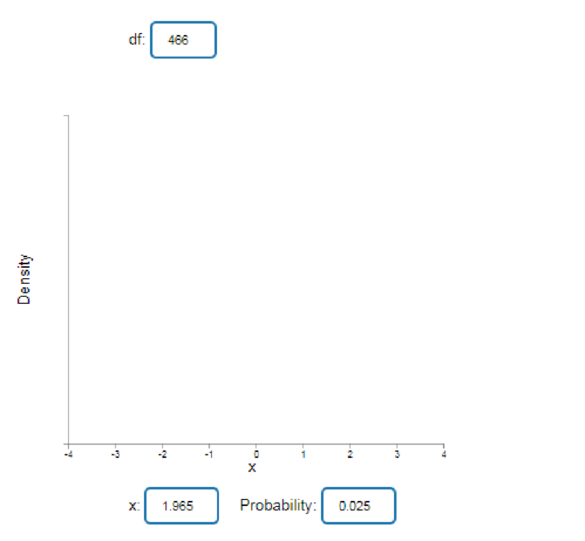
From the output, it is clear that the critical value is 1.965.
Substitute the values in two sided t-interval formula as given below:
Therefore, the point estimate for the mean calcium concentration in drinking water for kidney-stone patients in Region C is 11.3 ppm and the bound on the error of estimation is 1.5.
b.
Evaluate the difference in mean ages for kidney-stone patients in Region C and Region R.
Obtain the bound on error of estimation.
Answer to Problem 23E
The point estimate for the difference in mean ages for kidney-stone patients in Region C and Region R is −1.3
The bound on the error of estimation is 1.67.
Explanation of Solution
Based on the given information, the data are observed as given below:
Critical value:
The critical value is obtained as follows:
Step-by-step procedure to obtain the critical value using Applet:
- Go to Applets/Simulations.
- Select Student’s t Probabilities and Quantiles.
- In df, enter 656.
- In Probability, enter 0.025.
The output obtained is as follows:
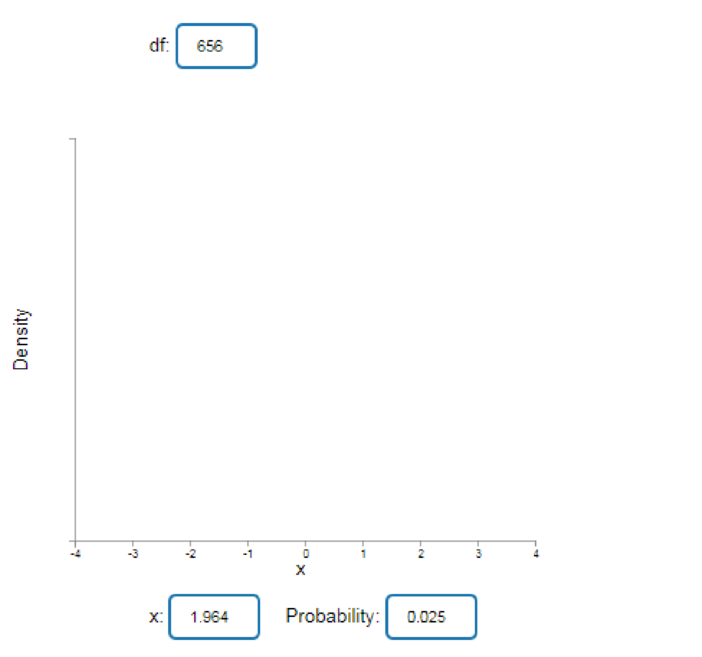
From the output, it is clear that the critical value is 1.964.
Substitute the values in two sided t-interval formula as given below:
Therefore, the point estimate for the difference in mean ages for kidney-stone patients in Region C and Region R is −1.3 and the bound on the error of estimation is 1.67.
c.
Evaluate and place 2-standard deviations bound on the difference in proportions of kidney-stone patients from Regions C and R.
Obtain the bound on error of estimation.
Answer to Problem 23E
The point estimate for the difference in proportions of kidney-stone patients from Regions C and R is 0.17, that is, (−2.97, 0.37).
The 2-standard deviations bound on the error of estimation is 0.0079.
Explanation of Solution
Based on the given information, the data are observed as given below:
The formula for difference in proportion is as follows:
Substitute the values as given below:
The point estimate for the difference in proportions of kidney-stone patients from Regions C and R is 0.17, and the 2-standard deviations bound on the error of estimation is 0.0079.
Want to see more full solutions like this?
Chapter 8 Solutions
Mathematical Statistics with Applications
- Question 2: When John started his first job, his first end-of-year salary was $82,500. In the following years, he received salary raises as shown in the following table. Fill the Table: Fill the following table showing his end-of-year salary for each year. I have already provided the end-of-year salaries for the first three years. Calculate the end-of-year salaries for the remaining years using Excel. (If you Excel answer for the top 3 cells is not the same as the one in the following table, your formula / approach is incorrect) (2 points) Geometric Mean of Salary Raises: Calculate the geometric mean of the salary raises using the percentage figures provided in the second column named “% Raise”. (The geometric mean for this calculation should be nearly identical to the arithmetic mean. If your answer deviates significantly from the mean, it's likely incorrect. 2 points) Starting salary % Raise Raise Salary after raise 75000 10% 7500 82500 82500 4% 3300…arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forward
- 310015 K Question 9, 5.2.28-T Part 1 of 4 HW Score: 85.96%, 49 of 57 points Points: 1 Save of 6 Based on a poll, among adults who regret getting tattoos, 28% say that they were too young when they got their tattoos. Assume that six adults who regret getting tattoos are randomly selected, and find the indicated probability. Complete parts (a) through (d) below. a. Find the probability that none of the selected adults say that they were too young to get tattoos. 0.0520 (Round to four decimal places as needed.) Clear all Final check Feb 7 12:47 US Oarrow_forwardhow could the bar graph have been organized differently to make it easier to compare opinion changes within political partiesarrow_forwardDraw a picture of a normal distribution with mean 70 and standard deviation 5.arrow_forward
- What do you guess are the standard deviations of the two distributions in the previous example problem?arrow_forwardPlease answer the questionsarrow_forward30. An individual who has automobile insurance from a certain company is randomly selected. Let Y be the num- ber of moving violations for which the individual was cited during the last 3 years. The pmf of Y isy | 1 2 4 8 16p(y) | .05 .10 .35 .40 .10 a.Compute E(Y).b. Suppose an individual with Y violations incurs a surcharge of $100Y^2. Calculate the expected amount of the surcharge.arrow_forward
- 24. An insurance company offers its policyholders a num- ber of different premium payment options. For a ran- domly selected policyholder, let X = the number of months between successive payments. The cdf of X is as follows: F(x)=0.00 : x < 10.30 : 1≤x<30.40 : 3≤ x < 40.45 : 4≤ x <60.60 : 6≤ x < 121.00 : 12≤ x a. What is the pmf of X?b. Using just the cdf, compute P(3≤ X ≤6) and P(4≤ X).arrow_forward59. At a certain gas station, 40% of the customers use regular gas (A1), 35% use plus gas (A2), and 25% use premium (A3). Of those customers using regular gas, only 30% fill their tanks (event B). Of those customers using plus, 60% fill their tanks, whereas of those using premium, 50% fill their tanks.a. What is the probability that the next customer will request plus gas and fill the tank (A2 B)?b. What is the probability that the next customer fills the tank?c. If the next customer fills the tank, what is the probability that regular gas is requested? Plus? Premium?arrow_forward38. Possible values of X, the number of components in a system submitted for repair that must be replaced, are 1, 2, 3, and 4 with corresponding probabilities .15, .35, .35, and .15, respectively. a. Calculate E(X) and then E(5 - X).b. Would the repair facility be better off charging a flat fee of $75 or else the amount $[150/(5 - X)]? [Note: It is not generally true that E(c/Y) = c/E(Y).]arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning



