Precalculus Enhanced with Graphing Utilities, Books a la Carte Edition Plus NEW MyLab Math -- Access Card Package (7th Edition)

7th Edition

ISBN: 9780134268231

Author: Michael Sullivan, Michael Sullivan III

Publisher: PEARSON

See similar textbooks

Concept explainers

Angles

In mathematics, angles constitute a very important part. Just like the concept of lines, an angle is a necessary figure that is used for measurement. How do you define its formation? It is formed when two or more lines meet at a point. The point at which…

Videos

Textbook Question

Chapter 8.3, Problem 53AE

Soccer Angles A soccer goal is 8 yards wide. Suppose a goalie is standing on her line in the center of her goal as a striker from the opposing team moves the ball towards her. The near post angle, $α$ , is formed by rays extending from the ball to the near post and the goalie. Similarly, the far post angle, $β$ , is formed by rays extending from the ball to the far post and the goalie. See the figure.

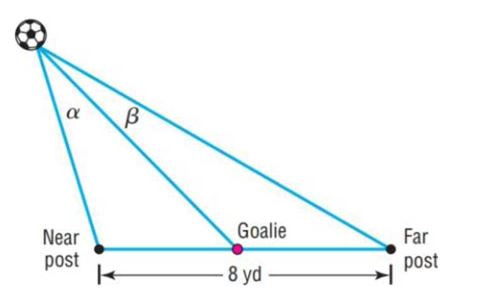
a. Determine the near post angle and the far post angle when the striker is 20 yards from the near post and 24 yards from the far post.

b. How far is the goalie from the ball?

c. To cover the near post, the goalie moves toward the near post in order to make the near post angle and the far post angle equal. How far toward her near post does the goalie need to move?

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 8.3, Problem 52AE

Chapter 8.3, Problem 54AE

Students have asked these similar questions

Ministry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Automobile Department Subject :Engineering Analysis Time: 2 hour Date:27-11-2022 کورس اول تحليلات تعمیر ) 1st month exam / 1st semester (2022-2023)/11/27 Note: Answer all questions,all questions have same degree. Q1/: Find the following for three only. 1- 4s C-1 (+2-3)2 (219) 3.0 (6+1)) (+3+5) (82+28-3),2- ,3- 2-1 4- Q2/:Determine the Laplace transform of the function t sint. Q3/: Find the Laplace transform of 1, 0≤t<2, -2t+1, 2≤t<3, f(t) = 3t, t-1, 3≤t 5, t≥ 5 Q4: Find the Fourier series corresponding to the function 0 -5

Ministry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Subject :Engineering Analysis Time: 80 min Date:11-12-2022 Automobile Department 2nd month exam / 1" semester (2022-2023) Note: Answer all questions,all questions have same degree. کورس اول شعر 3 Q1/: Use a Power series to solve the differential equation: y" - xy = 0 Q2/:Evaluate using Cauchy's residue theorem, sinnz²+cosz² dz, where C is z = 3 (z-1)(z-2) Q3/:Evaluate dz (z²+4)2 Where C is the circle /z-i/-2,using Cauchy's residue theorem. Examiner: Dr. Wisam N. Hassan

Chapter 8 Solutions

Precalculus Enhanced with Graphing Utilities, Books a la Carte Edition Plus NEW MyLab Math -- Access Card Package (7th Edition)

Ch. 8.1 - In a right triangle, if the length of the...Ch. 8.1 - If is an acute angle, solve the equation tan= 1 2...Ch. 8.1 - If is an acute angle, solve the equation sin= 1 2...Ch. 8.1 - True or False sin 52 =cos 48 Ch. 8.1 - The sum of the measures of the two acute angles in...Ch. 8.1 - When you look up at an object, the acute angle...Ch. 8.1 - True or False In a right triangle, if two sides...Ch. 8.1 - True or False In a right triangle, if we know the...Ch. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - In Problems 9-18, find the exact value of the six...

Additional Math Textbook Solutions

Find more solutions based on key concepts

For Problems 23-28, write in simpler form, as in Example 4. logbFG

Finite Mathematics for Business, Economics, Life Sciences and Social Sciences

Empirical versus Theoretical A Monopoly player claims that the probability of getting a 4 when rolling a six-si...

Introductory Statistics

First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...

Calculus: Early Transcendentals (2nd Edition)

Provide an example of a qualitative variable and an example of a quantitative variable.

Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561

The largest polynomial that divides evenly into a list of polynomials is called the _______.

Elementary & Intermediate Algebra

Find all solutions of each equation in the interval .

Precalculus: A Unit Circle Approach (3rd Edition)

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.