Chapter 8.2, Problem 35E

a.

To determine

To find: Whether it could be assumed that the condition required to construct a confidence interval for mean half-life is satisfied

Answer to Problem 35E

Yes

Explanation of Solution

Given:

The provided box plot is:

  

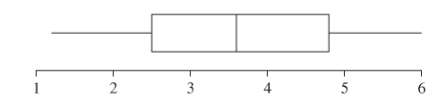
The provided box plot shows the mean half -life. In this no outlier is present, it could be said that this sample has been taken from the normally distributed population. Since, the normality condition is satisfied it could be assumed that the condition required to construct a confidence interval for mean half-life is satisfied

b.

To determine

To find: The confidence interval for the mean half-life the provided size range.

Answer to Problem 35E

The required confidence interval is $\left(2.93,4.23\right)$

Explanation of Solution

Formula used:

  $\overline{x}-t_{\frac{\alpha }{2},n-1}\times \frac{s}{\sqrt{n}}<\mu <\overline{x}+t_{\frac{\alpha }{2},n-1}\times \frac{s}{\sqrt{n}}$

Given:

Drug’s half-life of randomly selected 18 sample are:

3.3, 1.7, 2.0, 5.0, 1.2, 2.8, 3.7, 3.5, 4.8, 4.7, 4.9, 2.5, 5.1, 6.0, 3.9, 4.3, 2.1, 3.0

Calculation:

Since, sample size is less than 30 and population standard deviation is not known therefore, here t- distribution is to be used.

Sample mean and standard deviation for the provided sample data can be computed as:

  $\begin{array}{c}\overline{X}=\frac{{\displaystyle \sum _{i\in S}x}}{n}\\ =\frac{3.3+1.7+2+\mathrm{................}+3}{18}\\ =3.58\end{array}$

  $$

Data	Data-Mean	(Data-mean) ^2
3.3	-0.2	0.04
1.7	-1.88	3.5344
2	-1.58	2.4964
5	1.42	2.0164
1.2	-2.38	5.6644
2.8	-0.78	0.6084
3.7	0.12	0.0144
3.5	-0.08	0.0064
4.8	1.22	1.4884
4.7	1.12	1.2544
4.9	1.32	1.7424
2.5	-1.08	1.1664
5.1	1.52	2.3104
6	2.42	5.8564
3.9	0.32	0.1024
4.3	0.32	0.1024
2.1	1.32	1.7424
3	-0.58	0.3364

  $\begin{array}{c}s=\sqrt{\frac{{\displaystyle \sum _{i=1}^{12}{\left(x-\mu \right)}^2}}{n-1}}\\ =\sqrt{\frac{30.48}{18-1}}\\ =1.33\end{array}$

The 95% confidence interval for the mean prices can be calculated as:

  $\overline{x}\pm t_{\frac{\alpha }{2},n-1}\times \frac{s}{\sqrt{n}}$

Degree of freedom = 18-1 = 17.

Thus, t- critical (table) value at 5% significance level and 17 degree of freedom is

  $\begin{array}{c}CI=\overline{x}\pm t_{\frac{\alpha }{2},n-1}\times \frac{s}{\sqrt{n}}\\ =3.58\pm 2.10\times \frac{1.33}{\sqrt{18}}\\ =3.58\pm 0.65\\ =\left(2.93,4.23\right)\end{array}$

c.

To determine

To find: whether this confidence interval (part b) contradict the national health claims that the mean half-life 3.51

Answer to Problem 35E

Yes

Explanation of Solution

Since, the calculated confidence interval in part b ranges from 2.93 to 4.23, so it can be easily seen that the hypotheses value of national health includes in it