
Concept explainers
a)
Interpretation: Determine the order policy for the item based on silver-meal method.
Concept Introduction: Silver-Meal method is mainly used to determine the production quantities of the firm to be produced at the minimum cost.it is also provides the appropriate solutions to the time varying demand in production patterns.
a)
Answer to Problem 14P
The order policy according to silver meal method is 18 units in period-1,23 units in Period-4,50 units in Period-6,35 units in period-9 and 12 units in period-12.
Explanation of Solution
Given information: The anticipated demand for an inventory is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Demand | 6 | 12 | 4 | 8 | 15 | 25 | 20 | 5 | 10 | 20 | 5 | 12 |
Current inventory is 4 and ending inventory is 8.
Holding cost (h) is $1 per period, set up cost (K) is $40
The objective of this method is to minimize the per-period-cost of ordering policy.
Net Requirements:
The order policy (lot-size) of the item under silver meal method can be calculated as follows:
According to silver meal method the average cost per period C (T) is a function of the average holding and set up cost per period for T number of Periods. The production in period 1 is equal to the demand in that period 1 to incur the order cost K.
Hence
And
And general equation is
Once
Now, calculate the order policy using the above formula as follows:
Starting in period 1:
Stop the process since
Starting in period 4:
Stop the process since
Starting in period 6:
Stop the process since
Starting in period 9:
Stop the process since
The same is explained with the help of a table shown below:
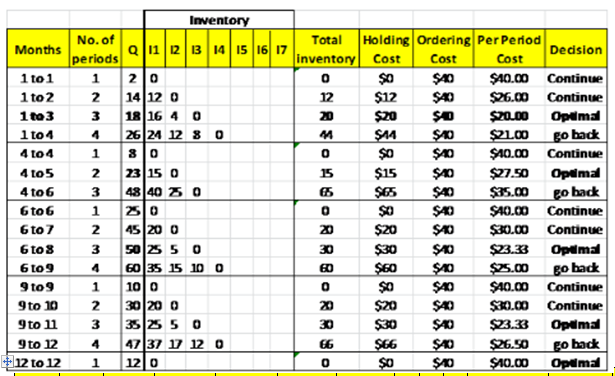
Table 1: Order Quantity using Silver-Meal Method:
| Months | No.of periods | Q | 11 | 12 | 13 | 14 | 15 | 16 | 17 | Total inventory | Holding Cost | Ordering Cost | Per Period Cost | Decision |
| 1 to 1 | 1 | 2 | 0 | =SUM(D3:J3) | =K3*1 | 40 | =SUM((L3:M3)/B3) | Continue | ||||||
| 1 to 2 | 2 | =2+12 | 12 | 0 | =SUM(D4:J4) | =K4*1 | 40 | =SUM((L4:M4)/B4) | Continue | |||||
| 1 to 3 | 3 | =14+4 | =C5-C3 | =C5-C4 | 0 | =SUM(D5:J5) | =K5*1 | 40 | =SUM((L5:M5)/B5) | Optimal | ||||
| 1 to 4 | 4 | =C5+8 | =C6-C3 | =C6-C4 | =C6-C5 | 0 | =SUM(D6:J6) | =K6*1 | 40 | =SUM((L6:M6)/B6) | Go Back | |||
| 4 to 4 | 1 | 8 | 0 | =SUM(D7:J7) | =K7*1 | 40 | =SUM((L7:M7)/B7) | Continue | ||||||
| 4 to 5 | 2 | =C7+15 | =C8-C7 | 0 | =SUM(D8:J8) | =K8*1 | 40 | =SUM((L8:M8)/B8) | Optimal | |||||
| 4 to 6 | 3 | =C8+25 | =C9-C7 | =C9-C8 | 0 | =SUM(D9:J9) | =K9*1 | 40 | =SUM((L9:M9)/B9) | Go Back | ||||
| 6 to 6 | 1 | 25 | 0 | =SUM(D10:J10) | =K10*1 | 40 | =SUM((L10:M10)/B10) | Continue | ||||||
| 6to 7 | 2 | =C10+20 | =C11-C10 | 0 | =SUM(D11:J11) | =K11*1 | 40 | =SUM((L11:M11)/B11) | Continue | |||||
| 6 to 8 | 3 | =C11+5 | =C12-C10 | =C12-C11 | 0 | =SUM(D12:J12) | =K12*1 | 40 | =SUM((L12:M12)/B12) | Optimal | ||||
| 6 to 9 | 4 | =C12+10 | =C13--C10 | =C13-C11 | =C13-C12 | =C13-C13 | =SUM(D13:J13) | =K13*1 | 40 | =SUM((L13:M13)/B13) | Go Back | |||
| 9 to 9 | 1 | 10 | 0 | =SUM(D14:J14) | =K14*1 | 40 | =SUM((L14:M14)/B14) | Continue | ||||||
| 9 to 10 | 2 | =C14+20 | =C15-C14 | 0 | =SUM(D15:J15) | =K15*1 | 40 | =SUM((L15:M15)/B15) | Continue | |||||
| 9 to 11 | 3 | =C15+5 | =C16-C14 | =C16-C15 | 0 | =SUM(D16:J16) | =K16*1 | 40 | =SUM((L16:M16)/B16) | Optimal | ||||
| 9 to 12 | 4 | =C16+12 | =C17--C14 | =C17-C15 | =C17-C16 | =C17-C17 | =SUM(D17:J17) | =K17*1 | 40 | =SUM((L17:M17)/B17) | Go Back | |||
| 12 to 12 | 1 | 12 | 0 | =SUM(D18:J18) | =K18*1 | 40 | =SUM((L18:M18)/B18) | Optimal |
b)
Interpretation: Determine the order policy for the item based on Least Unit Cost method.
Concept Introduction: Least unit cost produced the demand of the present periods based on the trial basis, yield the future periods. The method is calculated by adding the setup cost and carrying inventory cost and finally find the smallest cost per unit.
b)
Answer to Problem 14P
The order policy according to LUC method is 26 units in period-1, 40 units in Period-5, 25 units in Period-7, 35 units in period-9 and 12 units in period-12.
Explanation of Solution
Given information: The anticipated demand for a component VC is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Demand | 42 | 42 | 32 | 12 | 26 | 112 | 45 | 14 | 76 | 38 |
Holding cost (h) is $0.60 per period, set up cost (K) is $132
The order policy (lot-size) of the item under Least Unit Cost(LUC)method can be calculated as follows:
LUC divides the average cost per period C (T) by the total number of units demanded. Hence
And
And general equation is
Once
Starting from period 1
Stop the process since
Starting in period 5:
Stop the process since
Starting in period 7:
Stop the process since
Starting in period 9:
Stop the process since
The same is explained with the help of a table shown below:
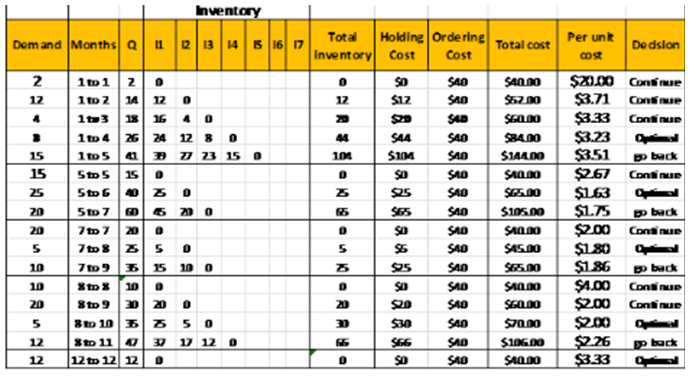
Table 2: Order Quantity using Least-Unit-Cost Method:
| Demand | Months | Q | 11 | 12 | 13 | 14 | 15 | Total inventory | Holding Cost | Ordering Cost | Total Cost | Per Period Cost | Decision |
| 2 | 1 to 1 | =A3 | 0 | =SUM(D3:H3) | =L3*1 | 40 | =K3+J3 | =L3/C3 | Continue | ||||
| 12 | 1 to 2 | =C3+A4 | =C4-C3 | 0 | =SUM(D4:H4) | =L4*1 | 40 | =K4+J4 | =L4/C4 | Continue | |||
| 4 | 1 to 3 | =C4+A5 | =C5-C3 | =C5-C4 | 0 | =SUM(D5:H5) | =L5*1 | 40 | =K5+J5 | =L5/C5 | Continue | ||
| 8 | 1 to 4 | =C5+A6 | =C6-C3 | =C6-C4 | =C6-C5 | =C6-C6 | =SUM(D6:H6) | =L6*1 | 40 | =K6+J6 | =L6/C6 | Optimal | |
| 15 | 1 to 5 | =C6+A7 | =C7-C3 | =C7-C4 | =C7-C5 | =C7-C6 | =C7-C7 | =SUM(D7:H7) | =L7*1 | =K7+J7 | =L7/C7 | Go Back | |
| 15 | 5 to 5 | =A8 | 0 | =SUM(D8:H8) | =L8*1 | 40 | =K8+J8 | =L8/C8 | Continue | ||||
| 25 | 5 to 6 | =C8+A9 | =C9-C8 | 0 | =SUM(D9:H9) | =L9*1 | 40 | =K9+J8 | =L9/C9 | Optimal | |||
| 20 | 5 to 7 | =C9+A11 | =C10-C8 | =C10-C9 | =C10-C10 | =SUM(D10:H10) | =L10*1 | 40 | =K10+J10 | =L10/C10 | Go Back | ||
| 20 | 7 to 7 | =A11 | 0 | =SUM(D11:H11) | =L11*1 | 40 | =K11+J11 | =L11/C11 | Continue | ||||
| 5 | 7 to 8 | =C11+A12 | =C12-C11 | 0 | =SUM(D12:H12) | =L12*1 | 40 | =K12+J12 | =L12/C12 | Optimal | |||
| 10 | 7 to 9 | =C12+A13 | =C13-C11 | =C13-C12 | =C13-C13 | =SUM(D13:H13) | =L13*1 | 40 | =K13+J13 | =L13/C13 | Go Back | ||
| 10 | 8 to 8 | =A14 | 0 | =SUM(D14:H14) | =L14*1 | 40 | =K14+J14 | =L14/C14 | Continue | ||||
| 20 | 8 to 9 | =C14+A15 | =C15-C14 | 0 | =SUM(D15:H15) | =L15*1 | 40 | =K15+J15 | =L15/C15 | Continue | |||
| 5 | 8 to 10 | =C15+A16 | =C16-C14 | =C16-C15 | 0 | =SUM(D16:H16) | =L16*1 | 40 | =K16+J16 | =L16/C16 | Optimal | ||
| 12 | 8 to 11 | =C16+A17 | =C17-C14 | =C17-C15 | -C17-C16 | =C17-C17 | =SUM(D17:H17) | =L17*1 | 40 | =K17+J17 | =L17/C17 | Go Back | |
| 12 | 12 to 12 | 12 | 0 | =SUM(D18:H18) | =L18*1 | 40 | =K18+J18 | ==L18/C18 | Optimal |
c)
Interpretation: Determine the order policy for the item based on Part Period Balancing method.
Concept Introduction: Part Period Balancing method is the lot-size method which use the starting and ending of the process function to consider the multiple periods to modifying the calculation based on the least total cost.
c)
Answer to Problem 14P
The order policy according to part period balancing method is 26 units in period-1, 60 units in Period-5, 35 units in Period-8, 17 units in period-11.
Explanation of Solution
Given information: The anticipated demand for a component VC is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Demand | 42 | 42 | 32 | 12 | 26 | 112 | 45 | 14 | 76 | 38 |
Holding cost (h) is $0.60 per period, set up cost (K) is $132
The order policy (lot size) according to part period balancing method can be calculated as follows:
In this method the order horizon that equates holding and setup cost over that period has to be calculated as follows:
Starting from Period 1
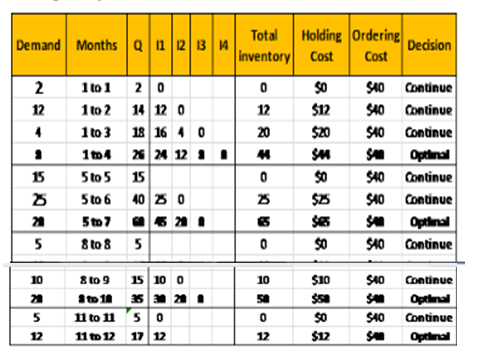
d)
Interpretation: Determine the three lot-sizing method resulted in the lowest cost for the 12 periods.
Concept Introduction: Lot size is determined the quantity order during the production time. The size of the lot may be dynamic or fixed.ERP (Enterprise Resource Planning) is the inbuilt multiple heuristic methods to determine the size of the lot to the production unit.
d)
Answer to Problem 14P
The Silver-meal method is giving lowest cost.
Explanation of Solution
Given information: The anticipated demand for a component VC is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Demand | 42 | 42 | 32 | 12 | 26 | 112 | 45 | 14 | 76 | 38 |
Holding cost (h) is $0.60 per period, set up cost (K) is $132
Calculate the total cost of the ordering for the three methods as shown below:
| Silver-meal | Least Unit Cost | Part Period Balancing | |
| Holding Cost | =20+15+30+30 | =44+25+5+30 | =44+65+50+12 |
| Setup Cost | =40*5 | =40*5 | =4*40 |
| Total Cost | =B3+B2 | =C3+C2 | =D3+D2 |
| Silver-meal | Least Unit Cost | Part Period Balancing | |
| Holding Cost | 95 | 104 | 171 |
| Setup Cost | 200 | 200 | 160 |
| Total Cost | 295 | 304 | 331 |
Want to see more full solutions like this?
Chapter 8 Solutions
EBK PRODUCTION AND OPERATIONS ANALYSIS
- Agree or disagree with the post When you get an insulting offer, the best thing to do is stay calm and professional. Try not to take it personally or react out of anger. Instead, ask questions to understand why the offer was so low. This helps you get a better idea of what the other person is thinking. After that, you can respond with a counteroffer that shows your value. Use simple facts like your skills, experience, and what others in your field are getting paid to back up your request. If the person still refuses to offer something fair, it’s okay to politely say no and walk away. Standing up for yourself in a respectful way shows confidence and helps others take you seriously. Agree or disagree with the postarrow_forwardRegarding perceptions that can occur when negotiating in different places and at different times, the continuation norm in e-negotiations is best described as _____. Group of answer choices A. negotiators' beliefs that negotiations are worth continuing B. the act of thinking about how things might have turned out differently C. the tendency for e-communicators to ascribe diabolical intentions to the other party D. the tendency for negotiators to behave as if they are communicating synchronously when in fact they are notarrow_forwardIn any discussion or meeting, there is a tendency for a minority of people to do most of the talking. A key determinant of who dominates the conversation is _____. Group of answer choices A. their status within the group B. their network of social connections C. their gender D. their agearrow_forward
- With regard to intergenerational negotiation, the _____ generation has vast numbers of relationships but few of them are deep. They spend more time communicating virtually than face-to-face. Their personal and work networks are vital to their on-the-fly learning and problem-solving skills. Armed with tools for working anywhere at any time, this generation puts more value in leading a balanced life and flexibility with their work and life demands. Group of answer choices A. mature B. boomer C. millennial D. Generation Xarrow_forwardIf a negotiator has less power than the counterparty and an unattractive BATNA, which communication medium might help the less-powerful negotiator claim more resources?arrow_forwardCould you help explain what the foundations of faith are? What are their strategies?arrow_forward
- Hi! Can you guys help me with this? Thank you! Please write-up summarizing the core message of the movie/documentary and the connection to the course material The documentary is Poisoned: The Dirty Truth About Your Food directed by Stephanie Soechtig from Netflix. * Here are the course material: Global Logistics Global Transportation; Global Inventory Management Global Operation Global Market Channels Purchasing Stategies: Outsourcing; Offshoring; Nearshoring; Multi-sourcing & Co-sourcing Make or Buy decisions Global Supply Chain Infrastructure: Transportation Infrastructure; Communication Infrastructure; Utilities Infrastructure; Technology Infrastructure Supply Chain Risks: • Supply Risks – disruption of supply, inventory and schedules. • Operational Risks – breakdown of operations, changes in technologies. • Demand Risks – variations in demand.• Security Risks – theft, sabotage, terrorism, counterfeiting.• Macro Risks – economic shifts, recession, wage hikes, varying…arrow_forwardHi! Can you guys help me with this? Thank you! Please write-up summarizing the core message of the movie/documentary and the connection to the course material The documentary is American Factory by Steven Bognar & Julia Reichert from Netflix * Here the course material: Global Logistics Global Transportation; Global Inventory Management Global Operation Global Market Channels Purchasing Stategies: Outsourcing; Offshoring; Nearshoring; Multi-sourcing & Co-sourcing Make or Buy decsions Global Supply Chain Infrastructure: Transportation Infrastructure; Communication Infrastructure; Utilities Infrastructure; Technology Infrastructure Supply Chain Risks: • Supply Risks – disruption of supply, inventory and schedules. • Operational Risks – breakdown of operations, changes in technologies. • Demand Risks – variations in demand.• Security Risks – theft, sabotage, terrorism, counterfeiting.• Macro Risks – economic shifts, recession, wage hikes, varying exchangerates.• Policy Risks –…arrow_forward1) View the video Alton Bridge (12.16 mins, Ctrl + Click on the link), and please answer the following questions: https://meida.gaspar.mheducation.com/GASPARPlayer/play.html?id=24qHEm8aNZExFciJtZQbqli a) According to the video, what are the various steps involved in managing projects? b) What were the different phases of the Alton Bridge project? c) What are the two widely used scheduling techniques, and under what phase of the Alton Bridge project are they discussed? Note: As a rough guideline, please try to keep the written submission to a paragraph or so for each of the questions. 2) The following is a table of activities associated with a mining project at Lunar Industries, their durations, and what activities each must precede: Activity Duration (weeks) Precedes A (start) 1 B, C B 1 E C 4 F E 2 F F (end) 2 - The AOM project diagram is as given below: a) What is the critical path (list all activities in the…arrow_forward
- 1) View the video Alton Bridge (12.16 mins, Ctrl + Click on the link), and please answer the following questions: a) According to the video, what are the various steps involved in managing projects? b) What were the different phases of the Alton Bridge project? c) What are the two widely used scheduling techniques, and under what phase of the Alton Bridge project are they discussed? Note: As a rough guideline, please try to keep the written submission to a paragraph or so for each of the questions. 2) The following is a table of activities associated with a mining project at Lunar Industries, their durations, and what activities each must precede: Activity Duration (weeks) Precedes A (start) 1 B, C B 1 E C 4 F E 2 F F (end) 2 - The AOM project diagram is as given below:arrow_forwardWith all the problems companies are currently facing, why do so many choose to expand into international markets? What are the advantages of expanding beyond the domestic market?arrow_forwardPerform resource leveling. Assume that each task can be performed independently of the other tasks.arrow_forward
 Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning
Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,- MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing



