Chapter 8, Problem 8.8P

Interpretation Introduction

Interpretation:

The thermal efficiency of the cycle and the fraction of the steam entering the turbine is extracted for the feed water heater should be determined.

Concept Introduction:

The thermal efficiency of the cycle is calculated as:

  $\eta =\frac{\left|W_{net}\right|}{Q_H}$

Here $W_{net}$ is the total work produced by the turbine and pump. $Q_H$ is the difference in enthalpies of the turbine and boiler.

The entropy is constant for idealistic turbine. Hence an isentropic process is developed between the enter and exit pressures of the idealistic turbine. The idealistic condenser has constant enthalpy.

Answer to Problem 8.8P

  $\eta =0.311$

And

  $m=0.1868{\text{lb}}_m$

Explanation of Solution

Given information:

It is given thatcycle is a regenerative cycle in a steam power plant includes one feedwater heater, turbine, condenser and a boiler. Steam enters the turbine at $650{\text{psia and 900}}^{\circ }\text{F}$ and exhaust at $1\text{psia}$ to condenser and $50\text{psia}$ to feedwater heater. Steam for the feedwater heater is at $50\text{psia}$ and in condensing raises the temperature of the feedwater to within ${11}^{\circ }\text{F}$ . Turbine and pump efficiencies are both given as $0.78$ .

Figure to describe the process in simplified form is given as below

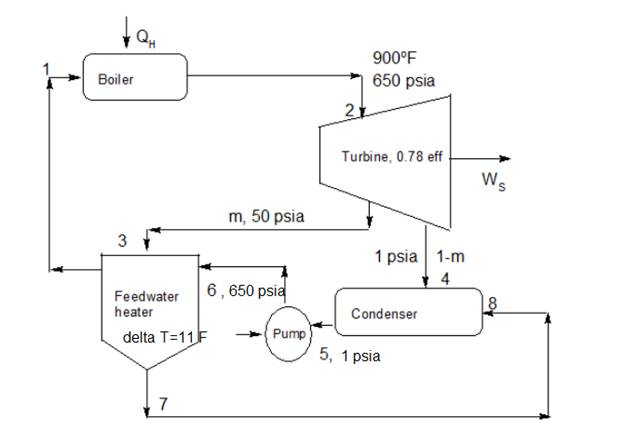
From figure point 1 and point 6 has same operating conditions.

Considering idealistic turbine for which entropy is constant at inlet and outlet

at point 2 and at $650{\text{psia and 900}}^{\circ }\text{F}$, the properties are written from superheated steam table in fps unit as,

  $H_2=1461.2\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}$ and $S_2=1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$

Now for idealistic turbine, entropy is constant at inlet and outlet. Hence

  $S_4{}^{\text{'}}=S_3{}^{\text{'}}=S_2=1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$

Exhaust coming to condenser is at pressure $1\text{psia}$ and entropy $S_4{}^{\text{'}}=1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$ and turbine has thermal efficiency of $0.78$ . Hence, we need to calculate the actual entropy of the steam coming to condenser inlet at point 4.

The steam coming to condenser is wet and saturated. Hence for saturated steam at $1\text{psia}$, properties are written from the steam table for the saturated steam at $1\text{psia}$ as,

At $0.94924\text{psia}$

  $\begin{array}{l}{H}_{\text{liq}}=67.999\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\text{and}{H}_{\text{vap}}=1105.1\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\\ S_{\text{liq}}=0.1295\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\text{and}{S}_{\text{vap}}=1.9825\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\end{array}$

At $1.00789\text{psia}$

  $\begin{array}{l}{H}_{\text{liq}}=69.995\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\text{and}{H}_{\text{vap}}=1105.9\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\\ S_{\text{liq}}=0.1331\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\text{and}{S}_{\text{vap}}=1.9775\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\end{array}$

From linear interpolation, if $M$ is the function of a single independent variable $X$ then the value of $M$ at $X$ is intermediate between two given values, $M_1$ at $X_1$ and $M_2$ at $X_2$

  $\begin{array}{l}M=\left(\frac{X_2-X}{X_2-X_1}\right)M_1+\left(\frac{X-X_1}{X_2-X_1}\right)M_2\\ \\ H_{\text{liq}}=\left(\frac{1.00789\text{psia}-1\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 67.999\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}+\left(\frac{1\text{psia}-0.94924\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 69.995\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\\ \\ H_{\text{liq}}=69.73\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\end{array}$

Similarly

  $\begin{array}{l}M=\left(\frac{X_2-X}{X_2-X_1}\right)M_1+\left(\frac{X-X_1}{X_2-X_1}\right)M_2\\ \\ H_{\text{Vap}}=\left(\frac{1.00789\text{psia}-1\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 1105.1\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}+\left(\frac{1\text{psia}-0.94924\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 1105.9\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\\ \\ H_{\text{vap}}=1105.79\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\end{array}$

And

  $\begin{array}{l}M=\left(\frac{X_2-X}{X_2-X_1}\right)M_1+\left(\frac{X-X_1}{X_2-X_1}\right)M_2\\ \\ S_{\text{Vap}}=\left(\frac{1.00789\text{psia}-1\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 1.9825\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}+\left(\frac{1\text{psia}-0.94924\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 1.9775\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\\ \\ S_{\text{vap}}=1.9781\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\end{array}$

  $\begin{array}{l}M=\left(\frac{X_2-X}{X_2-X_1}\right)M_1+\left(\frac{X-X_1}{X_2-X_1}\right)M_2\\ \\ S_{liq}=\left(\frac{1.00789\text{psia}-1\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 0.1295\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}+\left(\frac{1\text{psia}-0.94924\text{psia}}{1.00789\text{psia-}0.94924\text{psia}}\right)\times 0.1331\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\\ \\ S_{liq}=0.1326\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\end{array}$

And

We also know that

  $\begin{array}{l}{S}_4{}^{\text{'}}=S_{liq}+x_4{}^{\text{'}}\left(S_{vap}-S_{liq}\right)\\ \\ \Rightarrow x_4{}^{\text{'}}=\frac{S_4{}^{\text{'}}-S_{liq}}{S_{vap}-S_{liq}}\\ \\ \Rightarrow x_4{}^{\text{'}}=\frac{1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}-0.1326\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}}{1.9781\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}-0.1326\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}}\\ \\ \Rightarrow x_4{}^{\text{'}}=0.831\end{array}$

Therefore,

  $\begin{array}{l}{H}_4{}^{\text{'}}=H_{liq}+x_4{}^{\text{'}}\left(H_{vap}-H_{liq}\right)\\ \\ H_4{}^{\text{'}}=69.73\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}+0.831\times \left(1105.79\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-69.73\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\right)\\ \\ H_4{}^{\text{'}}=931.195\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\end{array}$

Hence the actual enthalpy of the steam exhaust from the turbine to the condenser is calculated by the thermodynamics efficiency of the work produced from the turbine which is

  $\begin{array}{l}\eta =\frac{W_{actual}}{W_{ideal}}\\ \Rightarrow \eta =\frac{H_4-H_2}{H_4{}^{\text{'}}-H_2}\\ \Rightarrow 0.78=\frac{H_4-1461.2\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}}{931.195\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-1461.2\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}}\\ \\ \Rightarrow H_4=1047.796\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\end{array}$

Hence

  $\begin{array}{l}{H}_4=H_{liq}+x_4\left(H_{vap}-H_{liq}\right)\\ \\ \Rightarrow x_4=\frac{H_4-H_{liq}}{H_{vap}-H_{liq}}\\ \\ \Rightarrow x_4=\frac{1047.796\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-69.73\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}}{1105.79\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-69.73\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}}\\ \\ \Rightarrow x_4=0.944\end{array}$

and

  $\begin{array}{l}{S}_4=S_{liq}+x_4\left(S_{vap}-S_{liq}\right)\\ \\ S_4=0.1326\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}+0.944\times \left(1.9781\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}-0.1326\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\right)\\ \\ S_4=1.8748\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\end{array}$

Exhaust coming to feedwater heater is at pressure $50\text{psia}$ and entropy $S_3{}^{\text{'}}=1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$ and turbine has thermal efficiency of $0.78$ . Hence, we need to calculate the actual entropy of the steam coming to feedwater heater inlet at point 3.

The steam coming to feedwater heater is superheated. Hence for superheated steam at $50\text{psia}$, properties are written from the steam table for the superheated steam at $50\text{psia}$ as,

  $50\text{psia}$ and $S_3{}^{\text{'}}=1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$ lies in between $50\text{psia}$ and $S_3{}^{\text{'}}=1.6586\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$ with enthalpy $1174.1\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}$ and $50\text{psia}$ and $S_3{}^{\text{'}}=1.6720\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$ with enthalpy $1184.1\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}$

From linear interpolation, if $M$ is the function of a single independent variable $X$ then the value of $M$ at $X$ is intermediate between two given values, $M_1$ at $X_1$ and $M_2$ at $X_2$

  $\begin{array}{l}M=\left(\frac{X_2-X}{X_2-X_1}\right)M_1+\left(\frac{X-X_1}{X_2-X_1}\right)M_2\\ \\ H_3{}^{\text{'}}=\left(\frac{1.6720\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}-1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}}{1.6720\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\text{-}1.6586\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}}\right)\times 1174.1\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}+\\ \left(\frac{1.6671\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}-1.6586\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}}{1.6720\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\text{-}1.6586\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}}\right)\times 1184.1\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\\ \\ H_3{}^{\text{'}}=1180.44\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\end{array}$

Hence the actual enthalpy of the steam exhaust from the turbine to the feedwater heater is calculated by the thermodynamics efficiency of the work produced from the turbine which is

  $\begin{array}{l}\eta =\frac{W_{actual}}{W_{ideal}}\\ \Rightarrow \eta =\frac{H_3-H_2}{H_3{}^{\text{'}}-H_2}\\ \Rightarrow 0.78=\frac{H_3-1461.2\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}}{1180.44\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-1461.2\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}}\\ \\ \Rightarrow H_3=1242.21\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\end{array}$

And entropy at $H_3=1242.21\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}$ and $50\text{psia}$ from superheated steam table in fps unit after the interpolation is

  $S_3=1.7431\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}$

Now,

The idealistic condenser has constant enthalpy and hence the enthalpy of saturated liquid at inlet point 4 of condenser is same as enthalpy at the outlet of condenser at point 5.

  $H_5=H_{\text{liq}}=69.73\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}$

And at $1\text{psia}$, the volume of saturated liquid at outlet of condenser point 5 is written from the saturated steam table in fps units after the interpolation as

  $V_5=0.0161\frac{{\text{ft}}^3}{{\text{lb}}_{\text{m}}}$

Hence work required for circulation of the steam from the condenser to the feedwater heater is calculated fromusing the pump efficiency is

  $\begin{array}{l}\eta =\frac{W_{ideal}}{W_{actual}}\\ \\ W_{actual}=W_{pump}=\frac{W_{ideal}}{\eta }\\ \\ \Rightarrow W_{pump}=\frac{V_5\left(P_6-P_5\right)}{\eta }\\ \\ \Rightarrow W_{pump}=\frac{0.0161\frac{{\text{ft}}^3}{{\text{lb}}_{\text{m}}}\left(650\frac{{\text{lb}}_f}{{\text{in}}^2}-1\frac{{\text{lb}}_f}{{\text{in}}^2}\right)\times \frac{{12}^2{\text{in}}^2}{1{\text{ft}}^2}}{0.78}\\ \\ \Rightarrow W_{pump}=1920.11\frac{{\text{lb}}_f.\text{ft}}{{\text{lb}}_m}\times \frac{1\text{Btu}}{778.17{\text{lb}}_f.\text{f}}=2.47\frac{\text{Btu}}{{\text{lb}}_m}\end{array}$

And the work-done by pump is also calculated as

  $\begin{array}{l}\Rightarrow W_{pump}=H_6-H_5=2.47\frac{\text{Btu}}{{\text{lb}}_m}\\ \\ \Rightarrow H_6=2.47\frac{\text{Btu}}{{\text{lb}}_m}+69.73\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\\ \\ \Rightarrow H_6=72.197\frac{\text{Btu}}{{\text{lb}}_m}\end{array}$

Now it is given that steam for the feedwater heater is at $50\text{psia}$ and in condensing raises the temperature of the feedwater to within ${11}^{\circ }\text{F}$ .

Hence at point 7 the steam is saturated liquid from feedwater heater going towards the condenser. Hence for $50\text{psia}$ and saturated steam, for saturated steam table, properties are written as,

  $\begin{array}{l}{H}_{\text{liq}}=H_7=250.21\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\text{and}{S}_{\text{liq}}=S_7=0.4112\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\\ T_7={281.01}^{\circ }\text{F}\end{array}$

Hence the temperature at the point 1 according to the given condition and in condensing raises the temperature of the feedwater to within ${11}^{\circ }\text{F}$ is

  $\begin{array}{l}{T}_1={281.01}^{\circ }{\text{F-11}}^{\circ }\text{F}\\ T_1={270.01}^{\circ }\text{F}\end{array}$

And at $T_1={270.01}^{\circ }\text{F}$, for saturated liquid from feedwater heater going towards the boiler, the properties are written from saturated steam table after interpolation as,

  $\begin{array}{l}{H}_{\text{liq}}=238.96\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\text{and}{S}_{\text{liq}}=0.3960\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\\ P^{sat}=41.87\text{psia,}{V}_{liq}=0.1717\frac{{\text{ft}}^3}{{\text{lb}}_m}\end{array}$

The volume expansivity for boiler is calculated as

  $\begin{array}{l}\beta =\frac{1}{V}\left(\frac{\partial V}{\partial T}\right)=\frac{1}{0.1717\frac{{\text{ft}}^3}{{\text{lb}}_m}}\times \left(\frac{0.01738\frac{{\text{ft}}^3}{{\text{lb}}_m}-0.017193\frac{{\text{ft}}^3}{{\text{lb}}_m}}{{292}^{\circ }\text{F}-{\text{272}}^{\circ }\text{F}}\right)\\ \\ \Rightarrow \beta =5.445\times {10}^{-5}\frac{1}{\text{Rankine}}\end{array}$

Hence the enthalpy and entropy across the boiler is

  $\begin{array}{l}\Delta H=V\left(1-\beta T\right)\Delta P\\ \Rightarrow H_1-H_{liq}=V_{liq}\left(1-\beta T_1\right)\left(P_1-P^{sat}\right)\\ \\ H_1-238.96\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}=0.1717\frac{{\text{ft}}^3}{{\text{lb}}_m}\times \left(1-\left(5.445\times {10}^{-5}\frac{1}{\text{Rankine}}\times \left({270.01}^{\circ }\text{F+459}\text{.67}\right)\text{Rankine}\right)\right)\\ \times \left(650\text{Psia}-41.87\text{psia}\right)\times \frac{{12}^2{\text{in}}^2}{1{\text{ft}}^2}\times \frac{1\text{Btu}}{778.17{\text{lb}}_f.\text{f}}\\ H_1=257.51\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\end{array}$

And

  $\begin{array}{l}\Delta S=\beta V\Delta P\\ \Rightarrow S_1-S_{liq}=\beta V_{liq}\left(P_1-P^{sat}\right)\\ \\ S_1-0.3960\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}=0.1717\frac{{\text{ft}}^3}{{\text{lb}}_m}\times 5.445\times {10}^{-5}\frac{1}{\text{Rankine}}\times \left(650\text{Psia}-41.87\text{psia}\right)\times \frac{{12}^2{\text{in}}^2}{1{\text{ft}}^2}\times \frac{1\text{Btu}}{778.17{\text{lb}}_f.\text{f}}\\ S_1=0.397\frac{\text{Btu}}{{\text{lb}}_{\text{m}}\text{Rankine}}\end{array}$

Let mass of steam exhaust from the turbine going towards feedwater heater is $m$ hence mass of steam exhaust from turbine going towards condenser is $\left(1-m\right)$

Basis $1{\text{lb}}_m\text{of steam exhaust of turbine}$

Applying energy balance across the feedwater heater. Hence fraction of the steam entering the turbine is extracted for the feedwater heater is

  $\begin{array}{l}m{H}_3+1{\text{lb}}_m{H}_6=\left(1-m\right)H_7+m{H}_1\\ \\ m{H}_3+1{\text{lb}}_m{H}_6=m{H}_7+1{\text{lb}}_m{H}_1\\ \\ m\left(H_3-H_7\right)=1{\text{lb}}_m\left(H_1-H_6\right)\\ \\ \Rightarrow m=\frac{H_1-H_6}{H_3-H_7}\\ \\ m=\frac{257.51\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-72.197\frac{\text{Btu}}{{\text{lb}}_m}}{1242.21\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-250.21\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}}\\ \\ m=0.1868{\text{lb}}_m\end{array}$

And

The thermal efficiency of the cycle is calculated as:

  $\eta =\frac{\left|W_{net}\right|}{Q_H}$

Here $W_{net}$ is the total work produced by the turbine and pump. $Q_H$ is the difference in enthalpies of the turbine and boiler.

  $\begin{array}{l}{W}_{\text{turbine-1st}}=\eta \left(H_3{}^{\text{'}}-H_2\right)=-218.99\frac{\text{Btu}}{{\text{lb}}_m}\times 1{\text{lb}}_m=-218.99\text{Btu}\\ \\ W_{\text{turbine-2nd}}=\left(1-m\right)\left(H_4-H_3\right)=\left(1{\text{lb}}_m-0.1868{\text{lb}}_m\right)\times \left(1047.796\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-1242.21\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\right)\\ W_{\text{turbine-2nd}}=-158.098\text{Btu}\\ \\ W_{pump}=2.47\frac{\text{Btu}}{{\text{lb}}_m}\times 1{\text{lb}}_m=2.47\text{Btu}\\ \\ \Rightarrow \eta =\frac{\left|W_{\text{turbine-1st}}+W_{\text{turbine-2nd}}+W_{pump}\right|}{\left(H_2-H_1\right)}\\ \\ \Rightarrow \eta =\frac{\left|\left(-218.99\text{Btu}\right)+\left(-158.098\text{Btu}\right)+2.47\text{Btu}\right|}{\left(1461.2\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}-257.51\frac{\text{Btu}}{{\text{lb}}_{\text{m}}}\right)}\\ \\ \Rightarrow \eta =0.311\end{array}$

Conclusion

  $\eta =0.311$

And

  $m=0.1868{\text{lb}}_m$