Chapter 8, Problem 8.6.4P

To determine

(a)

The design of a three-plate moment connection of a $W18\times 35$ beam to a $W14\times 99$ column for the given conditions by using LRFD.

Answer to Problem 8.6.4P

$PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$with 20 bolts.

Use a $PL\frac{1}{4}\times 3\frac{1}{2}\times 10\frac{1}{2}$with four 5/8-in. diameter Group A bolts for the web plate.

1/8-in. fillet weld on both sides of the plate.

Use a $PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$with twenty ½-in. diameter Group A bolts for each flange plate.

Explanation of Solution

Given:

Service dead-load moment = 42 ft-kips

Service live-load moment = 104 ft-kips

Service dead-load beam reaction = 8 kips

Service live-load beam reaction = 21 kips

Group A bearing type bolts

E70 electrodes

A992 steel- Beam and column

A36 steel- Plate material

Calculation:

Reaction:

$R_u=1.2D+1.6L=1.2\left(8\right)+1.6\left(21\right)=43.2kips$

Moment:

$M_u=1.2M_D+1.6M_L=1.2\left(42\right)+1.6\left(104\right)=216.8ft-kips$

Web plate:

Neglect eccentricity.

Try 5/8-in. diameter bolts.

Assume that threads are in the plane of shear.

$A_b=\frac{\pi d^2}{4}=\frac{\pi {\left(5/8\right)}^2}{4}=0.3068in{.}^2$

Shear capacity of one bolt is

$\varphi R_n=\varphi F_{nv}{A}_b=0.75\left(54\right)\left(0.3068\right)=12.43kips/bolt$

Number of bolts required is

$\frac{43.2}{12.43}=3.48$

Try 4 bolts.

Determine plate thickness required for bearing. Assume that

$\varphi R_n=\varphi \left(2.4dt{F}_u\right)=0.75\left(2.4\right)\left(5/8\right)t\left(58\right)=65.25t$

Load resisted by each bolt = $\frac{43.2}{4}=10.8kips$

Let $\varphi R_n=10.8=65.25t$

$t=0.166in.$

Try $t=\frac{3}{16}in.$

Determine whether plate or beam web controls bearing. For the plate,

$t{F}_u=\frac{3}{16}\left(58\right)=10.9kips/in.$

For the beam web, $t_w{F}_u=0.3\left(65\right)=19.5kips/in.>10.9kips/in.$

Therefore, plate controls.

Check bearing strength assumption:

$h=\frac{5}{8}+\frac{1}{16}=\frac{11}{16}in.$

For the hole nearest the edge, minimum $l_e=\frac{7}{8}in.$

Try $1\frac{1}{2}in.$

$\begin{array}{l}{l}_c=l_e-\frac{h}{2}=1.5-\frac{11/16}{2}=1.156in.\\ \varphi R_n=\varphi \left(1.2l_{c}t{F}_u\right)=0.75\left(1.2\right)\left(1.156\right)\left(3/16\right)58=11.31kips\\ \varphi \left(2.4dt{F}_u\right)=0.75\left(2.4\right)\left(5/8\right)\left(3/16\right)58=12.23kips>11.31kips\end{array}$

Therefore, use $\varphi R_n=11.31kips/bolt$

For other bolts, minimum $s=2.667\left(5/8\right)=1.667in.$

Use $s=2\frac{1}{2}in.$

$\begin{array}{l}{l}_c=s-h=2.5-\frac{11}{16}=1.813in.\\ \varphi R_n=\varphi \left(1.2l_{c}t{F}_u\right)=0.75\left(1.2\right)\left(1.813\right)\left(3/16\right)\left(58\right)=17.74kips\\ \varphi \left(2.4dt{F}_u\right)=12.23kips<17.74kips\end{array}$

Therefore, use $\varphi R_n=12.23kips/bolt$

Bearing controls over shear at each bolt location. Total strength is

$11.31+3\left(12.23\right)=48kips>43.2kips$ (OK)

Use four 5/8-in. diameter Group A bolts.

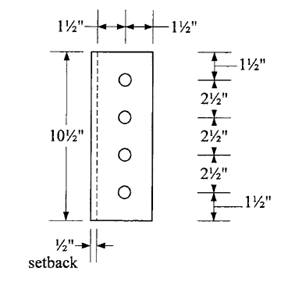
Determine plate thickness required for shear:

Shear yielding strength is

$\varphi R_n=1.0\left(0.6F_y{A}_{gv}\right)$

Let $43.2=1.0\left(0.6\right)\left(36\right)\left(10.5t\right)$

$t=0.191in.$

Try $t=\frac{1}{4}in.$

Check shear rupture strength:

Use hole diameter = $\frac{5}{8}+\frac{1}{8}=\frac{3}{4}in.$

$\begin{array}{l}{A}_{nv}=\left(10.5-4\times \frac{3}{4}\right)\frac{1}{4}=1.875in{.}^2\\ \varphi R_n=\varphi \left(0.6F_u{A}_{nv}\right)=0.75\left(0.6\right)\left(58\right)\left(1.875\right)\end{array}$

$=48.9kips>43.2kips$ (OK)

Check block shear:

Shear areas:

$\begin{array}{l}{A}_{gv}=\frac{1.5+3\times 2.5}{4}=2.25in{.}^2\\ A_{nv}=\frac{9-3.5\left(3/4\right)}{4}=1.594in{.}^2\end{array}$

Tension area:

$\begin{array}{l}{A}_{nt}=\frac{1.5-0.5\left(3/4\right)}{4}=0.2813in{.}^2\\ R_n=0.6F_u{A}_{nv}+U_{bs}{F}_u{A}_{nt}\\ =0.6\left(58\right)\left(1.594\right)+1.0\left(58\right)\left(0.2813\right)=71.79kips\end{array}$

with an upper limit of

$0.6F_y{A}_{gv}+U_{bs}{F}_u{A}_{nt}=0.6\left(36\right)\left(2.25\right)+1.0\left(58\right)\left(0.2813\right)=64.92kips$

The nominal block shear strength is therefore 64.92 kips. The design block shear strength is

$\varphi R_n=0.75\left(64.92\right)=48.7kips>43.2kips$ (OK)

Use a $PL\frac{1}{4}\times 3\frac{1}{2}\times 10\frac{1}{2}$ as shown above.

Connection of shear plate to column flange:

Use E70 electrodes

Minimum weld size, based on the plate thickness, is 1/8-in. try $w=\frac{1}{8}in.$

Weld strength = $1.392\times 2=2.784kips/in.$

Base metal (plate) shear strength:

Yielding:

$\varphi R_n=1.0\left(0.6F_{y}t\right)=1.0\left(0.6\right)\left(36\right)\left(1/4\right)=5.4kips/in.>2.784kips/in.$

Rupture:

$\varphi R_n=0.75\left(0.6F_{u}t\right)=0.45F_{u}t=0.45\left(58\right)\left(1/4\right)=6.525kips/in.>2.784kips/in.$

Total length required = $\frac{43.2}{2.784}=15.5in.$

Use a continuous 1/8-in. fillet weld, both sides of plate.

Flange plate:

From $M=Hd$,

$H=\frac{M}{d}=\frac{216.8\left(12\right)}{17.7}=147kips$

Try 7/8-in. diameter bolts.

Assume that threads are in the plane of shear.

$\begin{array}{l}{A}_b=\frac{\pi {\left(7/8\right)}^2}{4}=0.6013in{.}^2\\ \varphi R_n=0.75\left(54\right)\left(0.6013\right)=24.35kips/bolt\end{array}$

Number of bolts required for shear is

$\frac{147}{24.35}=6.04$

Try 8 bolts (4 pair)

Determine plate thickness required for bearing:

$h=\frac{7}{8}+\frac{1}{16}=\frac{15}{16}in.$

Minimum $l_e=1\frac{1}{2}in.$

Use $1\frac{1}{2}in.$

Minimum $s=2.667\left(\frac{7}{8}\right)=2.33in.$

Use $2\frac{1}{2}in.$

For the hole nearest the edge,

$l_c=l_e-\frac{h}{2}=1.5-\frac{15/16}{2}=1.031in.$

$\begin{array}{l}\varphi R_n=\varphi \left(1.2l_{c}t{F}_u\right)=0.75\left(1.2\right)\left(1.031\right)t\left(58\right)=53.82tkips\\ \varphi \left(2.4dt{F}_u\right)=0.75\left(2.4\right)\left(\frac{7}{8}\right)t\left(58\right)=91.35tkips>53.82tkips\end{array}$

Therefore, use $\varphi R_n=53.82tkips/bolt$

For other bolts,

$\begin{array}{l}{l}_c=s-h=2.5-\frac{15}{16}=1.563in.\\ \varphi R_n=\varphi \left(1.2l_{c}t{F}_u\right)=0.75\left(1.2\right)\left(1.563\right)t\left(58\right)=81.59tkips\\ \varphi \left(2.4dt{F}_u\right)=91.35tkips>81.59tkips\end{array}$

Therefore, use $\varphi R_n=81.59tkips/bolt$

Total connection strength = $2\left(24.35t\right)+6\left(24.35t\right)=170.5t$ (Shear controls)

Let $543.4t=170.5$

$t=0.3138in.$

Design top flange plate as a tension connection element

Tension on gross area:

Required $A_g=\frac{H}{0.90F_y}=\frac{147}{0.9\left(36\right)}=4.537in{.}^2$

Tension on net area:

Required $A_e=\frac{H}{0.75F_u}=\frac{147}{0.75\left(58\right)}=3.379in{.}^2$

Try a plate width of $w_g=7in.$

For gross area requirement,

$t=\frac{A_g}{w_g}=\frac{4.537}{7}=0.648in.$

For net area requirement,

Hole diameter = $\frac{7}{8}+\frac{1}{8}=1in.$

$t=\frac{A_n}{w_n}=\frac{A_n}{w_g-{\displaystyle \sum d_{hole}}}=\frac{3.379}{7-2\left(\frac{7}{8}+\frac{1}{8}\right)}=0.676in.$ (Controls)

Try a plate $\frac{3}{4}\times 7$

$A_n=\left[7-2\left(1.0\right)\right]\left(\frac{3}{4}\right)=3.75in{.}^2$

Check compression in the bottom plate:

Assume that the plate acts as a fixed-end compression member between the end fastener and the weld. Use $KL=0.65\left(1.5+0.5\right)=1.3in.$

$\begin{array}{l}r=\sqrt{\frac{I}{A}}=\sqrt{\frac{7{\left(5/8\right)}^3/12}{7\left(5/8\right)}}=0.1804in.\\ \frac{KL}{r}=\frac{1.3}{0.1804}=7.21\end{array}$

For compression elements with $\frac{KL}{r}<25$, the nominal strength is

$P_n=F_y{A}_g$

Therefore, $\varphi P_n=\varphi F_y{A}_g=0.9\left(36\right)\left(7\times \frac{3}{4}\right)=170kips>147kips$ (OK)

Check block shear on the plate using the dimensions and bolt layout shown.

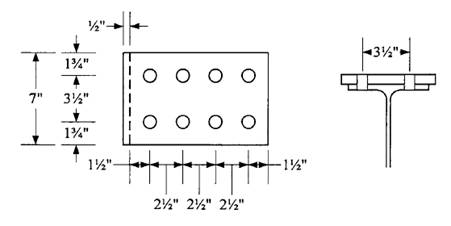
Shear areas:

$A_{gv}=\frac{3}{4}\left(9\right)\times 2=13.5in{.}^2$

$A_{nv}=\frac{3}{4}\left[9-3.5\left(1.0\right)\right]\times 2=8.25in{.}^2$ (3.5-hole diameters each side)

Tension area:

$A_{nt}=\frac{3}{4}\left[3.5-1\left(1.0\right)\right]=1.875in{.}^2$ (using $0.5+0.5$ hole diameters)

$\begin{array}{l}{R}_n=0.6F_u{A}_{nv}+U_{bs}{F}_u{A}_{nt}\\ =0.6\left(58\right)\left(8.25\right)+1.0\left(58\right)\left(1.875\right)=395.9kips\end{array}$

with an upper limit of

$0.6F_y{A}_{gv}+U_{bs}{F}_u{A}_{nt}=0.6\left(36\right)\left(13.5\right)+1.0\left(58\right)\left(1.875\right)=400.4kips$

The nominal block shear strength is therefore 395.9 kips. The design block shear strength is

$\varphi R_n=0.75\left(395.9\right)=297kips>147kips$ (OK)

Check block shear strength of beam flange:

Transverse spacing = gauge distance = 3.5 in.

Transverse edge distance = $\frac{6-3.5}{2}=1.25in.$

Longitudinal spacing and edge distance same as for plate.

Shear areas:

$\begin{array}{l}{A}_{gv}=0.425\left(9\right)\times 2=7.65in{.}^2\\ A_{nv}=0.425\left[9-3.5\left(1.0\right)\right]\times 2=4.675in{.}^2\end{array}$

Tension area:

$\begin{array}{l}{A}_{nt}=0.425\left[2.5-1\left(1.0\right)\right]=0.6375in{.}^2\\ R_n=0.6F_u{A}_{nv}+U_{bs}{F}_u{A}_{nt}\\ =0.6\left(58\right)\left(4.675\right)+1.0\left(58\right)\left(0.6375\right)=199.7kips\end{array}$

with an upper limit of

$0.6F_y{A}_{gv}+U_{bs}{F}_u{A}_{nt}=0.6\left(36\right)\left(7.65\right)+1.0\left(58\right)\left(0.6375\right)=202.2kips$

The nominal block shear strength is therefore 199.7 kips.

The design block shear strength is

$\varphi R_n=0.75\left(199.7\right)=149.8kips>147kips$ (OK)

Check beam for the effect of bolt holes in the tension flange:

The gross area of one flange is

$A_{fg}=t_f{b}_f=0.425\left(6.0\right)=2.55in{.}^2$

The effective hole diameter is

$\begin{array}{l}{d}_h=\frac{7}{8}+\frac{1}{8}=1in.\\ A_{fn}=A_{fg}-t_f{\displaystyle \sum d_h=2.55-0.425\left(2\times 1\right)}=1.7in{.}^2\\ F_u{A}_{fn}=65\left(1.7\right)=110.5kips\\ Y_t{F}_y{A}_{fg}=1.1\left(50\right)\left(2.55\right)=140.3kips\end{array}$

Since $F_u{A}_{fn}<Y_t{F}_y{A}_{fg}$, the holes must be accounted for.

$M_n=\frac{F_u{A}_{fn}}{A_{fg}}{S}_x=\frac{110.5}{2.55}\left(57.6\right)=2496in.-kips=208ft-kips$

${\varphi }_b{M}_n=0.90\left(208\right)=187ft-kips<216.8ft-kips$ (N.G.)

Try a smaller diameter bolt. Try ½-in. diameter bolts.

$A_b=\frac{\pi d^2}{4}=\frac{\pi {\left(\frac{1}{2}\right)}^2}{4}=0.1963in{.}^2$

Normal shearing strength = $\varphi R_n=0.75\left(54\right)\left(0.1963\right)=7.95kips/bolt$

Number of bolts required for shear is

$\frac{147}{7.95}=18.49$

Try 20 bolts (10 pair)

Bearing and block shear will be satisfactory.

Check reduction in beam flange area:

Use a hole diameter = $\frac{1}{2}+\frac{1}{8}=\frac{5}{8}in.$

$\begin{array}{l}{A}_{fn}=A_{fg}-t_f{\displaystyle \sum d_h=2.55-0.425\left(2\times \frac{5}{8}\right)=2.019in{.}^2}\\ F_u{A}_{fn}=65\left(2.019\right)=131.2kips\\ Y_t{F}_y{A}_{fg}=1.1\left(50\right)\left(2.55\right)=140.3kips\end{array}$

Since $F_u{A}_{fn}<Y_t{F}_y{A}_{fg}$, the holes must be accounted for.

$M_n=\frac{F_u{A}_{fn}}{A_{fg}}{S}_x=\frac{131.2}{2.55}\left(57.6\right)=2964in.-kips=247ft-kips$

${\varphi }_b{M}_n=0.90\left(247\right)=222.3ft-kips>216.8ft-kips$ (OK)

Plate length = $10\left(2.5\right)+1.5+1.5+0.5=28.5in.$

Conclusion:

Use a $PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$ with 20 bolts. For the web plate, use a $PL\frac{1}{4}\times 3\frac{1}{2}\times 10\frac{1}{2}$ with four 5/8-in. diameter Group A bolts as shown. Attach to column with a continuous 1/8-in. fillet weld on both sides of the plate. For each flange plate, use a $PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$ with twenty ½-in. diameter Group A bolts as shown.

To determine

(b)

The design of a three-plate moment connection of a $W18\times 35$ beam to a $W14\times 99$ column for the given conditions by using ASD

Answer to Problem 8.6.4P

$PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$with 20 bolts.

Use a $PL\frac{1}{4}\times 3\frac{1}{2}\times 10\frac{1}{2}$with four 5/8-in. diameter Group A bolts for the web plate.

1/8-in. fillet weld on both sides of the plate.

Use a $PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$with twenty ½-in. diameter Group A bolts for each flange plate.

Explanation of Solution

Given:

Service dead-load moment = 42 ft-kips

Service live-load moment = 104 ft-kips

Service dead-load beam reaction = 8 kips

Service live-load beam reaction = 21 kips

Group A bearing type bolts

E70 electrodes

A992 steel- Beam and column

A36 steel- Plate material

Calculation:

Reaction:

$R_a=D+L=8+21=29kips$

Moment:

$M_a=M_D+M_L=42+104=146ft-kips$

Web plate:

Neglect eccentricity.

Try 5/8-in. diameter bolts.

Assume that threads are in the plane of shear.

$A_b=\frac{\pi d^2}{4}=\frac{\pi {\left(5/8\right)}^2}{4}=0.3068in{.}^2$

Shear capacity of one bolt is

$\frac{R_n}{\Omega }=\frac{F_{nv}{A}_b}{\Omega }=\frac{54\left(0.3068\right)}{2.0}=8.28kips/bolt$

Number of bolts required is

$\frac{29}{8.28}=3.5$

Try 4 bolts.

Determine plate thickness required for bearing. Assume that

$\frac{R_n}{\Omega }=\frac{2.4dt{F}_u}{\Omega }=\frac{2.4\left(5/8\right)t\left(58\right)}{2.0}=43.5t$

Load resisted by each bolt = $\frac{29}{4}=7.25kips$

Let $\frac{R_n}{\Omega }=7.25=43.5t$

$t=0.167in.$

Try $t=\frac{3}{16}in.$

Determine whether plate or beam web controls bearing. For the plate,

$t{F}_u=\frac{3}{16}\left(58\right)=10.9kips/in.$

For the beam web, $t_w{F}_u=0.3\left(65\right)=19.5kips/in.>10.9kips/in.$

Therefore, plate controls.

Check bearing strength assumption:

$h=\frac{5}{8}+\frac{1}{16}=\frac{11}{16}in.$

For the hole nearest the edge, minimum $l_e=\frac{7}{8}in.$

Try $1\frac{1}{2}in.$

$\begin{array}{l}{l}_c=l_e-\frac{h}{2}=1.5-\frac{11/16}{2}=1.156in.\\ \frac{R_n}{\Omega }=\frac{1.2l_{c}t{F}_u}{\Omega }=\frac{1.2\left(1.156\right)\left(3/16\right)58}{2.0}=7.54kips\\ \frac{2.4dt{F}_u}{\Omega }=\frac{2.4\left(5/8\right)\left(3/16\right)58}{2.0}=8.156kips>7.54kips\end{array}$

Therefore, use $\frac{R_n}{\Omega }=7.54kips/bolt$

For other bolts, minimum $s=2.667\left(5/8\right)=1.667in.$

Use $s=2\frac{1}{2}in.$

$\begin{array}{l}{l}_c=s-h=2.5-\frac{11}{16}=1.813in.\\ \frac{R_n}{\Omega }=\frac{1.2l_{c}t{F}_u}{\Omega }=\frac{1.2\left(1.813\right)\left(3/16\right)\left(58\right)}{2.0}=11.83kips\\ \frac{2.4dt{F}_u}{\Omega }=8.156kips<11.83kips\end{array}$

Therefore, use $\frac{R_n}{\Omega }=8.156kips/bolt$

Bearing controls over shear at each bolt location.

Total strength is

$7.54+3\left(8.156\right)=32.008kips>29kips$ (OK)

Use four 5/8-in. diameter Group A bolts.

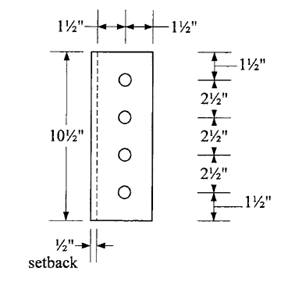
Determine plate thickness required for shear:

Shear yielding strength is

$\frac{R_n}{\Omega }=\frac{0.6F_y{A}_{gv}}{\Omega }$

Let $29=\frac{0.6\left(36\right)\left(10.5t\right)}{1.5}$

$t=0.192in.$

Try $t=\frac{1}{4}in.$

Check shear rupture strength:

Use hole diameter = $\frac{5}{8}+\frac{1}{8}=\frac{3}{4}in.$

$\begin{array}{l}{A}_{nv}=\left(10.5-4\times \frac{3}{4}\right)\frac{1}{4}=1.875in{.}^2\\ \frac{R_n}{\Omega }=\frac{0.6F_u{A}_{nv}}{\Omega }=\frac{0.6\left(58\right)\left(1.875\right)}{2.0}\end{array}$

$=32.625kips>29kips$ (OK)

Check block shear:

Shear areas:

$\begin{array}{l}{A}_{gv}=\frac{1.5+3\times 2.5}{4}=2.25in{.}^2\\ A_{nv}=\frac{9-3.5\left(3/4\right)}{4}=1.594in{.}^2\end{array}$

Tension area:

$\begin{array}{l}{A}_{nt}=\frac{1.5-0.5\left(3/4\right)}{4}=0.2813in{.}^2\\ R_n=0.6F_u{A}_{nv}+U_{bs}{F}_u{A}_{nt}\\ =0.6\left(58\right)\left(1.594\right)+1.0\left(58\right)\left(0.2813\right)=71.79kips\end{array}$

with an upper limit of

$0.6F_y{A}_{gv}+U_{bs}{F}_u{A}_{nt}=0.6\left(36\right)\left(2.25\right)+1.0\left(58\right)\left(0.2813\right)=64.92kips$

The nominal block shear strength is therefore 64.92 kips. The design block shear strength is

$\frac{R_n}{\Omega }=\frac{64.92}{2.0}=32.46kips>29kips$ (OK)

Use a $PL\frac{1}{4}\times 3\frac{1}{2}\times 10\frac{1}{2}$ as shown above.

Connection of shear plate to column flange:

Use E70 electrodes.

Minimum weld size, based on the plate thickness, is 1/8-in. try $w=\frac{1}{8}in.$

Weld strength = $1.392\times 2=2.784kips/in.$

Base metal (plate) shear strength:

The allowable shear yield strength per unit length is

$\frac{R_n}{\Omega }=\frac{0.6F_{y}t}{1.5}=0.4F_{y}t=0.4\left(36\right)\left(1/4\right)=3.6kips/in.>2.784kips/in.$

The base metal allowable shear rupture strength per unit length is

$\frac{R_n}{\Omega }=\frac{0.6F_{u}t}{2.0}=0.3F_{u}t=0.3\left(58\right)\left(1/4\right)=4.35kips/in.>2.784kips/in.$

Total length required = $\frac{29}{2.784}=10.42in.$

Use a continuous 1/8-in. fillet weld, both sides of plate.

Flange plate:

From $M=Hd$,

$H=\frac{M}{d}=\frac{146\left(12\right)}{17.7}=98.983kips$

Try 7/8-in. diameter bolts.

Assume that threads are in the plane of shear.

$\begin{array}{l}{A}_b=\frac{\pi {\left(7/8\right)}^2}{4}=0.6013in{.}^2\\ \frac{R_n}{\Omega }=\frac{54\left(0.6013\right)}{2.0}=16.235kips/bolt\end{array}$

Number of bolts required for shear is

$\frac{98.983}{16.235}=6.097$

Try 8 bolts (4 pair)

Determine plate thickness required for bearing:

$h=\frac{7}{8}+\frac{1}{16}=\frac{15}{16}in.$

Minimum $l_e=1\frac{1}{2}in.$

Use $1\frac{1}{2}in.$

Minimum $s=2.667\left(\frac{7}{8}\right)=2.33in.$

Use $2\frac{1}{2}in.$

For the hole nearest the edge,

$l_c=l_e-\frac{h}{2}=1.5-\frac{15/16}{2}=1.031in.$

$\begin{array}{l}\frac{R_n}{\Omega }=\frac{1.2l_{c}t{F}_u}{2.0}=\frac{1.2\left(1.031\right)t\left(58\right)}{2.0}=35.88tkips\\ \frac{2.4dt{F}_u}{\Omega }=\frac{1}{2.0}\left(2.4\right)\left(\frac{7}{8}\right)t\left(58\right)=60.9tkips>35.88tkips\end{array}$

Therefore, use $\frac{R_n}{\Omega }=35.88tkips/bolt$

For other bolts,

$\begin{array}{l}{l}_c=s-h=2.5-\frac{15}{16}=1.563in.\\ \frac{R_n}{\Omega }=\frac{1.2l_{c}t{F}_u}{2.0}=\frac{1.2\left(1.563\right)t\left(58\right)}{2.0}=54.4tkips\\ \frac{2.4dt{F}_u}{\Omega }=60.9tkips>54.4tkips\end{array}$

Therefore, use $\frac{R_n}{\Omega }=54.4tkips/bolt$

Total connection strength = $2\left(16.235t\right)+6\left(16.235t\right)=98.983$ (Shear controls)

Let $129.88t=98.983$

$t=0.762in.$

Design top flange plate as a tension connection element

Tension on gross area:

Required $A_g=\frac{1.67H}{F_y}=\frac{1.67\left(98.983\right)}{36}=4.592in{.}^2$

Tension on net area:

Required $A_e=\frac{2.0\left(H\right)}{F_u}=\frac{2.0\left(98.983\right)}{58}=3.413in{.}^2$

Try a plate width of $w_g=7in.$

For gross area requirement,

$t=\frac{A_g}{w_g}=\frac{4.592}{7}=0.656in.$

For net area requirement,

Hole diameter = $\frac{7}{8}+\frac{1}{8}=1in.$

$t=\frac{A_n}{w_n}=\frac{A_n}{w_g-{\displaystyle \sum d_{hole}}}=\frac{3.413}{7-2\left(\frac{7}{8}+\frac{1}{8}\right)}=0.6826in.$ (Controls)

Try a plate $\frac{3}{4}\times 7$

$A_n=\left[7-2\left(1.0\right)\right]\left(\frac{3}{4}\right)=3.75in{.}^2$

Check compression in the bottom plate:

Assume that the plate acts as a fixed-end compression member between the end fastener and the weld. Use $KL=0.65\left(1.5+0.5\right)=1.3in.$

$\begin{array}{l}r=\sqrt{\frac{I}{A}}=\sqrt{\frac{7{\left(5/8\right)}^3/12}{7\left(5/8\right)}}=0.1804in.\\ \frac{KL}{r}=\frac{1.3}{0.1804}=7.21\end{array}$

For compression elements with $\frac{KL}{r}<25$, the nominal strength is

$P_n=F_y{A}_g$

Therefore, $\frac{P_n}{\Omega }=\frac{F_y{A}_g}{1.67}=\frac{1}{1.67}\left(36\right)\left(7\times \frac{3}{4}\right)=113.17kips>98.983kips$ (OK)

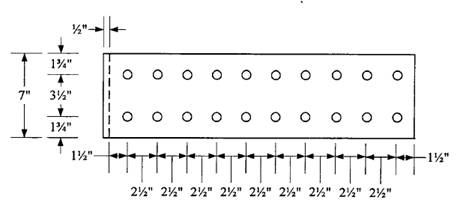
Check block shear on the plate using the dimensions and bolt layout shown.

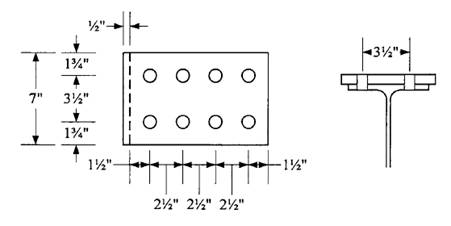
Shear areas:

$A_{gv}=\frac{3}{4}\left(9\right)\times 2=13.5in{.}^2$

$A_{nv}=\frac{3}{4}\left[9-3.5\left(1.0\right)\right]\times 2=8.25in{.}^2$ (3.5-hole diameters each side)

Tension area:

$A_{nt}=\frac{3}{4}\left[3.5-1\left(1.0\right)\right]=1.875in{.}^2$ (using $0.5+0.5$ hole diameters)

$\begin{array}{l}{R}_n=0.6F_u{A}_{nv}+U_{bs}{F}_u{A}_{nt}\\ =0.6\left(58\right)\left(8.25\right)+1.0\left(58\right)\left(1.875\right)=395.9kips\end{array}$

with an upper limit of

$0.6F_y{A}_{gv}+U_{bs}{F}_u{A}_{nt}=0.6\left(36\right)\left(13.5\right)+1.0\left(58\right)\left(1.875\right)=400.4kips$

The nominal block shear strength is therefore 395.9 kips. The design block shear strength is

$\frac{R_n}{\Omega }=\frac{395.9}{2.0}=197.95kips>98.983kips$ (OK)

Check block shear strength of beam flange:

Transverse spacing = gauge distance = 3.5 in.

Transverse edge distance = $\frac{6-3.5}{2}=1.25in.$

Longitudinal spacing and edge distance same as for plate.

Shear areas:

$\begin{array}{l}{A}_{gv}=0.425\left(9\right)\times 2=7.65in{.}^2\\ A_{nv}=0.425\left[9-3.5\left(1.0\right)\right]\times 2=4.675in{.}^2\end{array}$

Tension area:

$\begin{array}{l}{A}_{nt}=0.425\left[2.5-1\left(1.0\right)\right]=0.6375in{.}^2\\ R_n=0.6F_u{A}_{nv}+U_{bs}{F}_u{A}_{nt}\\ =0.6\left(58\right)\left(4.675\right)+1.0\left(58\right)\left(0.6375\right)=199.7kips\end{array}$

with an upper limit of

$0.6F_y{A}_{gv}+U_{bs}{F}_u{A}_{nt}=0.6\left(36\right)\left(7.65\right)+1.0\left(58\right)\left(0.6375\right)=202.2kips$

The nominal block shear strength is therefore 199.7 kips.

The design block shear strength is

$\frac{R_n}{\Omega }=\frac{199.7}{2.0}=99.85kips>98.983kips$ (OK)

Check beam for the effect of bolt holes in the tension flange:

The gross area of one flange is

$A_{fg}=t_f{b}_f=0.425\left(6.0\right)=2.55in{.}^2$

The effective hole diameter is

$\begin{array}{l}{d}_h=\frac{7}{8}+\frac{1}{8}=1in.\\ A_{fn}=A_{fg}-t_f{\displaystyle \sum d_h=2.55-0.425\left(2\times 1\right)}=1.7in{.}^2\\ F_u{A}_{fn}=65\left(1.7\right)=110.5kips\\ Y_t{F}_y{A}_{fg}=1.1\left(50\right)\left(2.55\right)=140.3kips\end{array}$

Since $F_u{A}_{fn}<Y_t{F}_y{A}_{fg}$, the holes must be accounted for.

$M_n=\frac{F_u{A}_{fn}}{A_{fg}}{S}_x=\frac{110.5}{2.55}\left(57.6\right)=2496in.-kips=208ft-kips$

$\frac{M_n}{{\Omega }_b}=\frac{208}{1.67}=124.55ft-kips<146ft-kips$ (N.G.)

Try a smaller diameter bolt. Try ½-in. diameter bolts.

$A_b=\frac{\pi d^2}{4}=\frac{\pi {\left(\frac{1}{2}\right)}^2}{4}=0.1963in{.}^2$

Normal shearing strength = $\frac{R_n}{\Omega }=\frac{54\left(0.1963\right)}{2.0}=5.3kips/bolt$

Number of bolts required for shear is

$\frac{98.983}{5.3}=18.7$

Try 20 bolts (10 pair)

Bearing and block shear will be satisfactory.

Check reduction in beam flange area:

Use a hole diameter = $\frac{1}{2}+\frac{1}{8}=\frac{5}{8}in.$

$\begin{array}{l}{A}_{fn}=A_{fg}-t_f{\displaystyle \sum d_h=2.55-0.425\left(2\times \frac{5}{8}\right)=2.019in{.}^2}\\ F_u{A}_{fn}=65\left(2.019\right)=131.2kips\\ Y_t{F}_y{A}_{fg}=1.1\left(50\right)\left(2.55\right)=140.3kips\end{array}$

Since $F_u{A}_{fn}<Y_t{F}_y{A}_{fg}$, the holes must be accounted for.

$M_n=\frac{F_u{A}_{fn}}{A_{fg}}{S}_x=\frac{131.2}{2.55}\left(57.6\right)=2964in.-kips=247ft-kips$

$\frac{M_n}{{\Omega }_b}=\frac{247}{1.67}=147.9ft-kips>146ft-kips$ (OK)

Plate length = $10\left(2.5\right)+1.5+1.5+0.5=28.5in.$

Conclusion:

Use a $PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$ with 20 bolts. For the web plate, use a $PL\frac{1}{4}\times 3\frac{1}{2}\times 10\frac{1}{2}$ with four 5/8-in. diameter Group A bolts as shown. Attach to column with a continuous 1/8-in. fillet weld on both sides of the plate. For each flange plate, use a $PL\frac{3}{4}\times 7\times 2^{\text{'}}-4{\frac{1}{2}}^{\text{'}\text{'}}$ with twenty ½-in. diameter Group A bolts as shown.