
A 1.00-kg object slides to the right on a surface having a coefficient of kinetic friction 0.250 (Fig. P8.62a). The object has a speed of vi = 3.00 m/s when it makes contact with a light spring (Fig. P8.62b) that has a force constant of 50.0 N/m. The object comes to rest after the spring has been compressed a distance d (Fig. P8.62c). The object is then forced toward the left by the spring (Fig. P8.62d) and continues to move in that direction beyond the spring's unstretched position. Finally, the object comes to rest a distance D to the left of the unstretched spring (Fig. P8.62e). Find (a) the distance of compression d, (b) the speed vat the unstretched posi-tion when the object is moving to the left (Fig. P8.624), and (c) the distance D where the abject comes to rest.
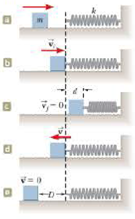
Figure P8.62
(a)
The distance of the compression.
Answer to Problem 8.62AP
The distance of the compression is
Explanation of Solution
Given info: The mass of the object is
The formula to calculate the change in energy is,
Here,
The formula to calculate the initial kinetic energy of the object is,
Here,
The formula to calculate the final kinetic energy is,
Here,
The formula to calculate initial potential energy is,
Here,
Thus the initial potential energy of the block is
The formula to calculate the final potential energy is,
Here,
Thus, the final potential energy of the block is
The formula to calculate the initial energy is,
Here,
Substitute
Thus, the initial energy is
The formula to calculate the final energy is,
Here,
Substitute
Thus, the final energy is
The formula to calculate the law of conservation of energy between the second and third diagram is,
Here,
Substitute
Substitute
Substitute
Further solve the above equation.
Conclusion:
Therefore, the distance of the compression is
(b)
The speed at the unstretched position when the object is moving to the left.
Answer to Problem 8.62AP
The speed at the unstretched position when the object is moving to the left is
Explanation of Solution
Given info: The mass of the object is
The formula to calculate the change in energy is,
Here,
The formula to calculate the law of conservation of energy between the second and fourth diagram is,
Here,
Substitute
Substitute
Substitute
Conclusion:
Therefore, the speed at the unstretched position when the object is moving to the left is
(c)
The distance where the object comes to rest.
Answer to Problem 8.62AP
The distance where the object comes to rest is
Explanation of Solution
Given info: The mass of the object is
The formula to calculate the change in energy is,
Here,
Thus, the value of change in energy is
The formula to calculate the law of conservation of energy between the second and fifth diagram is,
Here,
Substitute
Substitute
Substitute
Conclusion:
Therefore, the distance where the object comes to rest is
Want to see more full solutions like this?
Chapter 8 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Point charges q1 = 50 µC and q2 = −25 µC are placed 1.0 m apart. What is the magnitude of the force on a third charge q3 = 40 µC placed midway between q1 and q2? (The prefix µ =10−6 C.)arrow_forwardThe de-excitation of a state occurs by competing emission and relaxation processes. If the relaxation mechanisms are very effective:a) the emission of radiation is largeb) the emission of radiation is smallc) the emission occurs at a shorter wavelengthd) the de-excitation occurs only by emission processesarrow_forwardm C A block of mass m slides down a ramp of height hand collides with an identical block that is initially at rest. The two blocks stick together and travel around a loop of radius R without losing contact with the track. Point A is at the top of the loop, point B is at the end of a horizon- tal diameter, and point C is at the bottom of the loop, as shown in the figure above. Assume that friction between the track and blocks is negligible. (a) The dots below represent the two connected blocks at points A, B, and C. Draw free-body dia- grams showing and labeling the forces (not com ponents) exerted on the blocks at each position. Draw the relative lengths of all vectors to reflect the relative magnitude of the forces. Point A Point B Point C (b) For each of the following, derive an expression in terms of m, h, R, and fundamental constants. i. The speed of moving block at the bottom of the ramp, just before it contacts the stationary block ii. The speed of the two blocks immediately…arrow_forward
- The velocity of an elevator is given by the graph shown. Assume the positive direction is upward. Velocity (m/s) 3.0 2.5 2.0 1.5 1.0 0.5 0 0 5.0 10 15 20 25 Time (s) (a) Briefly describe the motion of the elevator. Justify your description with reference to the graph. (b) Assume the elevator starts from an initial position of y = 0 at t=0. Deriving any numerical values you need from the graph: i. Write an equation for the position as a function of time for the elevator from t=0 to t = 3.0 seconds. ii. Write an equation for the position as a function of time for the elevator from t = 3.0 seconds to t = 19 seconds. (c) A student of weight mg gets on the elevator and rides the elevator during the time interval shown in the graph. Consider the force of con- tact, F, between the floor and the student. How Justify your answer with reference to the graph does F compare to mg at the following times? and your equations above. i. = 1.0 s ii. = 10.0 sarrow_forwardStudents are asked to use circular motion to measure the coefficient of static friction between two materials. They have a round turntable with a surface made from one of the materials, for which they can vary the speed of rotation. They also have a small block of mass m made from the sec- ond material. A rough sketch of the apparatus is shown in the figure below. Additionally they have equipment normally found in a physics classroom. Axis m (a) Briefly describe a procedure that would allow you to use this apparatus to calculate the coefficient of static friction, u. (b) Based on your procedure, determine how to analyze the data collected to calculate the coefficient of friction. (c) One group of students collects the following data. r (m) fm (rev/s) 0.050 1.30 0.10 0.88 0.15 0.74 0.20 0.61 0.25 0.58 i. Use the empty spaces in the table as needed to calculate quantities that would allow you to use the slope of a line graph to calculate the coefficient of friction, providing labels with…arrow_forwardPART Aarrow_forward
- answer both questionarrow_forwardOnly part A.) of the questionarrow_forwardIn general it is best to conceptualize vectors as arrows in space, and then to make calculations with them using their components. (You must first specify a coordinate system in order to find the components of each arrow.) This problem gives you some practice with the components. Let vectors A = (1,0, -3), B = (-2, 5, 1), and C = (3,1,1). Calculate the following, and express your answers as ordered triplets of values separated by commas.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





