
Concept explainers
Draw the influence lines for the shear and bending moment at point B.
Draw the influence lines for the shear at internal hinge C.
Explanation of Solution
Calculation:
Influence line for shear at point B:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of frame as shown in Figure 1.
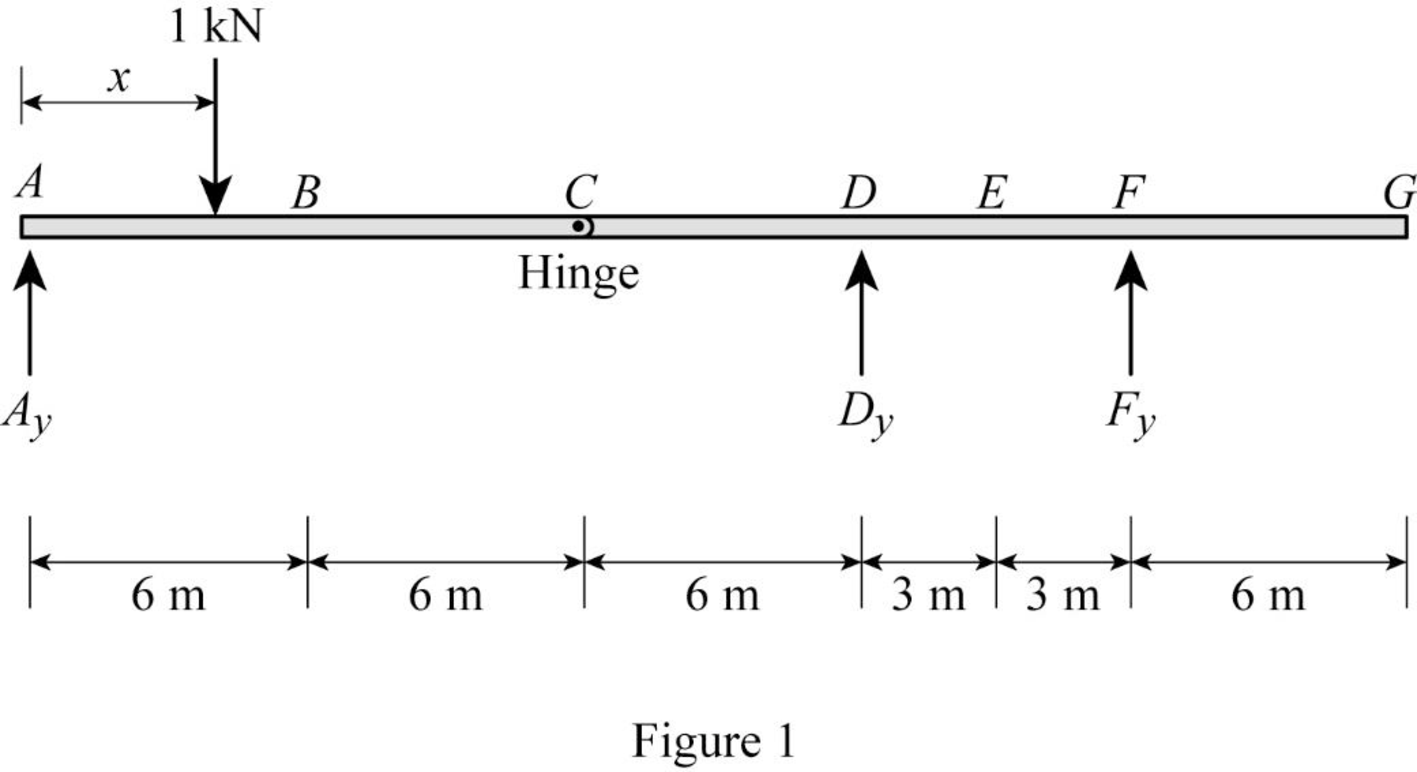
Refer Figure 1.
Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Apply moment equilibrium at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Consider the vertical forces equilibrium condition, take the upward force as positive
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Find the equation of shear at B of portion AB
Sketch the free body diagram of the section AB as shown in Figure 2.
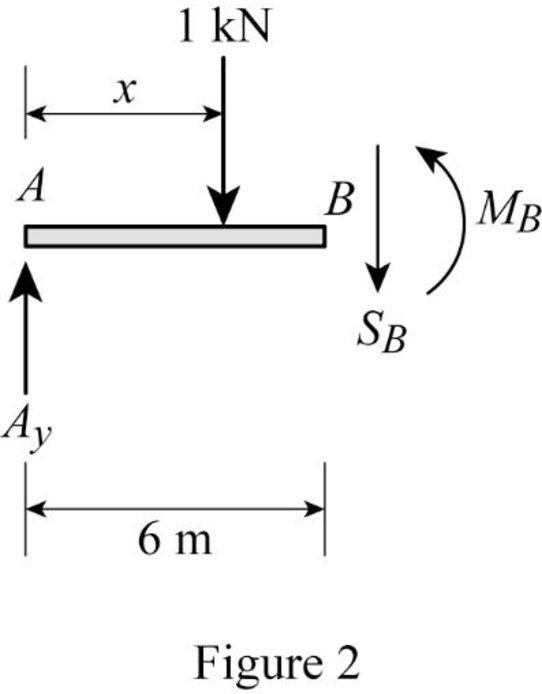
Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear at B of portion BG
Sketch the free body diagram of the section BG as shown in Figure 3.
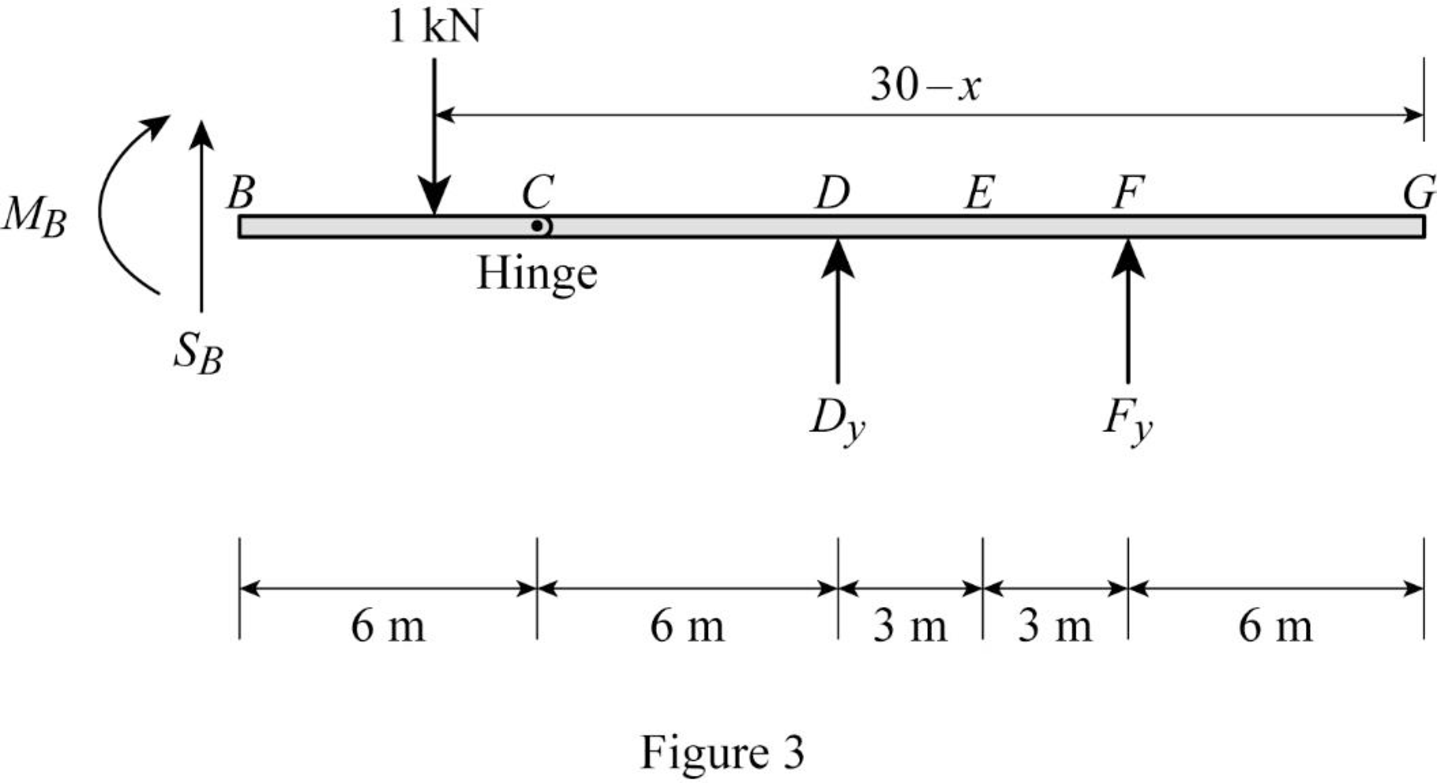
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive
Find the influence line ordinate of shear at B
Substitute
Find the influence line ordinate of shear at B
Substitute
Thus, the equations of the influence line ordinate for
Find the influence line ordinate of
| x (m) | Points | Influence line ordinate of |
| 0 | A | 0 |
| 6 | ‑0.5 | |
| 6 | 0.5 | |
| 12 | C | 0 |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
Sketch the influence line diagram for the shear at pointB as shown in Figure 4.

Influence line for moment at point B:
Refer Figure 2.
Find the equation of bending moment at B of portion AB
Take moment at B.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Refer Figure 3.
Find the equation of bending moment at B of portion BG
Take moment at B.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the influence line ordinate of moment at B
Substitute
Find the influence line ordinate of moment at B
Substitute
Thus, the equations of the influence line ordinate for
Find the influence line ordinate of
| x (m) | Points | Influence line ordinate of |
| 0 | A | 0 |
| 6 | ‑3 | |
| 12 | C | 0 |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
Sketch the influence line diagram for the bending moment at point B as shown in Figure 5.
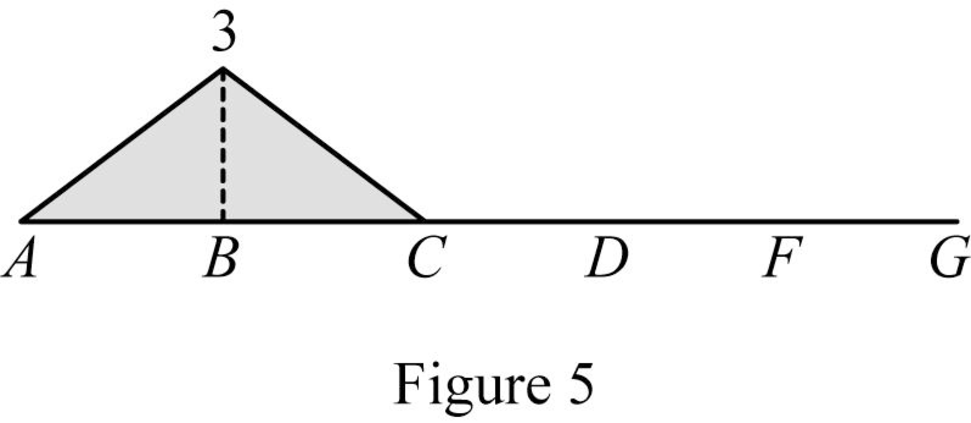
Influence line for shear at hinge C:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of frame as shown in Figure 6.
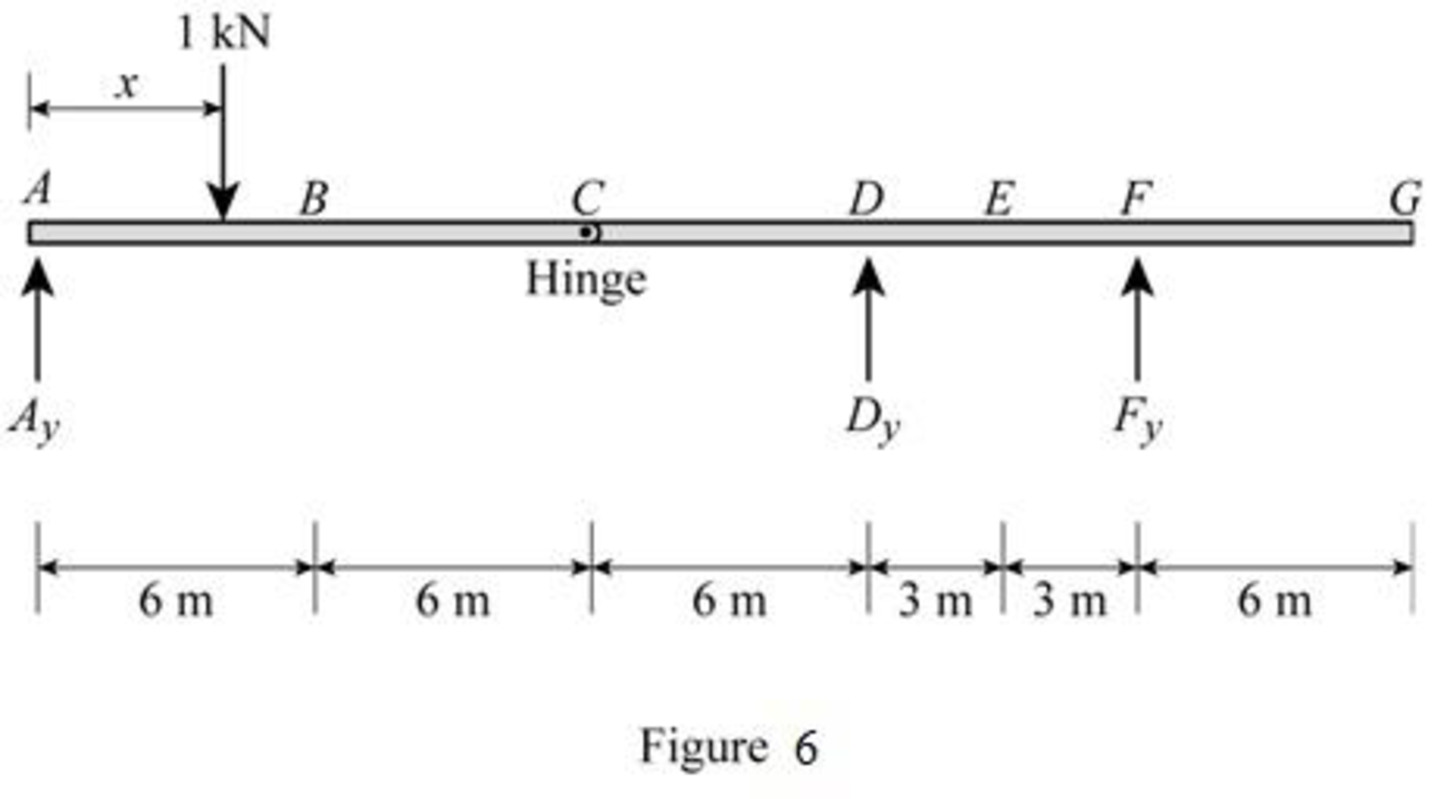
Refer Figure 6.
Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Apply moment equilibrium at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Consider the vertical forces equilibrium condition, take the upward force as positive
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Find the equation of shear at C of portion AC
Sketch the free body diagram of the section AC as shown in Figure 7.
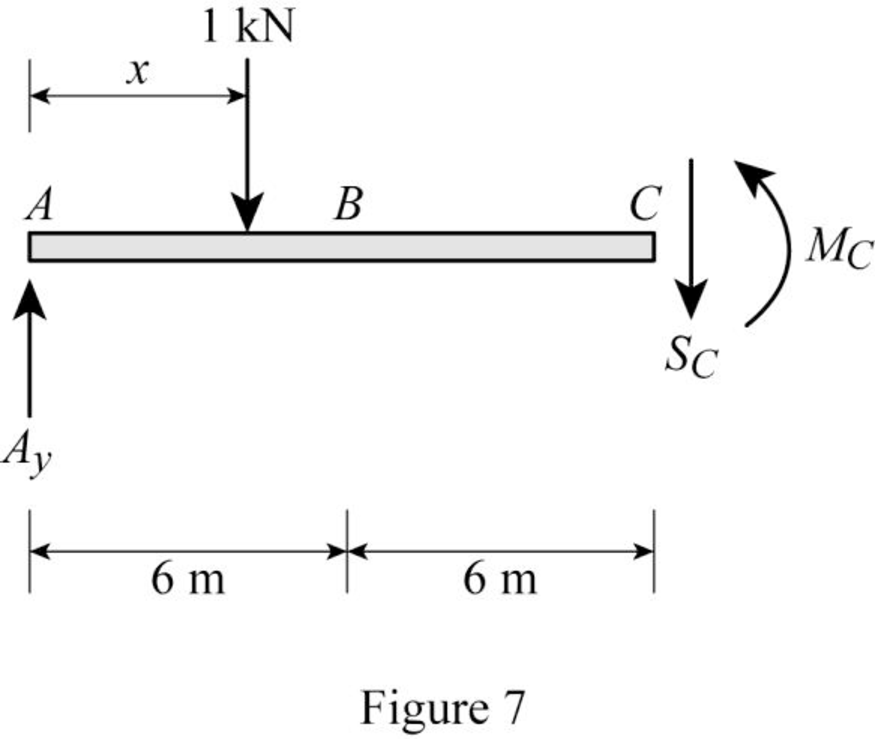
Refer Figure 7.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear at C of portion CG
Sketch the free body diagram of the section CG as shown in Figure 8.
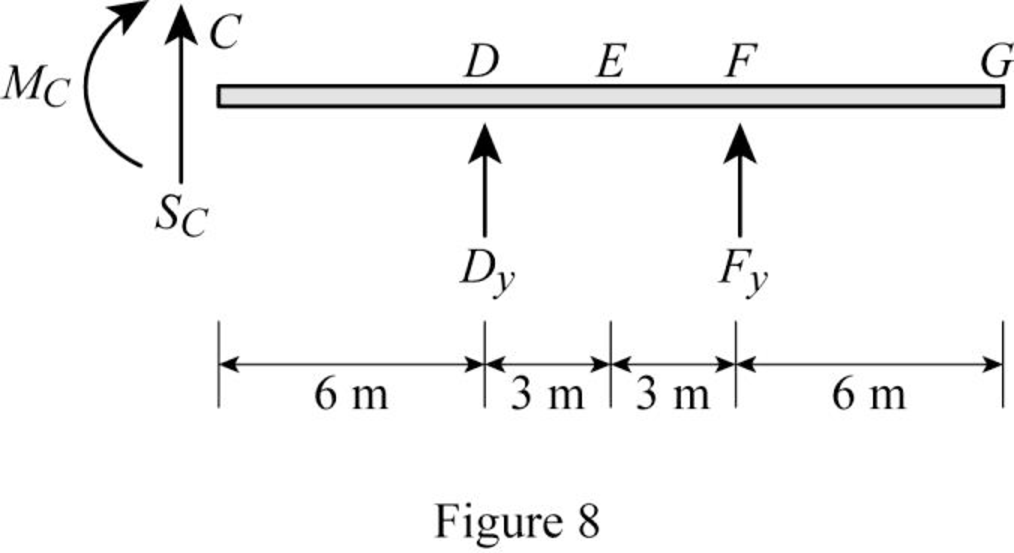
Refer Figure 8.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Thus, the equations of the influence line ordinate for
Find the influence line ordinate of
| x (m) | Points | Influence line ordinate of |
| 0 | A | 0 |
| 6 | ‑0.5 | |
| 12 | ‑1 | |
| 12 | 0 | |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
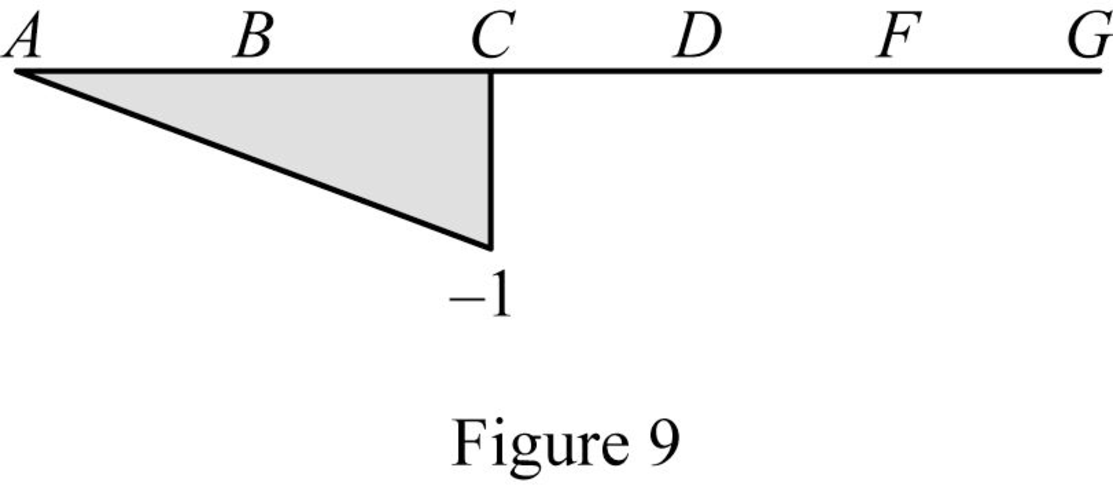
Sketch the influence line diagram for the shear at point C as shown in Figure 9.
Want to see more full solutions like this?
Chapter 8 Solutions
STRUCTURAL ANALYSIS (LL)
- A 2.0 m wide strip foundation carries a wall load of 350 kN/m in a clayey soil where y = 17 kN/m³, c' = 5.0 kN/m² and 23°. The foundation depth is 1.5 m. For o' = 23°: Nc = 18.05; N = 8.66; N = 8.20. Determine the factor of safety using the equation below. 1 qu = c' NcFcs Fed Fci +qNqFqs FqdFqi + ½ BN F√s 1 2 (Enter your answer to three significant figures.) s Fyd Fi FS =arrow_forward1.2 m BX B 70 kN.m y = 16 kN/m³ c' = 0 6'-30° Water table Ysat 19 kN/m³ c' 0 &' = 30° A square foundation is shown in the figure above. Use FS = 6, and determine the size of the foundation. Use the Prakash and Saran theory (see equation and figures below). Suppose that F = 450 kN. Qu = BL BL[c′Nc(e)Fcs(e) + qNg(e)Fcs(e) + · 1 YBN(e) F 2 7(e) Fra(e)] (Enter your answer to two significant figures.) B: m Na(e) 60 40- 20- e/B=0 0.1 0.2 0.3 .0.4 0 0 10 20 30 40 Friction angle, ' (deg) Figure 1 Variation of Na(e) with o' Ny(e) 60 40 20 e/B=0 0.3 0.1 0.2 0.4 0 0 10 20 30 40 Friction angle, ' (deg) Figure 2 Variation of Nye) with o'arrow_forwardK/S 46. (O المهمات الجديدة 0 المنتهية 12 المغـ ۱۱:۰۹ search ليس لديك اي مهمات ☐ ○ ☑arrow_forward
- I need help setti if this problem up and solving. I keep doing something wrong.arrow_forward1.0 m (Eccentricity in one direction only)=0.15 m Call 1.5 m x 1.5m Centerline An eccentrically loaded foundation is shown in the figure above. Use FS of 4 and determine the maximum allowable load that the foundation can carry if y = 18 kN/m³ and ' = 35°. Use Meyerhof's effective area method. For '=35°, N = 33.30 and Ny = 48.03. (Enter your answer to three significant figures.) Qall = kNarrow_forwardWhat are some advantages and disadvantages of using prefabrication in construction to improve efficiency and cut down on delays?arrow_forward
- PROBLEM:7–23. Determine the maximum shear stress acting in the beam at the critical section where the internal shear force is maximum. 3 kip/ft ΑΟ 6 ft DiC 0.75 in. 6 ft 6 in. 1 in. F [ 4 in. C 4 in. D 6 in. Fig of prob:7-23 1 in. 6 ft Barrow_forward7.60 This abrupt expansion is to be used to dissipate the high-energy flow of water in the 5-ft-diameter penstock. Assume α = 1.0 at all locations. a. What power (in horsepower) is lost through the expansion? b. If the pressure at section 1 is 5 psig, what is the pressure at section 2? c. What force is needed to hold the expansion in place? 5 ft V = 25 ft/s Problem 7.60 (2) 10 ftarrow_forward7.69 Assume that the head loss in the pipe is given by h₁ = 0.014(L/D) (V²/2g), where L is the length of pipe and D is the pipe diameter. Assume α = 1.0 at all locations. a. Determine the discharge of water through this system. b. Draw the HGL and the EGL for the system. c. Locate the point of maximum pressure. d. Locate the point of minimum pressure. e. Calculate the maximum and minimum pressures in the system. Elevation 100 m Water T = 10°C L = 100 m D = 60 cm Elevation 95 m Elevation 100 m L = 400 m D = 60 cm Elevation = 30 m Nozzle 30 cm diameter jet Problem 7.69arrow_forward
- A rectangular flume of planed timber (n=0.012) slopes 0.5 ft per 1000 ft. (i)Compute the discharge if the width is 7 ft and the depth of water is 3.5 ft. (ii) What would be thedischarge if the width were 3.5 ft and depth of water is 7 ft? (iii) Which of the two forms wouldhave greater capacity and which would require less lumber?arrow_forwardFigure shows a tunnel section on the Colorado River Aqueduct. The area of the water cross section is 191 ft 2 , and the wetted perimeter is 39.1 ft. The flow is 1600 cfs. If n=0.013 for the concrete lining, find the slope.arrow_forward7.48 An engineer is making an estimate for a home owner. This owner has a small stream (Q= 1.4 cfs, T = 40°F) that is located at an elevation H = 34 ft above the owner's residence. The owner is proposing to dam the stream, diverting the flow through a pipe (penstock). This flow will spin a hydraulic turbine, which in turn will drive a generator to produce electrical power. Estimate the maximum power in kilowatts that can be generated if there is no head loss and both the turbine and generator are 100% efficient. Also, estimate the power if the head loss is 5.5 ft, the turbine is 70% efficient, and the generator is 90% efficient. Penstock Turbine and generator Problem 7.48arrow_forward
