
For the digraph shown in Fig. 8-25, find
a. the indegree and outdegree of A.
b. the indegree and outdegree of B.
c. the indegree and outdegree of D.
d. the sum of the indegrees of all the vertices.
e. the sum of the outdegrees of all the vertices.
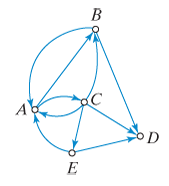
Figure 8-25
(a)
To find:
The in degree and out degree of A in the given digraph.
Answer to Problem 1E
Solution:
The in degree of A is 3 and out degree of A is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (1).
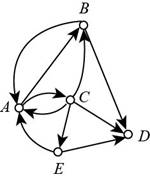
Figure (1)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (1) it can be noticed that there are 3 arcs having their ending vertex as A and 2 arcs having their starting vertex as A.
So, the indegree of A is 3 and outdegree of A is 2.
Conclusion:
Thus, the indegree of A is 3 and outdegree of A is 2.
(b)
To find:
The in degree and out degree of B in the given digraph.
Answer to Problem 1E
Solution:
The in degree of B is 2 and out degree of B is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (2).
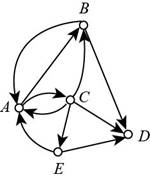
Figure (2)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (2) it can be noticed that there are 2 arcs having their ending vertex as B and 2 arcs having their starting vertex as B.
So, the indegree of B is 2 and outdegree of A is 2.
Conclusion:
Thus, the indegree of B is 2 and outdegree of B is 2.
(c)
To find:
The in degree and out degree of D in the given digraph.
Answer to Problem 1E
Solution:
The in degree of D is 3 and out degree of D is 0.
Explanation of Solution
Given:
The given digraph is shown in figure (3).
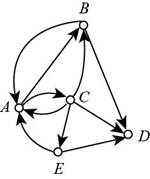
Figure (3)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (3) it can be noticed that there are 3 arcs having their ending vertex as D and no arc having their starting vertex as D.
So, the indegree of D is 3 and outdegree of D is 0.
Conclusion:
Thus, the indegree of D is 3 and outdegree of D is 0.
(d)
To find:
The sum of the in degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the indegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (4).

Figure (4)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (4) it can be noticed that there total 10 arcs, so there will be total 10 indegrees for all the vertices.
Conclusion:
Thus, the sum of all the indegrees is 10.
(e)
To find:
The sum of the out degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the outdegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (5).

Figure (5)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (5) it can be noticed that there total 10 arcs, so there will be total 10 outdegrees for all the vertices.
Conclusion:
Thus, the sum of all the outdegrees is 10.
Want to see more full solutions like this?
Chapter 8 Solutions
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
- Solve the equation. Write the smaller answer first. 2 (x-6)² = 36 x = Α x = Previous Page Next Pagearrow_forwardWrite a quadratic equation in factored form that has solutions of x = 2 and x = = -3/5 ○ a) (x-2)(5x + 3) = 0 ○ b) (x + 2)(3x-5) = 0 O c) (x + 2)(5x -3) = 0 ○ d) (x-2)(3x + 5) = 0arrow_forwardA vacant lot is being converted into a community garden. The garden and a walkway around its perimeter have an area of 690 square feet. Find the width of the walkway (x) if the garden measures 14 feet wide by 18 feet long. Write answer to 2 decimal places. (Write the number without units). Hint: add 2x to each of the garden dimensions of 14 x 18 feet to get the total area for the length multiplied by width.arrow_forward
- Solve the rational equation 14 1 + x-6 x x-7 x-7 ○ a) x = 1, x = 8 ○ b) x = 1 ○ c) x = 7 ○ d) x = 1, x = 7arrow_forwardSolve the absolute inequality | x + 5 > 3 ○ a) (-∞, -8] U[-2, ∞0) ☐ b) (-8, -2) c) (-2, ∞0) ○ d) (-∞, - 8) U(-2, ∞0)arrow_forward1) Listen Describe the error in the problem X 3 X x 3 - 2 = 25x = 0 25x 25 x = ±5arrow_forward

 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





