Chapter 7.FOM, Problem 1P

WAVE ON A CANAL A wave on the surface a long canal us described by the function

$y\left(x,t\right)=5\sin \left(2x-\frac{\pi }{2}t\right)$, $x\ge 0$

$\left(a\right)$ Find the function that models the positions of the point $x=0$ at any time $t$.

$\left(b\right)$ Sketch the shape of the wave when $t=0,0.4,0.8,1.2$ and $1.6$. Is this a travelling wave?

$\left(c\right)$ Find the velocity of the wave.

To determine

(a)

To find:

The function that models the positions of the point $x=0$ at any time $t$.

Answer to Problem 1P

Solution:

The function that models the position of the point $x=0$ at any time $t$ is $y\left(0,t\right)=-5\sin \left(\frac{\pi }{2}t\right)$.

Explanation of Solution

Given:

The equation of wave is $y\left(x,t\right)=5\sin \left(2x-\frac{\pi }{2}t\right)$.

Approach:

Substituting $x=0$ in equation of $y\left(x,t\right)=5\sin \left(2x-\frac{\pi }{2}t\right)$.

Here, $t$ is time, $x$ is space, $y$ is displacement.

Calculation:

The equation of wave is as follows.

$y\left(x,t\right)=5\sin \left(2x-\frac{\pi }{2}t\right)$

Substitute $0$ for $x$ in above equation.

$\begin{array}{rll}y\left(0,t\right)& =& 5\sin \left(2\times 0-\frac{\pi }{2}t\right)\\ & =& 5\sin \left(-\frac{\pi }{2}t\right)\end{array}$

Compare the above equation with standard equation $y\left(x,t\right)=A\sin \left(2x-2\pi t\right)$.

Here, $A=5$, $T=\frac{\pi }{2}$.

Therefore, the function that models the position of the point $x=0$ at any time $t$ is $y\left(0,t\right)=-5\sin \left(\frac{\pi }{2}t\right)$.

To determine

(b)

To sketch:

Shape of the wave when $t=0,0.4,0.8,1.2$ and $1.6$. Check whether it is travelling wave.

Answer to Problem 1P

Solution:

The graphs are shown below in figure $\left(1\right)$ and the given wave is a travelling wave.

Explanation of Solution

Approach:

Substitute $t=0,0.4,0.8,1.2$ and $1.6$ in equation $y\left(x,t\right)=5\sin \left(-\frac{\pi }{2}t\right)$.

Here, $t$ is time, $x$ is space and $y$ is displacement.

Calculation:

Write the given equation.

$y\left(x,t\right)=5\sin \left(2x-\frac{\pi }{2}t\right)$

Substitute $0,0.4,0.8,1.2$ and $1.6$ for $t$ in above equation as follows.

$y\left(x,0\right)=5\sin \left(2x-\frac{\pi }{2}\times 0\right)$

$y\left(x,0.4\right)=5\sin \left(2x-\frac{\pi }{2}\times 0.4\right)$

$y\left(x,0.8\right)=5\sin \left(2x-\frac{\pi }{2}\times 0.8\right)$

$y\left(x,1.2\right)=5\sin \left(2x-\frac{\pi }{2}\times 1.2\right)$

$y\left(x,1.6\right)=5\sin \left(2x-\frac{\pi }{2}\times 1.6\right)$

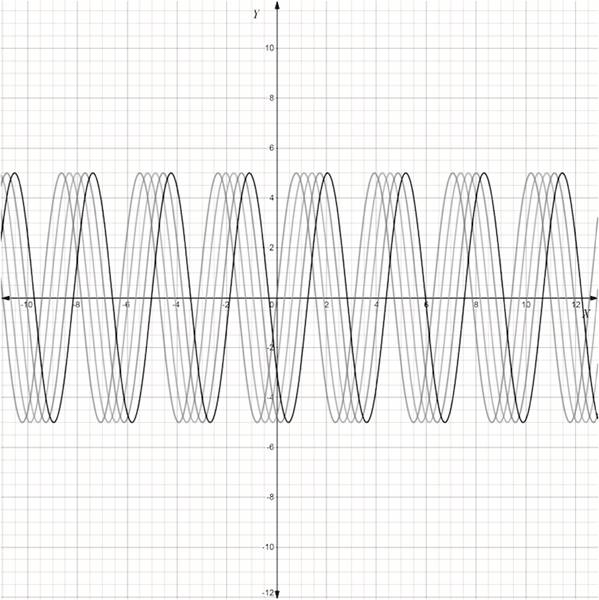
The graphs of $y\left(x,0\right)=5\sin \left(2x-\frac{\pi }{2}\times 0\right)$, $y\left(x,0.4\right)=5\sin \left(2x-\frac{\pi }{2}\times 0.4\right)$, $y\left(x,0.8\right)=5\sin \left(2x-\frac{\pi }{2}\times 0.8\right)$, $y\left(x,1.2\right)=5\sin \left(2x-\frac{\pi }{2}\times 1.2\right)$ and $y\left(x,1.6\right)=5\sin \left(2x-\frac{\pi }{2}\times 1.6\right)$ are shown in figure-$\left(1\right)$.

Figure $\left(1\right)$

Above figure is shifting with respect to time, thus it is a travelling wave.

Therefore, the graphs are shown above and the given wave is a travelling wave.

To determine

(c)

To find:

The velocity of the wave.

Answer to Problem 1P

Solution:

The velocity $v$ is $\frac{\pi }{4}$.

Explanation of Solution

Approach:

Compare the given equation with standard equation $y\left(x,t\right)=5\sin k\left(x-vt\right)$.

Calculation:

Write the given equation

$y\left(x,t\right)=5\sin \left(2x-\frac{\pi }{2}t\right)$

Take $2$ as common factor.

$y\left(x,t\right)=5\sin 2\left(x-\frac{\pi }{4}t\right)$

Compare the given equation with standard equation.

Here, $v=\frac{\pi }{4}$

Therefore, the velocity is $v=\frac{\pi }{4}$