Nature of Mathematics (MindTap Course List)
13th Edition
ISBN: 9781133947257
Author: karl J. smith
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 7.CR, Problem 1CR
To determine
(a)
To find:
The number of cubes painted on 4 sides.
Expert Solution
Answer to Problem 1CR
Solution:
0 cubes.
Explanation of Solution
Calculation:
Given a 4-cm cube painted green is cut into 64 1-cm cubes.
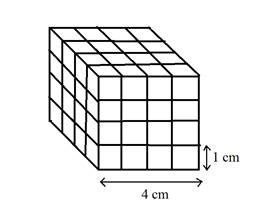
There will be no cube with all 4 sides painted on.
Final statement:
0 cubes will be painted on 4 sides.
To determine
(b)
To find:
The number of cubes painted on 3 sides.
Expert Solution
Answer to Problem 1CR
Solution:
8 cubes.
Explanation of Solution
Calculation:
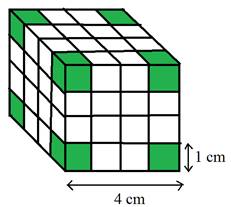
From the picture, the cubes painted on 3 sides are the cubes in the corner of the 4-cm cube.
The number of corners is 8.
Hence there are 8 cubes painted on 3 sides.
Final statement:
8 cubes will be painted on 3 sides.
To determine
(c)
To find:
The number of cubes painted on 2 sides.
Expert Solution
Answer to Problem 1CR
Solution:
24 cubes.
Explanation of Solution
Calculation:
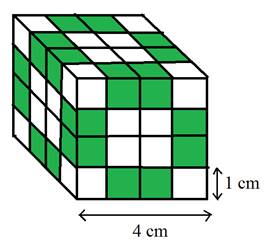
From the picture, the cubes painted on 2 sides are the cubes in the middle of the sides of the 4-cm cube.
There are 2 cubes in each side of the 4-cm cube.
The number of sides is 12.
The number of cubes is
Hence there are 24 cubes painted on 2 sides.
Final statement:
24 cubes will be painted on 2 sides.
To determine
(d)
To find:
The number of cubes painted on 1 side.
Expert Solution
Answer to Problem 1CR
Solution:
24 cubes.
Explanation of Solution
Calculation:
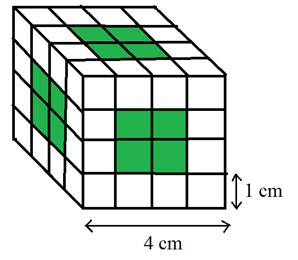
From the picture, the cubes painted on 1 side are the cubes in the middle of the faces of the 4-cm cube.
There are 4 cubes in each face of the 4-cm cube.
The number of faces is 6.
The number of cubes is
Hence there are 24 cubes painted on 1 side.
Final statement:
24 cubes will be painted on 1 side.
To determine
(e)
To find:
The number of cubes painted on 0 sides.
Expert Solution
Answer to Problem 1CR
Solution:
8 cubes.
Explanation of Solution
Calculation:
Total number of cubes is 64.
The number of cubes painted on 4 sides is 0.
The number of cubes painted on 3 sides is 8.
The number of cubes painted on 2 sides is 24.
The number of cubes painted on 1 side is 24.
Total number of painted cubes
The number of cubes painted on 0 sides is
Final statement:
8 cubes will be painted on 0 sides.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
added 2 images
Question 2: (10 points) Evaluate the definite integral.
Use the following form of the definition of the integral to evaluate the integral:
Theorem: Iff is integrable on [a, b], then
where Ax = (ba)/n and x₂ = a + i^x.
You might need the following formulas.
IM³
L² (3x²
(3x²+2x-
2x - 1)dx.
n
[f(z)dz lim f(x)Az
a
n→∞
i=1
n(n + 1)
2
n
i=1
n(n+1)(2n+1)
6
For the system consisting of the three planes:plane 1: -4x + 4y - 2z = -8plane 2: 2x + 2y + 4z = 20plane 3: -2x - 3y + z = -1a) Are any of the planes parallel and/or coincident? Justify your answer.b) Determine if the normals are coplanar. What does this tell you about the system?c) Solve the system if possible. Show a complete solution (do not use matrix operations). Classify the system using the terms: consistent, inconsistent, dependent and/or independent.
Chapter 7 Solutions
Nature of Mathematics (MindTap Course List)
Ch. 7.1 - Is the woman in the figure a young woman or an old...Ch. 7.1 - Is the fly in the Figure 7.11 on the cube or in...Ch. 7.1 - Prob. 3PSCh. 7.1 - Prob. 4PSCh. 7.1 - Prob. 5PSCh. 7.1 - Prob. 6PSCh. 7.1 - Prob. 7PSCh. 7.1 - Prob. 8PSCh. 7.1 - Prob. 9PSCh. 7.1 - Prob. 10PS
Ch. 7.1 - Prob. 11PSCh. 7.1 - Prob. 12PSCh. 7.1 - Prob. 13PSCh. 7.1 - Prob. 14PSCh. 7.1 - Prob. 15PSCh. 7.1 - Prob. 16PSCh. 7.1 - Prob. 17PSCh. 7.1 - Prob. 18PSCh. 7.1 - Use the illustration in Figure 7.12 to draw the...Ch. 7.1 - Prob. 20PSCh. 7.1 - Prob. 21PSCh. 7.1 - Prob. 22PSCh. 7.1 - Prob. 23PSCh. 7.1 - Prob. 24PSCh. 7.1 - Prob. 25PSCh. 7.1 - Prob. 26PSCh. 7.1 - Prob. 27PSCh. 7.1 - Carry out the constructions requested in Problems...Ch. 7.1 - Prob. 29PSCh. 7.1 - Prob. 30PSCh. 7.1 - Prob. 31PSCh. 7.1 - Prob. 32PSCh. 7.1 - Prob. 33PSCh. 7.1 - Prob. 34PSCh. 7.1 - Prob. 35PSCh. 7.1 - Prob. 36PSCh. 7.1 - Prob. 37PSCh. 7.1 - Prob. 38PSCh. 7.1 - Prob. 39PSCh. 7.1 - Prob. 40PSCh. 7.1 - Prob. 41PSCh. 7.1 - Prob. 42PSCh. 7.1 - Prob. 43PSCh. 7.1 - Prob. 44PSCh. 7.1 - Prob. 45PSCh. 7.1 - Prob. 46PSCh. 7.1 - Prob. 47PSCh. 7.1 - Prob. 48PSCh. 7.1 - Prob. 49PSCh. 7.1 - Prob. 50PSCh. 7.1 - Prob. 51PSCh. 7.1 - Study the patterns shown in Figure 7.13. When...Ch. 7.1 - Prob. 53PSCh. 7.1 - Prob. 54PSCh. 7.1 - Prob. 55PSCh. 7.1 - Prob. 56PSCh. 7.1 - Prob. 57PSCh. 7.1 - Prob. 58PSCh. 7.1 - The letters of the alphabet can be sorted into the...Ch. 7.1 - Prob. 60PSCh. 7.2 - Prob. 1PSCh. 7.2 - Prob. 2PSCh. 7.2 - Prob. 3PSCh. 7.2 - Prob. 4PSCh. 7.2 - Prob. 5PSCh. 7.2 - Prob. 6PSCh. 7.2 - Prob. 7PSCh. 7.2 - Prob. 8PSCh. 7.2 - Prob. 9PSCh. 7.2 - Prob. 10PSCh. 7.2 - Prob. 11PSCh. 7.2 - Prob. 12PSCh. 7.2 - Determine whether each sentence in Problems 11 14...Ch. 7.2 - Prob. 14PSCh. 7.2 - Prob. 15PSCh. 7.2 - Prob. 16PSCh. 7.2 - Prob. 17PSCh. 7.2 - Prob. 18PSCh. 7.2 - Prob. 19PSCh. 7.2 - Prob. 20PSCh. 7.2 - Prob. 21PSCh. 7.2 - Prob. 22PSCh. 7.2 - Prob. 23PSCh. 7.2 - Prob. 24PSCh. 7.2 - In Problems 25 32, classify the pairs of angles...Ch. 7.2 - Prob. 26PSCh. 7.2 - Prob. 27PSCh. 7.2 - Prob. 28PSCh. 7.2 - In Problems 25 32, classify the pairs of angles...Ch. 7.2 - Prob. 30PSCh. 7.2 - Prob. 31PSCh. 7.2 - Prob. 32PSCh. 7.2 - Prob. 33PSCh. 7.2 - Prob. 34PSCh. 7.2 - Prob. 35PSCh. 7.2 - Prob. 36PSCh. 7.2 - Prob. 37PSCh. 7.2 - Prob. 38PSCh. 7.2 - Prob. 39PSCh. 7.2 - Prob. 40PSCh. 7.2 - Prob. 41PSCh. 7.2 - Prob. 42PSCh. 7.2 - Prob. 43PSCh. 7.2 - Prob. 44PSCh. 7.2 - Prob. 45PSCh. 7.2 - Prob. 46PSCh. 7.2 - Prob. 47PSCh. 7.2 - Prob. 48PSCh. 7.2 - Prob. 49PSCh. 7.2 - Prob. 50PSCh. 7.2 - Prob. 51PSCh. 7.2 - In Problems 52 57, find the measures of all the...Ch. 7.2 - Prob. 53PSCh. 7.2 - Prob. 54PSCh. 7.2 - Prob. 55PSCh. 7.2 - Prob. 56PSCh. 7.2 - Prob. 57PSCh. 7.2 - Prob. 58PSCh. 7.2 - Prob. 59PSCh. 7.2 - Historical Quest: Allow me to start you on a...Ch. 7.3 - IN YOUR OWN WORDS What is a triangle?Ch. 7.3 - Prob. 2PSCh. 7.3 - IN YOUR OWN WORDS Explain the notation ABCDEF.Ch. 7.3 - Prob. 4PSCh. 7.3 - Prob. 5PSCh. 7.3 - Prob. 6PSCh. 7.3 - Prob. 7PSCh. 7.3 - Prob. 8PSCh. 7.3 - Prob. 9PSCh. 7.3 - Name the corresponding parts of the triangles in...Ch. 7.3 - In Problems 11-16, find the measure of the third...Ch. 7.3 - Prob. 12PSCh. 7.3 - Prob. 13PSCh. 7.3 - Prob. 14PSCh. 7.3 - Prob. 15PSCh. 7.3 - Prob. 16PSCh. 7.3 - Prob. 17PSCh. 7.3 - Prob. 18PSCh. 7.3 - Prob. 19PSCh. 7.3 - Prob. 20PSCh. 7.3 - Prob. 21PSCh. 7.3 - Prob. 22PSCh. 7.3 - Prob. 23PSCh. 7.3 - Prob. 24PSCh. 7.3 - Prob. 25PSCh. 7.3 - Prob. 26PSCh. 7.3 - Prob. 27PSCh. 7.3 - Prob. 28PSCh. 7.3 - Prob. 29PSCh. 7.3 - Prob. 30PSCh. 7.3 - Prob. 31PSCh. 7.3 - Prob. 32PSCh. 7.3 - Prob. 33PSCh. 7.3 - Prob. 34PSCh. 7.3 - Use algebra to find the value of x in each of the...Ch. 7.3 - Prob. 36PSCh. 7.3 - Prob. 37PSCh. 7.3 - Use algebra to find the value of x in each of the...Ch. 7.3 - Prob. 39PSCh. 7.3 - Prob. 40PSCh. 7.3 - Prob. 41PSCh. 7.3 - Prob. 42PSCh. 7.3 - Prob. 43PSCh. 7.3 - Prob. 44PSCh. 7.3 - Prob. 45PSCh. 7.3 - Prob. 46PSCh. 7.3 - Prob. 47PSCh. 7.3 - Prob. 48PSCh. 7.3 - Prob. 49PSCh. 7.3 - Prob. 50PSCh. 7.3 - Prob. 51PSCh. 7.3 - Prob. 52PSCh. 7.3 - Prob. 53PSCh. 7.3 - Prob. 54PSCh. 7.3 - Prob. 55PSCh. 7.3 - Prob. 56PSCh. 7.3 - The legs of a picnic table form a triangle where...Ch. 7.3 - Prob. 58PSCh. 7.3 - Prob. 59PSCh. 7.3 - Prob. 60PSCh. 7.4 - IN YOUR OWN WORDS Contrast congruent and similar...Ch. 7.4 - Prob. 2PSCh. 7.4 - In Problems 3-8, determine if the triangles are...Ch. 7.4 - Prob. 4PSCh. 7.4 - Prob. 5PSCh. 7.4 - Prob. 6PSCh. 7.4 - Prob. 7PSCh. 7.4 - Prob. 8PSCh. 7.4 - Prob. 9PSCh. 7.4 - Prob. 10PSCh. 7.4 - Prob. 11PSCh. 7.4 - Prob. 12PSCh. 7.4 - Prob. 13PSCh. 7.4 - Prob. 14PSCh. 7.4 - Prob. 15PSCh. 7.4 - Prob. 16PSCh. 7.4 - Prob. 17PSCh. 7.4 - Prob. 18PSCh. 7.4 - Prob. 19PSCh. 7.4 - Prob. 20PSCh. 7.4 - Prob. 21PSCh. 7.4 - Prob. 22PSCh. 7.4 - Prob. 23PSCh. 7.4 - Prob. 24PSCh. 7.4 - Prob. 25PSCh. 7.4 - Prob. 26PSCh. 7.4 - Prob. 27PSCh. 7.4 - Prob. 28PSCh. 7.4 - Prob. 29PSCh. 7.4 - Each figure in Problems 29-34 contains two similar...Ch. 7.4 - Prob. 31PSCh. 7.4 - Prob. 32PSCh. 7.4 - Prob. 33PSCh. 7.4 - Prob. 34PSCh. 7.4 - Prob. 35PSCh. 7.4 - Prob. 36PSCh. 7.4 - Given AC is perpendicular to MB, and ABC is an...Ch. 7.4 - Prob. 38PSCh. 7.4 - Prob. 39PSCh. 7.4 - Prob. 40PSCh. 7.4 - Use similar triangles and a proportion to find the...Ch. 7.4 - Prob. 42PSCh. 7.4 - Prob. 43PSCh. 7.4 - Prob. 44PSCh. 7.4 - Prob. 45PSCh. 7.4 - Prob. 46PSCh. 7.4 - A bell tower casts a shadow 45ft long. At the same...Ch. 7.4 - Prob. 48PSCh. 7.4 - Prob. 49PSCh. 7.4 - Prob. 50PSCh. 7.4 - Prob. 51PSCh. 7.4 - Prob. 52PSCh. 7.4 - Prob. 53PSCh. 7.4 - Prob. 54PSCh. 7.4 - Prob. 55PSCh. 7.4 - Suppose a 6- ft person wishes to determine the...Ch. 7.4 - Prob. 57PSCh. 7.4 - Prob. 58PSCh. 7.4 - Prob. 59PSCh. 7.4 - Prob. 60PSCh. 7.5 - Prob. 1PSCh. 7.5 - Prob. 2PSCh. 7.5 - Prob. 3PSCh. 7.5 - Prob. 4PSCh. 7.5 - Prob. 5PSCh. 7.5 - Prob. 6PSCh. 7.5 - Prob. 7PSCh. 7.5 - Prob. 8PSCh. 7.5 - Prob. 9PSCh. 7.5 - Prob. 10PSCh. 7.5 - Prob. 11PSCh. 7.5 - Prob. 12PSCh. 7.5 - Prob. 13PSCh. 7.5 - Prob. 14PSCh. 7.5 - Prob. 15PSCh. 7.5 - Prob. 16PSCh. 7.5 - Prob. 17PSCh. 7.5 - Prob. 18PSCh. 7.5 - Prob. 19PSCh. 7.5 - Prob. 20PSCh. 7.5 - Prob. 21PSCh. 7.5 - Prob. 22PSCh. 7.5 - Prob. 23PSCh. 7.5 - Prob. 24PSCh. 7.5 - Prob. 25PSCh. 7.5 - Prob. 26PSCh. 7.5 - Prob. 27PSCh. 7.5 - Prob. 28PSCh. 7.5 - Prob. 29PSCh. 7.5 - Prob. 30PSCh. 7.5 - Prob. 31PSCh. 7.5 - Prob. 32PSCh. 7.5 - Prob. 33PSCh. 7.5 - Prob. 34PSCh. 7.5 - Prob. 35PSCh. 7.5 - Prob. 36PSCh. 7.5 - Prob. 37PSCh. 7.5 - Prob. 38PSCh. 7.5 - Prob. 39PSCh. 7.5 - Prob. 40PSCh. 7.5 - Prob. 41PSCh. 7.5 - Prob. 42PSCh. 7.5 - Prob. 43PSCh. 7.5 - Prob. 44PSCh. 7.5 - Prob. 45PSCh. 7.5 - Prob. 46PSCh. 7.5 - Prob. 47PSCh. 7.5 - Level 2 If the angle from the horizontal to the...Ch. 7.5 - Prob. 49PSCh. 7.5 - Prob. 50PSCh. 7.5 - Prob. 51PSCh. 7.5 - Prob. 52PSCh. 7.5 - Prob. 53PSCh. 7.5 - Prob. 54PSCh. 7.5 - Prob. 55PSCh. 7.5 - Prob. 56PSCh. 7.5 - Prob. 57PSCh. 7.5 - Prob. 58PSCh. 7.5 - Prob. 59PSCh. 7.5 - Problem solving Level 3 a. If the distance from...Ch. 7.6 - Prob. 1PSCh. 7.6 - Prob. 2PSCh. 7.6 - Prob. 3PSCh. 7.6 - Prob. 4PSCh. 7.6 - Prob. 5PSCh. 7.6 - Prob. 6PSCh. 7.6 - Prob. 7PSCh. 7.6 - Prob. 8PSCh. 7.6 - Prob. 9PSCh. 7.6 - Prob. 10PSCh. 7.6 - Prob. 11PSCh. 7.6 - Prob. 12PSCh. 7.6 - Name the geometry Euclidean, elliptic, or...Ch. 7.6 - Prob. 14PSCh. 7.6 - Prob. 15PSCh. 7.6 - Prob. 16PSCh. 7.6 - Prob. 17PSCh. 7.6 - Prob. 18PSCh. 7.6 - Prob. 19PSCh. 7.6 - Prob. 20PSCh. 7.6 - Prob. 21PSCh. 7.6 - Prob. 22PSCh. 7.6 - Prob. 23PSCh. 7.6 - Prob. 24PSCh. 7.6 - Prob. 25PSCh. 7.6 - Prob. 26PSCh. 7.6 - Prob. 27PSCh. 7.6 - Prob. 28PSCh. 7.6 - Consider the top, front, and side views as shown...Ch. 7.6 - Prob. 30PSCh. 7.6 - Prob. 31PSCh. 7.6 - Prob. 32PSCh. 7.6 - Prob. 33PSCh. 7.6 - Prob. 34PSCh. 7.6 - Prob. 35PSCh. 7.6 - Prob. 36PSCh. 7.6 - Prob. 37PSCh. 7.6 - Prob. 38PSCh. 7.6 - Prob. 39PSCh. 7.6 - Prob. 40PSCh. 7.6 - Prob. 41PSCh. 7.6 - Prob. 42PSCh. 7.6 - Prob. 43PSCh. 7.6 - Prob. 44PSCh. 7.6 - Prob. 45PSCh. 7.6 - Prob. 46PSCh. 7.6 - Prob. 47PSCh. 7.6 - Prob. 48PSCh. 7.6 - Prob. 49PSCh. 7.6 - Prob. 50PSCh. 7.6 - Prob. 51PSCh. 7.6 - Prob. 52PSCh. 7.6 - Prob. 53PSCh. 7.6 - Prob. 54PSCh. 7.6 - When is an open book a closed book? If the...Ch. 7.6 - Prob. 56PSCh. 7.6 - Prob. 57PSCh. 7.6 - Prob. 58PSCh. 7.6 - Prob. 59PSCh. 7.CR - Prob. 1CRCh. 7.CR - Prob. 2CRCh. 7.CR - Prob. 3CRCh. 7.CR - Prob. 4CRCh. 7.CR - Prob. 5CRCh. 7.CR - Prob. 6CRCh. 7.CR - 7. Bourbon Palace Figure 7.77 is home to the...Ch. 7.CR - Prob. 8CRCh. 7.CR - Prob. 9CRCh. 7.CR - Prob. 10CRCh. 7.CR - Prob. 11CRCh. 7.CR - Prob. 12CRCh. 7.CR - Prob. 13CRCh. 7.CR - Prob. 14CRCh. 7.CR - Prob. 15CRCh. 7.CR - Prob. 16CRCh. 7.CR - Prob. 17CRCh. 7.CR - Prob. 18CRCh. 7.CR - Prob. 19CRCh. 7.CR - Prob. 20CR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- For the system consisting of the three planes:plane 1: -4x + 4y - 2z = -8plane 2: 2x + 2y + 4z = 20plane 3: -2x - 3y + z = -1a) Are any of the planes parallel and/or coincident? Justify your answer.b) Determine if the normals are coplanar. What does this tell you about the system?c) Solve the system if possible. Show a complete solution (do not use matrix operations). Classify the system using the terms: consistent, inconsistent, dependent and/or independent.arrow_forwardOpen your tool box and find geometric methods, symmetries of even and odd functions and the evaluation theorem. Use these to calculate the following definite integrals. Note that you should not use Riemann sums for this problem. (a) (4 pts) (b) (2 pts) 3 S³ 0 3-x+9-dz x3 + sin(x) x4 + cos(x) dx (c) (4 pts) L 1-|x|dxarrow_forwardA movie studio wishes to determine the relationship between the revenue generated from the streaming of comedies and the revenue generated from the theatrical release of such movies. The studio has the following bivariate data from a sample of fifteen comedies released over the past five years. These data give the revenue x from theatrical release (in millions of dollars) and the revenue y from streaming (in millions of dollars) for each of the fifteen movies. The data are displayed in the Figure 1 scatter plot. Theater revenue, x Streaming revenue, y (in millions of (in millions of dollars) dollars) 13.2 10.3 62.6 10.4 20.8 5.1 36.7 13.3 44.6 7.2 65.9 10.3 49.4 15.7 31.5 4.5 14.6 2.5 26.0 8.8 28.1 11.5 26.1 7.7 28.2 2.8 60.7 16.4 6.7 1.9 Streaming revenue (in millions of dollars) 18+ 16+ 14 12+ xx 10+ 8+ 6+ 2- 0 10 20 30 40 50 60 70 Theater revenue (in millions of dollars) Figure 1 Send data to calculator Send data to Excel The least-squares regression line for these data has a slope…arrow_forward
- 2arrow_forwardAn engineer is designing a pipeline which is supposed to connect two points P and S. The engineer decides to do it in three sections. The first section runs from point P to point Q, and costs $48 per mile to lay, the second section runs from point Q to point R and costs $54 per mile, the third runs from point R to point S and costs $44 per mile. Looking at the diagram below, you see that if you know the lengths marked x and y, then you know the positions of Q and R. Find the values of x and y which minimize the cost of the pipeline. Please show your answers to 4 decimal places. 2 Miles x = 1 Mile R 10 miles miles y = milesarrow_forwardhelp on this, results givenarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
ALGEBRAIC EXPRESSIONS & EQUATIONS | GRADE 6; Author: SheenaDoria;https://www.youtube.com/watch?v=fUOdon3y1hU;License: Standard YouTube License, CC-BY
Algebraic Expression And Manipulation For O Level; Author: Maths Solution;https://www.youtube.com/watch?v=MhTyodgnzNM;License: Standard YouTube License, CC-BY
Algebra for Beginners | Basics of Algebra; Author: Geek's Lesson;https://www.youtube.com/watch?v=PVoTRu3p6ug;License: Standard YouTube License, CC-BY
Introduction to Algebra | Algebra for Beginners | Math | LetsTute; Author: Let'stute;https://www.youtube.com/watch?v=VqfeXMinM0U;License: Standard YouTube License, CC-BY