THINKING MATHEMATICALLY W/ACCESS
19th Edition
ISBN: 9780135323038
Author: Blitzer
Publisher: Pearson Custom Publishing
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7.6, Problem 34E
The data can be modeled by
in which f(x} and g(x) represent the average cost of roomand hoard at public four-year colleges in the school year endingx years after 201b. Use these functions: to solve Exercises 33-34.
Where necessary, round answers to the nearest whole dollar.
34. a. According to the linear node], what was the averagecost of loom and board al public four-year colleges for the school year ending in 2015?
b. According to the exponential model, what was theaverage cost of room and board at public four-yearcolleges for the school year ending in 2015? $7629
c. Which function is a better model for the data for theschool year ending in 2015? the $$$ model
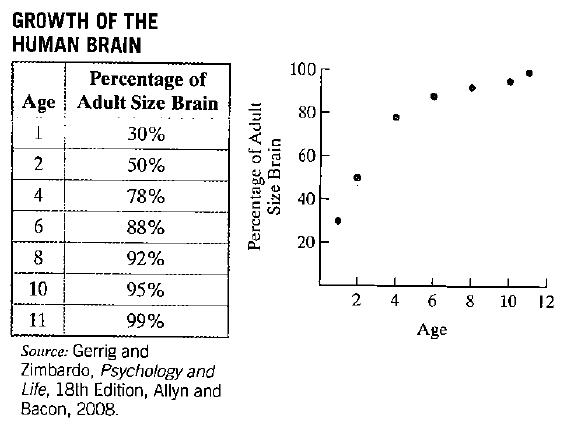
The data in the following table indicate that between the ages ofI and 11, the human brain does not grow linearly, or steadily. Ascatter pint for the data is shown to the right of the table.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please help ASAP on all asked questions. Please show all work and steps. Please circle the final answer.
Please help ASAP on all asked questions. Please show all work and steps. Please circle the final answer.
Please help ASAP on all asked questions. Please show all work and steps.
Chapter 7 Solutions
THINKING MATHEMATICALLY W/ACCESS
Ch. 7.1 - CHECK POINT 1 Plot the points: A ( − 2 , 4 ) , B (...Ch. 7.1 - CHECK POINT 2 Graph y = 4 − x . Select integers...Ch. 7.1 - CHECK POINT 3 The toll to a bridge costs $2. If...Ch. 7.1 - CHECK POINT 4 Find each of the following: a. f(6)...Ch. 7.1 - CHECK POINT 5 a. Use the line graph in Figure 7.7...Ch. 7.1 - CHECK POINT 6 Graph the functions f(x) = 2x and...Ch. 7.1 - Prob. 7CPCh. 7.1 - Prob. 8CPCh. 7.1 - Fill in each blank so that the resulting statement...Ch. 7.1 - Prob. 2CVC
Ch. 7.1 - Prob. 3CVCCh. 7.1 - Prob. 4CVCCh. 7.1 - Prob. 5CVCCh. 7.1 - Prob. 6CVCCh. 7.1 - If an equation in two variables (x and y) yields...Ch. 7.1 - Prob. 8CVCCh. 7.1 - Fill in each blank so that the resulting statement...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 11ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 24ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 27ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 29ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - Prob. 42ECh. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - Prob. 46ECh. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - Prob. 52ECh. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - Prob. 54ECh. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - Prob. 58ECh. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - Prob. 60ECh. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.1 - A football is thrown by a quarterback to a...Ch. 7.1 - Prob. 72ECh. 7.1 - Prob. 73ECh. 7.1 - Prob. 74ECh. 7.1 - Prob. 75ECh. 7.1 - Prob. 76ECh. 7.1 - The function G ( x ) = − 0.01 x 2 + x + 60 models...Ch. 7.1 - Prob. 78ECh. 7.1 - The function f ( x ) = 0.4 x 2 − 36 x + 1000...Ch. 7.1 - Prob. 80ECh. 7.1 - The function f ( x ) = 0.4 x 2 − 36 x + 1000...Ch. 7.1 - Prob. 82ECh. 7.1 - What is the rectangular coordinate system?Ch. 7.1 - Prob. 84ECh. 7.1 - Prob. 85ECh. 7.1 - Prob. 86ECh. 7.1 - Prob. 87ECh. 7.1 - Prob. 88ECh. 7.1 - Prob. 89ECh. 7.1 - Prob. 90ECh. 7.1 - Prob. 91ECh. 7.1 - Make Sense? In Exercises 89-92, determine whether...Ch. 7.1 - Prob. 93ECh. 7.1 - Prob. 94ECh. 7.1 - Prob. 95ECh. 7.1 - Prob. 96ECh. 7.1 - Use a graphing calculator to verify the graphs...Ch. 7.2 - CHECK POINT 1 Graph: 2 x + 3 y = 6.Ch. 7.2 - CHECK POINT 2 Find the slope of the line passing...Ch. 7.2 - Prob. 3CPCh. 7.2 - CHECK POINT 4 Graph the linear function by using...Ch. 7.2 - Prob. 5CPCh. 7.2 - CHECK POINT 6 Graph in the rectangular coordinate...Ch. 7.2 - CHECK POINT 7 Find the slope of the line segment...Ch. 7.2 - Prob. 8CPCh. 7.2 - The x-coordinate of a point where a graph crosses...Ch. 7.2 - The point (0, 3) lies along a line, so 3 is a/an...Ch. 7.2 - The slope of the line through the distinct points...Ch. 7.2 - Prob. 4CVCCh. 7.2 - The slope of the linear function whose equation is...Ch. 7.2 - 6. In order to graph the line whose equation is...Ch. 7.2 - Prob. 7CVCCh. 7.2 - Prob. 8CVCCh. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - Prob. 4ECh. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - Prob. 7ECh. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 10ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 12ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 14ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - Prob. 38ECh. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - Prob. 46ECh. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - 59. Older. Calmer. As we age, daily stress and...Ch. 7.2 - Prob. 60ECh. 7.2 - In Exercises 61-62, find a linear function in...Ch. 7.2 - Prob. 62ECh. 7.2 - Exercises 63-64 involve (he graphs of models for...Ch. 7.2 - Prob. 64ECh. 7.2 - Describe how to find the x-intercept of a linear...Ch. 7.2 - Prob. 66ECh. 7.2 - What is the slope of a line?Ch. 7.2 - Prob. 68ECh. 7.2 - Describe how to graph a line using the slope and...Ch. 7.2 - Prob. 70ECh. 7.2 - What does it mean if the slope of a line is...Ch. 7.2 - Prob. 72ECh. 7.2 - Prob. 73ECh. 7.2 - Prob. 74ECh. 7.2 - Make Sense? In Exercises 74-77, determine whether...Ch. 7.2 - Prob. 76ECh. 7.2 - Make Sense? In Exercises 74-77, determine whether...Ch. 7.2 - In Exercises 78-81, determine whether each...Ch. 7.2 - In Exercises 78-81, determine whether each...Ch. 7.2 - Prob. 80ECh. 7.2 - In Exercises 78-81, determine whether each...Ch. 7.2 - Prob. 82ECh. 7.2 - Prob. 83ECh. 7.2 - Use a graphing utility to verify any three of your...Ch. 7.3 - CHECK POINT 1 Determine whether ( − 4 , 3 ) is a...Ch. 7.3 - CHECK POINT 2 Solve by graphing: { 2 x + 3 y = 6 2...Ch. 7.3 - CHECK POINT 3 Solve by the substitution method: {...Ch. 7.3 - CHECK POINT 4 Solve by the substitution method:
Ch. 7.3 - CHECK POINT 5 Solve by the addition method: { 4 x...Ch. 7.3 - CHECK POINT 6 Solve by the addition method: { 3 x...Ch. 7.3 - CHECK POINT 7 Solve the system: { x + 2 y = ...Ch. 7.3 - CHECK POINT 8 Solve the system:
Ch. 7.3 - CHECK POINT 9 A company that manufactures running...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Prob. 5CVCCh. 7.3 - Prob. 6CVCCh. 7.3 - Prob. 7CVCCh. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - Prob. 8ECh. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - Prob. 14ECh. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - Prob. 16ECh. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13–24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - Prob. 36ECh. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - Prob. 40ECh. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - Prob. 44ECh. 7.3 - Use the graphs of the linear functions to solve...Ch. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - In Exercises 47-48, solve each system for x and y,...Ch. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - Prob. 52ECh. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - Prob. 56ECh. 7.3 - Exercises 57-60 describe a number of business...Ch. 7.3 - Prob. 58ECh. 7.3 - Exercises 57-60 describe a number of business...Ch. 7.3 - Prob. 60ECh. 7.3 - The able shows the price of a gallon of unleaded...Ch. 7.3 - Prob. 62ECh. 7.3 - We opened this section with a study showing that...Ch. 7.3 - 64. Harsh, mandatory minimum sentence for drug...Ch. 7.3 - 65. What is a system of linear equations? Provide...Ch. 7.3 - What is the solution to a system of linear...Ch. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - When is it easier to use the addition method...Ch. 7.3 - Prob. 72ECh. 7.3 - 73. When using the addition or substitution...Ch. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.3 - Prob. 81ECh. 7.4 - CHECK POINT 1 Graph: 2 x − 4 y ≥ 8.Ch. 7.4 - CHECK POINT 2 Graph: y > − 3 4 x .Ch. 7.4 - Prob. 3CPCh. 7.4 - Prob. 4CPCh. 7.4 - CHECK POINT 5 Graph the solution set of the...Ch. 7.4 - CHECK POINT 6 Graph the solution set of the...Ch. 7.4 - Prob. 1CVCCh. 7.4 - Fill in each blank so that the resulting statement...Ch. 7.4 - Prob. 3CVCCh. 7.4 - Prob. 4CVCCh. 7.4 - Prob. 5CVCCh. 7.4 - Prob. 6CVCCh. 7.4 - Prob. 7CVCCh. 7.4 - Prob. 8CVCCh. 7.4 - In Exercises 1-22, graph each linear inequality. x...Ch. 7.4 - Prob. 2ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 3...Ch. 7.4 - Prob. 4ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 2...Ch. 7.4 - Prob. 6ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 5...Ch. 7.4 - Prob. 8ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 2...Ch. 7.4 - Prob. 10ECh. 7.4 - In Exercises 1-22, graph each linear...Ch. 7.4 - Prob. 12ECh. 7.4 - In Exercises 1-22, graph each linear inequality. y...Ch. 7.4 - Prob. 14ECh. 7.4 - In Exercises 1-22, graph each linear...Ch. 7.4 - Prob. 16ECh. 7.4 - In Exercises 1-22, graph each linear...Ch. 7.4 - Prob. 18ECh. 7.4 - In Exercises 1-22, graph each linear inequality. y...Ch. 7.4 - Prob. 20ECh. 7.4 - In Exercises 1-22, graph each linear inequality. y...Ch. 7.4 - Prob. 22ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 26ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 30ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 32ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 34ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - 49. Many elevators have a capacity of 2000...Ch. 7.4 - Prob. 50ECh. 7.4 - In these graphs, each horizontal axis shows a...Ch. 7.4 - In these graphs, each horizontal axis shows a...Ch. 7.4 - What is a half-plane?Ch. 7.4 - What does a dashed line mean in the graph of an...Ch. 7.4 - Prob. 55ECh. 7.4 - Prob. 56ECh. 7.4 - Prob. 57ECh. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Prob. 62ECh. 7.4 - In Exercises 62-63, write a system of inequalities...Ch. 7.4 - Prob. 64ECh. 7.4 - Without graphing, in Exercises 64-67, determine if...Ch. 7.4 - Prob. 66ECh. 7.4 - Prob. 67ECh. 7.5 - CHECK POINT 1 A company manufactures bookshelves...Ch. 7.5 - CHECK POINT 2 To maintain high quality, the...Ch. 7.5 - CHECK POINT 3 To meet customer demand, the company...Ch. 7.5 - CHECK POINT 4 For the company in Check Points 1-3,...Ch. 7.5 - 1. A method for finding the maximum or minimum...Ch. 7.5 - 2. An algebraic expression in two or more...Ch. 7.5 - A system of linear inequalities is used to...Ch. 7.5 - In Exercises 1-4, find the value of the objective...Ch. 7.5 - Prob. 2ECh. 7.5 - In Exercises 1-4, find the value of the objective...Ch. 7.5 - Prob. 4ECh. 7.5 - In Exercises 5-8, an objective function and a...Ch. 7.5 - Prob. 6ECh. 7.5 - In Exercises 5-8, an objective function and a...Ch. 7.5 - In Exercises 5-8, an objective function and a...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - 13. a. A student earns $15 per hour for tutoring...Ch. 7.5 - 14. A television manufacturer makes...Ch. 7.5 - 15. Food and clothing are shipped to survivors of...Ch. 7.5 - Prob. 16ECh. 7.5 - 17. A theater is presenting a program on drinking...Ch. 7.5 - Prob. 18ECh. 7.5 - What kinds of problems are solved using the linear...Ch. 7.5 - Prob. 20ECh. 7.5 - Prob. 21ECh. 7.5 - Prob. 22ECh. 7.5 - Describe a situation in your life in which you...Ch. 7.5 - Prob. 24ECh. 7.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 7.5 - Prob. 26ECh. 7.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 7.5 - Prob. 28ECh. 7.5 - Group members should choose a particular field of...Ch. 7.5 - Members of the group should interview a business...Ch. 7.6 - CHECK POINT 1 Graph: f ( x ) = 3 x .Ch. 7.6 - CHECK POINT 2 Use the models f ( x ) = 0.074 x +...Ch. 7.6 - Prob. 3CPCh. 7.6 - Prob. 4CPCh. 7.6 - Prob. 5CPCh. 7.6 - Prob. 6CPCh. 7.6 - Prob. 7CPCh. 7.6 - Prob. 1CVCCh. 7.6 - Prob. 2CVCCh. 7.6 - Prob. 3CVCCh. 7.6 - For each set of points in Exercises 2-5, determine...Ch. 7.6 - Prob. 5CVCCh. 7.6 - 6. The exponential function with base b is defined...Ch. 7.6 - Prob. 7CVCCh. 7.6 - Prob. 8CVCCh. 7.6 - 9. is usually expressed as ______ and is called...Ch. 7.6 - Prob. 10CVCCh. 7.6 - Prob. 11CVCCh. 7.6 - In Exercises 1-6, use a table of coordinates to...Ch. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - In Exercises 1-6, use a table of coordinates to...Ch. 7.6 - Prob. 5ECh. 7.6 - Prob. 6ECh. 7.6 - Prob. 7ECh. 7.6 - Prob. 8ECh. 7.6 - In Exercises 9-14,
a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14,
a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 15-22,
a. Create a scatter plot for...Ch. 7.6 - Prob. 16ECh. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - In Exercises 15-22,
a. Create a scatter plot for...Ch. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - Prob. 20ECh. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - Prob. 22ECh. 7.6 - In Exercises 23-24, use a table of coordinates to...Ch. 7.6 - Prob. 24ECh. 7.6 - Prob. 25ECh. 7.6 - Prob. 26ECh. 7.6 - Prob. 27ECh. 7.6 - Prob. 28ECh. 7.6 - In Exercises 29-30, find the vertex for the...Ch. 7.6 - Prob. 30ECh. 7.6 - The graphing calculator screen displays an...Ch. 7.6 - The graphing calculator screen displays an...Ch. 7.6 - Prob. 33ECh. 7.6 - The data can be modeled by
in which f(x} and g(x)...Ch. 7.6 - The graphing calculator screen displays the...Ch. 7.6 - Prob. 36ECh. 7.6 - The percentage of adult height attained by a girl...Ch. 7.6 - The percentage of adult height attained by a girl...Ch. 7.6 - Prob. 39ECh. 7.6 - Prob. 40ECh. 7.6 - What is a scatter plot?Ch. 7.6 - Prob. 42ECh. 7.6 - Prob. 43ECh. 7.6 - Prob. 44ECh. 7.6 - Prob. 45ECh. 7.6 - Prob. 46ECh. 7.6 - Make Sense? In Exercises 47-50, determine whether...Ch. 7.6 - Prob. 48ECh. 7.6 - Prob. 49ECh. 7.6 - Prob. 50ECh. 7.6 - In Exercises 51-53, the value of a in y = a x 2 +...Ch. 7.6 - Prob. 52ECh. 7.6 - Prob. 53ECh. 7.6 - Prob. 54ECh. 7.6 - Prob. 55ECh. 7.6 - Each group member should consult an almanac,...Ch. 7 - In Exercises 1-4, plot the given point in a...Ch. 7 - In Exercises 1-4, plot the given point in a...Ch. 7 - Prob. 3RECh. 7 - In Exercises 1-4, plot the given point in a...Ch. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - In Exercises 14-15, use the vertical line test to...Ch. 7 - In Exercises 14-15, use the vertical line test to...Ch. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - In Exercises 20-23, calculate the slope of the...Ch. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - 34. Shown, again, is the scatter plot that...Ch. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - In Exercises 44-46, solve by the method of your...Ch. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 1TCh. 7 - Prob. 2TCh. 7 - Prob. 3TCh. 7 - Prob. 4TCh. 7 - Prob. 5TCh. 7 - Prob. 6TCh. 7 - Prob. 7TCh. 7 - Prob. 8TCh. 7 - Prob. 9TCh. 7 - Prob. 10TCh. 7 - Prob. 11TCh. 7 - Prob. 12TCh. 7 - Prob. 13TCh. 7 - Prob. 14TCh. 7 - Prob. 15TCh. 7 - Prob. 16TCh. 7 - Prob. 17TCh. 7 - Prob. 18TCh. 7 - Prob. 19TCh. 7 - Prob. 20TCh. 7 - Prob. 21TCh. 7 - Prob. 22TCh. 7 - Prob. 23TCh. 7 - Prob. 24TCh. 7 - Prob. 25TCh. 7 - Prob. 26TCh. 7 - Prob. 27TCh. 7 - Prob. 28TCh. 7 - Prob. 29TCh. 7 - Prob. 30T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Please help ASAP on all asked questions. Please show all work and steps. Please circle the final answer.arrow_forward8d6 عدد انباء Q/ Design a rectangular foo A ing of B-2.75m to support a column of dimensions (0.46 x 0.46) m, dead load =1300kN, live load = 1300kN, qa-210kPa, fc' 21 MPa, fy- 400 MPa. =arrow_forward5 of 5 (i) Let a discrete sample space be given by Ω = {ω1, 2, 3, 4}, Total marks 12 and let a probability measure P on be given by P(w1) 0.2, P(w2) = 0.2, P(w3) = 0.5, P(w4) = 0.1. = Consider the random variables X1, X2 → R defined by X₁(w3) = 1, X₁(4) = 1, X₁(w₁) = 1, X₁(w2) = 2, X2(w1) = 2, X2(w2) = 2, X2(W3) = 1, X2(w4) = 2. Find the joint distribution of X1, X2. (ii) [4 Marks] Let Y, Z be random variables on a probability space (N, F, P). Let the random vector (Y, Z) take on values in the set [0,1] × [0,2] and let the joint distribution of Y, Z on [0,1] × [0,2] be given by 1 dPy,z(y, z) (y²z + y²²) dy dz. Find the distribution Py of the random variable Y. [8 Marks]arrow_forward
- Refer to page 40 for solving a time-optimal control problem. Instructions: • Formulate the problem by minimizing the time to reach a target state. • Apply Pontryagin's Maximum Principle to derive the optimal control and switching conditions. • Solve explicitly for the control and state trajectories. Include clear diagrams to visualize the solution. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardQ1/ Two plate load tests were conducted in a C-0 soil as given belo Determine the required size of a footing to carry a load of 1250 kN for the same settlement of 30 mm. Size of plates (m) Load (KN) Settlement (mm) 0.3 x 0.3 40 30 0.6 x 0.6 100 30 Qx 0.6zarrow_forwardTotal marks 16 5. Let (,,P) be a probability space and let X : → R be a random variable whose probability density function is given by f(x) = }}|x|e¯|×| for x Є R. (i) (ii) Find the characteristic function of the random variable X. [8 Marks] Using the result of (i), calculate the first two moments of the random variable X, i.e., E(X") for n = 1, 2. (iii) What is the variance of X? [6 Marks] [2 Marks]arrow_forward
- Refer to page 12 for a problem on solving a homogeneous differential equation. Instructions: • Simplify the equation into a homogeneous form. Use appropriate substitutions to reduce complexity. Solve systematically and verify the final result with clear back-substitutions. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 36 for solving a bang-bang control problem. Instructions: • Formulate the problem, identifying the control constraints. • • Apply Pontryagin's Maximum Principle to derive the switching conditions. Clearly illustrate the switching points in the control trajectory. Verify the solution satisfies the optimality criteria. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardTotal marks 16 5. Let (N,F,P) be a probability space and let X : N → R be a random variable such that the probability density function is given by f(x)=ex for x € R. (i) Find the characteristic function of the random variable X. [8 Marks] (ii) Using the result of (i), calculate the first two moments of the random variable X, i.e., E(X") for n = 1,2. (iii) What is the variance of X. [6 Marks] [2 Marks]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY