
Concept explainers
For the beam and loading shown, (a) write the equations of the shear and bending-moment curves, (b) determine the magnitude and location of the maximum bending moment.
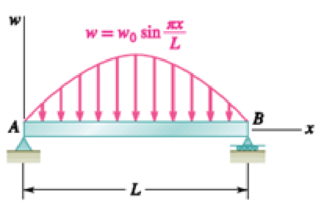
(a)
To write the equations of the shear and bending moment curves.
Answer to Problem 7.88P
The equation for shear curve is
Explanation of Solution
Refer Fig P7.88.
Write the equation for change in shear moment with distance.
Here,
Write the equation for change in bending moment with distance.
Here,
Conclusion:
Calculate the change in shear moment with distance using equation (I) and thus, find the equation for the shear moment curve.
Calculate the change in bending moment with distance using equation (II) and thus find the equation for the bending moment curve.
Apply boundary condition to find
At
Apply boundary condition to find
At
Use equation (V) to find the equation for shear curve.
Use equation (VI) to find the equation for bending moment curve.
Therefore, the equation for shear curve is
(b)
The magnitude and location of the maximum bending moment.
Answer to Problem 7.88P
The magnitude of the maximum bending moment is
Explanation of Solution
The maximum absolute value of the bending moment can be found using the equation for the bending moment curve.
Write the equation to find the maximum bending moment.
Conclusion:
Calculate the location of the maximum bending moment.
Calculate the maximum bending moment.
Therefore, the magnitude of the maximum bending moment is
Want to see more full solutions like this?
Chapter 7 Solutions
VECTOR MECHANICS FOR ENGINEERS: STATICS
- A mass of ideal gas in a closed piston-cylinder system expands from 427 °C and 16 bar following the process law, pv1.36 = Constant (p times v to the power of 1.36 equals to a constant). For the gas, initial : final pressure ratio is 4:1 and the initial gas volume is 0.14 m³. The specific heat of the gas at constant pressure, Cp = 0.987 kJ/kg-K and the specific gas constant, R = 0.267 kJ/kg.K. Determine the change in total internal energy in the gas during the expansion. Enter your numerical answer in the answer box below in KILO JOULES (not in Joules) but do not enter the units. (There is no expected number of decimal points or significant figures).arrow_forwardmy ID# 016948724. Please solve this problem step by steparrow_forwardMy ID# 016948724 please find the forces for Fx=0: fy=0: fz=0: please help me to solve this problem step by steparrow_forward
- My ID# 016948724 please solve the proble step by step find the forces fx=o: fy=0; fz=0; and find shear moment and the bending moment diagran please draw the diagram for the shear and bending momentarrow_forwardMy ID#016948724. Please help me to find the moment of inertia lx ly are a please show to solve step by stepsarrow_forwardplease solve this problem step by steparrow_forward
- Please do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning


