
Concept explainers
(b)
The null and alternative hypotheses for the consumption of proteins.
(b)
Answer to Problem 76E
Solution: The null and alternative hypotheses are formulated as
Explanation of Solution
Therefore, the hypotheses are formulated as:
In the above hypotheses
To find: The null and alternative hypotheses for the consumption of carbohydrates.
Answer to Problem 76E
Solution: The null and alternative hypotheses are formulated as
Explanation of Solution
Calculation: The significance test is to compare the two groups in terms of consumption of carbohydrates. Hence, the hypothesis is that the consumption of carbohydrates in the two groups is the same against the alternative that the consumption of carbohydrates in the two groups is not the same.
Therefore, the hypotheses are formulated as
In the above hypothesis
(c)
To find: The test statistic with the degrees of freedom and the p-value for consumption of proteins.
(c)
Answer to Problem 76E
Solution: The t – test statistic is obtained as 2.47 and p – value as 0.0144 for 199 degrees of freedom for consumption of proteins.
Explanation of Solution
Calculation: The two-sample t – test statistic for the hypothesis formulated in part (a) is defined as:
Where,
The difference of means is considered as 0 in the null hypothesis. Substitute the provided values in the above defined formula to compute the two sample t statistic. So,
The p-value for the provided one–sided test is calculated as
So, the degrees of freedom are 199. The Excel function to determine the p- value from t-test statistic is displayed in the attached screenshot,
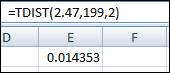
Therefore, the p-value is obtained as 0.0144.
To explain: The conclusion of the performed significance test.
Answer to Problem 76E
Solution: There is significant difference between the early eaters and late eaters in terms of consumption of proteins.
Explanation of Solution
To find: The test statistic with the degrees of freedom and the p-value for the consumption of carbohydrates.
Answer to Problem 76E
Solution: The t – test statistic is obtained as 0.29 and p – value as 0.772 for 199 degrees of freedom for carbohydrates consumption.
Explanation of Solution
Calculation: The two-sample t – test statistic for the hypothesis formulated in part (a) is defined as:
Where,
The difference of true means is considered as 0 according to the null hypothesis. Substitute the provided values in the above defined formula to compute the two sample t statistic. So,
The p-value for the provided one-sided test is calculated as
So, the degrees of freedom are 199. The Excel function to determine the p- value from t-test statistic is displayed in the attached screenshot,
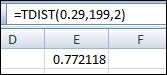
Therefore, the p-value is obtained as 0.772.
The conclusion of the performed significance test.
Answer to Problem 76E
Solution: There is no significant difference between the early eaters and late eaters in terms of consumption of carbohydrates.
Explanation of Solution
(d)
To find: A 95% confidence interval for the difference of means between early eaters and late eaters in terms of consumption of proteins.
(d)
Answer to Problem 76E
Solution: A required 95% confidence interval is
Explanation of Solution
Calculation: The formula for confidence interval for the difference between the means is defined as:
where
According to the Table D provided in the Appendix, the critical value for a two-tailed test at 95% confidence level is 1.962 for 199 degrees of freedom. Substitute the provided values in the above-defined formula to determine the 95% confidence interval for the difference between the early eaters and late eaters in terms of consumption of proteins. So,
Therefore, the 95% confidence interval for the difference between the means is obtained as
To explain: The comparison of information from the obtained confidence interval with the information given by the significance test.
Answer to Problem 76E
Solution: The information provided by both confidence interval and the significance test shows that there is a significant difference between the two means of proteins.
Explanation of Solution
To find: A 95% confidence interval for the difference of means between early eaters and late eaters in terms of consumption of carbohydrates.
Answer to Problem 76E
Solution: A required confidence interval is
Explanation of Solution
Calculation: The formula for confidence interval for the difference between the means is defined as:
where
According to the Table D provided in the Appendix, the critical value for a two-tailed test at 95% confidence level is 1.962 for 199 degrees of freedom. Substitute the provided values in the above defined formula to determine the 95% confidence interval for the difference between the early eaters and late eaters in terms of consumption of carbohydrates. So,
Interpretation: Therefore, the 95% confidence interval for the difference between the means is obtained as
To explain: The comparison of information from obtained confidence interval with the information given by the significance test.
Answer to Problem 76E
Solution: The information provided by both confidence interval and the significance test shows that there is no significant difference between the two means of carbohydrates.
Explanation of Solution
The obtained confidence interval
To explain: A short summary on the results of the performed significance test and obtained confidence intervals for three dietary compositions.
Answer to Problem 76E
Solution: From the calculated value of the test statistic from the previous exercise for the consumption of fats, the null hypothesis is not rejected and it is concluded that there is no significant difference between the consumption of fats. The obtained confidence interval
Explanation of Solution
From the calculated value of the test statistic for the consumption of proteins, the null hypothesis is rejected and it is concluded that there is a significant difference between the consumption of proteins. The obtained confidence interval
From the calculated value of the test statistic for the consumption of carbohydrates, the null hypothesis is not rejected and it is concluded that there is no significant difference between the consumption of carbohydrates. The obtained confidence interval
Want to see more full solutions like this?
Chapter 7 Solutions
LaunchPad for Moore's Introduction to the Practice of Statistics (12 month access)
- 2. Hypothesis Testing - Two Sample Means A nutritionist is investigating the effect of two different diet programs, A and B, on weight loss. Two independent samples of adults were randomly assigned to each diet for 12 weeks. The weight losses (in kg) are normally distributed. Sample A: n = 35, 4.8, s = 1.2 Sample B: n=40, 4.3, 8 = 1.0 Questions: a) State the null and alternative hypotheses to test whether there is a significant difference in mean weight loss between the two diet programs. b) Perform a hypothesis test at the 5% significance level and interpret the result. c) Compute a 95% confidence interval for the difference in means and interpret it. d) Discuss assumptions of this test and explain how violations of these assumptions could impact the results.arrow_forward1. Sampling Distribution and the Central Limit Theorem A company produces batteries with a mean lifetime of 300 hours and a standard deviation of 50 hours. The lifetimes are not normally distributed—they are right-skewed due to some batteries lasting unusually long. Suppose a quality control analyst selects a random sample of 64 batteries from a large production batch. Questions: a) Explain whether the distribution of sample means will be approximately normal. Justify your answer using the Central Limit Theorem. b) Compute the mean and standard deviation of the sampling distribution of the sample mean. c) What is the probability that the sample mean lifetime of the 64 batteries exceeds 310 hours? d) Discuss how the sample size affects the shape and variability of the sampling distribution.arrow_forwardA biologist is investigating the effect of potential plant hormones by treating 20 stem segments. At the end of the observation period he computes the following length averages: Compound X = 1.18 Compound Y = 1.17 Based on these mean values he concludes that there are no treatment differences. 1) Are you satisfied with his conclusion? Why or why not? 2) If he asked you for help in analyzing these data, what statistical method would you suggest that he use to come to a meaningful conclusion about his data and why? 3) Are there any other questions you would ask him regarding his experiment, data collection, and analysis methods?arrow_forward
- Businessarrow_forwardWhat is the solution and answer to question?arrow_forwardTo: [Boss's Name] From: Nathaniel D Sain Date: 4/5/2025 Subject: Decision Analysis for Business Scenario Introduction to the Business Scenario Our delivery services business has been experiencing steady growth, leading to an increased demand for faster and more efficient deliveries. To meet this demand, we must decide on the best strategy to expand our fleet. The three possible alternatives under consideration are purchasing new delivery vehicles, leasing vehicles, or partnering with third-party drivers. The decision must account for various external factors, including fuel price fluctuations, demand stability, and competition growth, which we categorize as the states of nature. Each alternative presents unique advantages and challenges, and our goal is to select the most viable option using a structured decision-making approach. Alternatives and States of Nature The three alternatives for fleet expansion were chosen based on their cost implications, operational efficiency, and…arrow_forward
- The following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8arrow_forwardII Consider the following data matrix X: X1 X2 0.5 0.4 0.2 0.5 0.5 0.5 10.3 10 10.1 10.4 10.1 10.5 What will the resulting clusters be when using the k-Means method with k = 2. In your own words, explain why this result is indeed expected, i.e. why this clustering minimises the ESS map.arrow_forwardwhy the answer is 3 and 10?arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





