
Concept explainers
(a)
To test: Whether the ‘friends on Facebook’ data is skewed or not by using appropriate graph.
(a)
Answer to Problem 26E
Solution: The data is positively skewed.
Explanation of Solution
Graph: To find whether data is skewed or not, the histogram can be drawn. To draw the histogram, follow the below mentioned steps in Minitab;
Step 1: Enter the data in Minitab and enter variable name as ‘Number of Facebook friend’.
Step 2: Go to
Step 3: In dialog box that appears select ‘friends on Facebook’ under the field marked as ‘Graph variable’. Then click Ok.
The histogram is as follows;
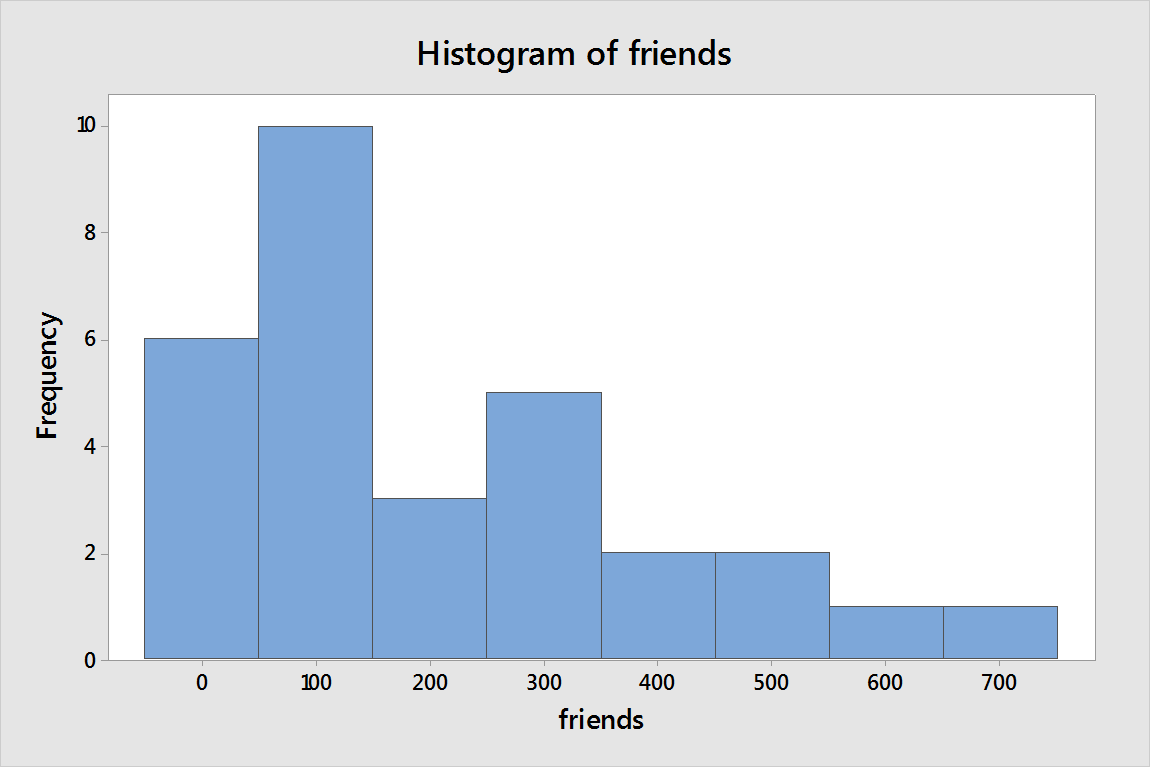
Conclusion: In above graph, it can be seen that most of the frequencies are distributed in right hand side of the highest frequency. Hence, the data is positively skewed.
To explain: The findings.
Answer to Problem 26E
Solution: The
Explanation of Solution
The most frequent any value is between 100 and 200 and most of the frequencies are distributed on the right hand side of this so the distribution is positively skewed.
(b)
To explain: Whether t method should be used to calculate 95% confidence interval for
(b)
Answer to Problem 26E
Solution: No, t method should be used to calculate confidence interval.
Explanation of Solution
There is an assumption for using t test that the population distribution must be
(c)
Section 1:
To find: The mean number of Facebook friends for sample.
(c)
Section 1:
Answer to Problem 26E
Solution: The sample mean is 205.3 (approximated to 205) friends.
Explanation of Solution
Calculation: To calculate the sample mean follow the below mentioned steps in Minitab;
Step 1: Enter the data in Minitab and enter variable name as ‘Number of Facebook friends’.
Step 2: Go to
Step 3: In dialog box that appears select ‘friends’ under the field marked as ‘Variables’. Then click on ‘Statistics’.
Step 4: In dialog box that appears select ‘None’ and then ‘Mean’. Finally click ‘Ok’ on both dialog boxes.
From Minitab result, the mean is 205.3 but number of friends is an integer value. So mean can never be a decimal value. Therefore, the nearest integer value will be 205. Hence the mean number of friend will be 205 friends.
Section 2:
To find: The standard deviation of Facebook friends for sample.
Section 2:
Answer to Problem 26E
Solution: The standard deviation is 196.3 (approximated to 196) friends.
Explanation of Solution
Calculation: To calculate the standard deviation follow the below mentioned steps in Minitab;
Step 1: Follow the step 1 to 3 performed in section 1 of part (b).
Step 2: In dialog box that appears select ‘None’ and then ‘standard deviation’. Finally click ‘Ok’ on both dialog boxes.
From Minitab result, the standard deviation is196.3 friends but number of friends is an integer value. So it can never be a decimal value and the nearest integer value will be 196. Hence the standard deviation of the number of friends will be 196 friends.
Section 3:
To find: The standard error of Facebook friends for sample.
Section 3:
Answer to Problem 26E
Solution: The standard error is 35.8 (approximated to 36) friends.
Explanation of Solution
Calculation: To calculate the standard error follow the below mentioned steps in Minitab;
Step 1: Follow the step 1 to 3 performed in section 1 of part (b).
Step 2: In dialog box that appears select ‘None’ and then ‘SE of mean’. Finally, click ‘Ok’ on both dialog boxes.
From Minitab result, the standard error is35.8 friends but the number of friends is an integer value. So the standard error can never be a decimal value. Therefore, the nearest integer value will be 36. Hence the standard deviation of the number of friends will be 36 friends.
Section 4:
To find: The margin of error for Facebook friends.
Section 4:
Answer to Problem 26E
Solution: The margin of error is 110.005 (approximated to 110) friends.
Explanation of Solution
Calculation: The formula to calculate the margin of error is as follows,
Where
Hence the margin of error is73.2996 friends but the number of friends is an integer value. So the standard error can never be a decimal value. Therefore, the nearest integer value will be 73. Hence the margin of error will be 73 friends.
(d)
To find: 95% confidence interval for data of friends on Facebook.
(d)
Answer to Problem 26E
Solution: The required confidence interval is
Explanation of Solution
Calculation: The confidence interval is an interval for which there is 95% chances that it contains the population parameter (population mean).
To calculate confidence interval, follow the below mentioned steps in Minitab;
Step 1: Enter the provided data into Minitab and enter variable name as ‘Number of Facebook friend’.
Step 2: Go to
Step 3: In the dialog box that appears select ‘Number of Facebook friends’ under the field marked as ‘Sample in columns’. Click on ‘option’.
Step 4: In the dialog box that appears, enter ‘95.0’ under the field marked as ‘Confidence level’ and select ‘not equal’ in ‘Alternative hypothesis’.
From Minitab results 95% confidence interval is (132.0, 278.6) . but the number of friends is an integer value. So the limits of confidence interval can never be a decimal value. Hence the nearest integer value will be 132 and 279. Therefore, the confidence interval of the number of friends will be
Want to see more full solutions like this?
Chapter 7 Solutions
LaunchPad for Moore's Introduction to the Practice of Statistics (12 month access)
- An article in Business Week discussed the large spread between the federal funds rate and the average credit card rate. The table below is a frequency distribution of the credit card rate charged by the top 100 issuers. Credit Card Rates Credit Card Rate Frequency 18% -23% 19 17% -17.9% 16 16% -16.9% 31 15% -15.9% 26 14% -14.9% Copy Data 8 Step 1 of 2: Calculate the average credit card rate charged by the top 100 issuers based on the frequency distribution. Round your answer to two decimal places.arrow_forwardPlease could you check my answersarrow_forwardLet Y₁, Y2,, Yy be random variables from an Exponential distribution with unknown mean 0. Let Ô be the maximum likelihood estimates for 0. The probability density function of y; is given by P(Yi; 0) = 0, yi≥ 0. The maximum likelihood estimate is given as follows: Select one: = n Σ19 1 Σ19 n-1 Σ19: n² Σ1arrow_forward
- Please could you help me answer parts d and e. Thanksarrow_forwardWhen fitting the model E[Y] = Bo+B1x1,i + B2x2; to a set of n = 25 observations, the following results were obtained using the general linear model notation: and 25 219 10232 551 XTX = 219 10232 3055 133899 133899 6725688, XTY 7361 337051 (XX)-- 0.1132 -0.0044 -0.00008 -0.0044 0.0027 -0.00004 -0.00008 -0.00004 0.00000129, Construct a multiple linear regression model Yin terms of the explanatory variables 1,i, x2,i- a) What is the value of the least squares estimate of the regression coefficient for 1,+? Give your answer correct to 3 decimal places. B1 b) Given that SSR = 5550, and SST=5784. Calculate the value of the MSg correct to 2 decimal places. c) What is the F statistics for this model correct to 2 decimal places?arrow_forwardCalculate the sample mean and sample variance for the following frequency distribution of heart rates for a sample of American adults. If necessary, round to one more decimal place than the largest number of decimal places given in the data. Heart Rates in Beats per Minute Class Frequency 51-58 5 59-66 8 67-74 9 75-82 7 83-90 8arrow_forward
- can someone solvearrow_forwardQUAT6221wA1 Accessibility Mode Immersiv Q.1.2 Match the definition in column X with the correct term in column Y. Two marks will be awarded for each correct answer. (20) COLUMN X Q.1.2.1 COLUMN Y Condenses sample data into a few summary A. Statistics measures Q.1.2.2 The collection of all possible observations that exist for the random variable under study. B. Descriptive statistics Q.1.2.3 Describes a characteristic of a sample. C. Ordinal-scaled data Q.1.2.4 The actual values or outcomes are recorded on a random variable. D. Inferential statistics 0.1.2.5 Categorical data, where the categories have an implied ranking. E. Data Q.1.2.6 A set of mathematically based tools & techniques that transform raw data into F. Statistical modelling information to support effective decision- making. 45 Q Search 28 # 00 8 LO 1 f F10 Prise 11+arrow_forwardStudents - Term 1 - Def X W QUAT6221wA1.docx X C Chat - Learn with Chegg | Cheg X | + w:/r/sites/TertiaryStudents/_layouts/15/Doc.aspx?sourcedoc=%7B2759DFAB-EA5E-4526-9991-9087A973B894% QUAT6221wA1 Accessibility Mode பg Immer The following table indicates the unit prices (in Rands) and quantities of three consumer products to be held in a supermarket warehouse in Lenasia over the time period from April to July 2025. APRIL 2025 JULY 2025 PRODUCT Unit Price (po) Quantity (q0)) Unit Price (p₁) Quantity (q1) Mineral Water R23.70 403 R25.70 423 H&S Shampoo R77.00 922 R79.40 899 Toilet Paper R106.50 725 R104.70 730 The Independent Institute of Education (Pty) Ltd 2025 Q Search L W f Page 7 of 9arrow_forward
- COM WIth Chegg Cheg x + w:/r/sites/TertiaryStudents/_layouts/15/Doc.aspx?sourcedoc=%7B2759DFAB-EA5E-4526-9991-9087A973B894%. QUAT6221wA1 Accessibility Mode Immersi The following table indicates the unit prices (in Rands) and quantities of three meals sold every year by a small restaurant over the years 2023 and 2025. 2023 2025 MEAL Unit Price (po) Quantity (q0)) Unit Price (P₁) Quantity (q₁) Lasagne R125 1055 R145 1125 Pizza R110 2115 R130 2195 Pasta R95 1950 R120 2250 Q.2.1 Using 2023 as the base year, compute the individual price relatives in 2025 for (10) lasagne and pasta. Interpret each of your answers. 0.2.2 Using 2023 as the base year, compute the Laspeyres price index for all of the meals (8) for 2025. Interpret your answer. Q.2.3 Using 2023 as the base year, compute the Paasche price index for all of the meals (7) for 2025. Interpret your answer. Q Search L O W Larrow_forwardQUAI6221wA1.docx X + int.com/:w:/r/sites/TertiaryStudents/_layouts/15/Doc.aspx?sourcedoc=%7B2759DFAB-EA5E-4526-9991-9087A973B894%7 26 QUAT6221wA1 Q.1.1.8 One advantage of primary data is that: (1) It is low quality (2) It is irrelevant to the purpose at hand (3) It is time-consuming to collect (4) None of the other options Accessibility Mode Immersive R Q.1.1.9 A sample of fifteen apples is selected from an orchard. We would refer to one of these apples as: (2) ھا (1) A parameter (2) A descriptive statistic (3) A statistical model A sampling unit Q.1.1.10 Categorical data, where the categories do not have implied ranking, is referred to as: (2) Search D (2) 1+ PrtSc Insert Delete F8 F10 F11 F12 Backspace 10 ENG USarrow_forwardepoint.com/:w:/r/sites/TertiaryStudents/_layouts/15/Doc.aspx?sourcedoc=%7B2759DFAB-EA5E-4526-9991-9087A 23;24; 25 R QUAT6221WA1 Accessibility Mode DE 2025 Q.1.1.4 Data obtained from outside an organisation is referred to as: (2) 45 (1) Outside data (2) External data (3) Primary data (4) Secondary data Q.1.1.5 Amongst other disadvantages, which type of data may not be problem-specific and/or may be out of date? W (2) E (1) Ordinal scaled data (2) Ratio scaled data (3) Quantitative, continuous data (4) None of the other options Search F8 F10 PrtSc Insert F11 F12 0 + /1 Backspaarrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill

