Chapter 7, Problem 7.1P

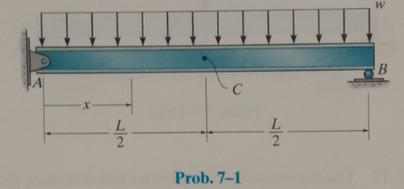
Determine the equation of the elastic curve using the coordinate x, and specify the slope at point A and the deflection at point C. EI is constant.

To determine

The equation of elastic curve using the coordinate $x$ and to specify the slope at point A and the deflection at point C.

Answer to Problem 7.1P

The equation of elastic curve is shown below.

$EI\frac{dv}{dx}=\frac{wL}{2}\times \frac{x^2}{2}-\frac{w}{2}\times \frac{x^3}{3}-\frac{w{L}^3}{24}$

$EIv=\frac{wL}{4}\times \frac{x^3}{3}-\frac{w}{6}\times \frac{x^4}{4}-\frac{w{L}^3}{24}x$

The slope at point A is, $-\frac{w{L}^3}{24EI}$.

The deflection at C is, $-\frac{5w{L}^4}{384EI}$.

Explanation of Solution

Calculation:

The following figure shows the free body diagram of the beam.

Figure-(1)

Write the Equilibrium Equation for the sum of horizontal forces.

$\begin{array}{c}\Sigma F_x=0\\ A_x=0\end{array}$

Here, horizontal reaction at A is $A_x$.

Write the Equilibrium Equation for the sum of vertical forces.

$\begin{array}{l}\Sigma F_y=0\\ A_y+B_y-wL=0\end{array}$

Here, vertical reactions at point A and B are $A_y$ and $B_y$.

Due to symmetry of the beam, the reactions at point A and B will be half of the total load acting on the beam.

$\begin{array}{c}{A}_y=\frac{wL}{2}\\ B_y=\frac{wL}{2}\end{array}$

Consider the section x-x at distance $x$ from point A as shown below.

Write the Equation for sum of moment about x-x.

$\begin{array}{l}\Sigma M_x=0\\ M-\frac{wL}{2}x+wx\frac{x}{2}=0\\ M=\frac{wL}{2}x-wx\frac{x}{2}\end{array}$ ...... (I).

Write the differential equation of the elastic curve as shown below.

$EI\frac{d^{2}v}{d{x}^2}=M$ ...... (II)

Substitute $\frac{wL}{2}x-wx\frac{x}{2}$ for M in Equation (II) and integrate it twice with respect to the $x$.

$EI\frac{dv}{dx}=\frac{wL}{2}\times \frac{x^2}{2}-\frac{w}{2}\times \frac{x^3}{3}+C_1$ ...... (III).

$EIv=\frac{wL}{4}\times \frac{x^3}{3}-\frac{w}{6}\times \frac{x^4}{4}+C_{1}x+C_2$ ...... (IV).

Here, $C_1$ and $C_2$ are the constant.

Calculate the value of $C_2$.

Apply the boundary conditions at the support points.

At $x=0$ and $v=0$.

Substitute $0$ for $x$ and $v$ in equation (IV).

$\begin{array}{c}EI\left(0\right)=\frac{wL}{4}\times \frac{{\left(0\right)}^3}{3}-\frac{w}{6}\times \frac{{\left(0\right)}^4}{4}+C_1\left(0\right)+C_2\\ C_2=0\end{array}$

Calculate the value of $C_1$.

At $x=L$ and $v=0$.

Substitute $L$ for $x$ and $0$ for $C_2$ and $v$ in equation (IV).

$\begin{array}{c}EI\left(0\right)=\frac{wL}{4}\times \frac{{\left(L\right)}^3}{3}-\frac{w}{6}\times \frac{{\left(L\right)}^4}{4}+C_1\left(L\right)+0\\ C_1=-\frac{w{L}^3}{24}\end{array}$

Calculate the slope equation.

Substitute $-\frac{w{L}^3}{24}$ for $C_1$, $\theta$ for $\frac{dv}{dx}$ in equation (III).

$\theta =\frac{1}{EI}\left(\frac{wL}{2}\times \frac{x^2}{2}-\frac{w}{2}\times \frac{x^3}{3}-\frac{w{L}^3}{24}\right)$

   $$ ...... (V)

Calculate the deflection equation.

Substitute $0$ for $C_2$ and $-\frac{w{L}^3}{24}$ for $C_1$ in Equation (IV).

$v=\frac{1}{EI}\left(\frac{wL}{4}\times \frac{x^3}{3}-\frac{w}{6}\times \frac{x^4}{4}-\frac{w{L}^3}{24}x\right)$ ...... (VI).

Calculate the slope at A.

Substitute $0$ for $x$ in Equation (V).

$\begin{array}{c}{\theta }_A=\frac{1}{EI}\left(\frac{wL}{2}\times \frac{{\left(0\right)}^2}{2}-\frac{w}{2}\times \frac{{\left(0\right)}^3}{3}-\frac{w{L}^3}{24}\right)\\ =-\frac{w{L}^3}{24EI}\end{array}$

Calculate the deflection at C.

Substitute $\frac{L}{2}$ for $x$ in Equation (VI).

$\begin{array}{c}{v}_C=\frac{1}{EI}\left(\frac{wL}{4}\times \frac{{\left(\frac{L}{2}\right)}^3}{3}-\frac{w}{6}\times \frac{{\left(\frac{L}{2}\right)}^4}{4}-\frac{w{L}^3}{24}\times \frac{L}{2}\right)\\ =-\frac{5w{L}^4}{384EI}\end{array}$

Conclusion:

The equation of elastic curve is shown below.

$EI\frac{dv}{dx}=\frac{wL}{2}\times \frac{x^2}{2}-\frac{w}{2}\times \frac{x^3}{3}-\frac{w{L}^3}{24}$

$EIv=\frac{wL}{4}\times \frac{x^3}{3}-\frac{w}{6}\times \frac{x^4}{4}-\frac{w{L}^3}{24}x$

The slope at point A is, $-\frac{w{L}^3}{24EI}$.

The deflection at C is, $-\frac{5w{L}^4}{384EI}$.