
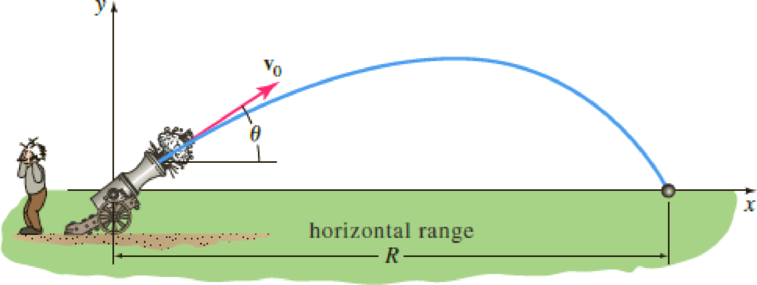
Range of a Projectile—No Air Resistance (a) A projectile, such as the canon ball shown in Figure 7.R.13, has weight w = mg and initial velocity v0 that is tangent to its path of motion. If air resistance and all other forces except its weight are ignored, we saw in Problem 23 of Exercises 4.9 that motion of the projectile is described by the system of linear differential equations
Use the Laplace transform to solve this system subject to the initial conditions
where v0 = |v0| is constant and θ is the constant angle of elevation shown in Figure 7.R.13 on page 330. The solutions x(t) and y(t) are parametric equations of the trajectory of the projectile.
- (b) Use x(t) in part (a) to eliminate the parameter t in y(t). Use the resulting equation for y to show that the horizontal range R of the projectile is given by
- (c) From the formula in part (b), we see that R is a maximum when sin 2θ = 1 or when θ = π/4. Show that the same range—less than the maximum—can be attained by firing the gun at either of two complementary angles θ and π/2 − θ. The only difference is that the smaller angle results in a low trajectory whereas the larger angle gives a high trajectory.
- (d) Suppose g = 32 ft/s2, θ = 38°, and v0 = 300 ft/s. Use part (b) to find the horizontal range of the projectile. Find the time when the projectile hits the ground.
- (e) Use the parametric equations x(t) and y(t) in part (a) along with the numerical data in part (d) to plot the ballistic curve of the projectile. Repeat with θ = 52° and v0 = 300 ft/s. Superimpose both curves on the same
coordinate system .
FIGURE 7.R.13 Projectile in Problem 51
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Student Solutions Manual For Zill's A First Course In Differential Equations With Modeling Applications, 11th
- Solve the equation. Write the smaller answer first. 2 (x-6)² = 36 x = Α x = Previous Page Next Pagearrow_forwardWrite a quadratic equation in factored form that has solutions of x = 2 and x = = -3/5 ○ a) (x-2)(5x + 3) = 0 ○ b) (x + 2)(3x-5) = 0 O c) (x + 2)(5x -3) = 0 ○ d) (x-2)(3x + 5) = 0arrow_forwardA vacant lot is being converted into a community garden. The garden and a walkway around its perimeter have an area of 690 square feet. Find the width of the walkway (x) if the garden measures 14 feet wide by 18 feet long. Write answer to 2 decimal places. (Write the number without units). Hint: add 2x to each of the garden dimensions of 14 x 18 feet to get the total area for the length multiplied by width.arrow_forward
- Solve the rational equation 14 1 + x-6 x x-7 x-7 ○ a) x = 1, x = 8 ○ b) x = 1 ○ c) x = 7 ○ d) x = 1, x = 7arrow_forwardSolve the absolute inequality | x + 5 > 3 ○ a) (-∞, -8] U[-2, ∞0) ☐ b) (-8, -2) c) (-2, ∞0) ○ d) (-∞, - 8) U(-2, ∞0)arrow_forward1) Listen Describe the error in the problem X 3 X x 3 - 2 = 25x = 0 25x 25 x = ±5arrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





