The Cosmic Perspective (9th Edition)
9th Edition
ISBN: 9780134874364
Author: Jeffrey O. Bennett, Megan O. Donahue, Nicholas Schneider, Mark Voit
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7, Problem 2VSC
Use the following questions to check your understanding of some of the many types of visual information used in astronomy. For additional practice, try the Chapter 7 Visual Quiz at Mastering Astronomy.
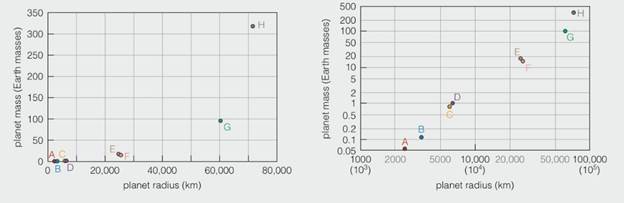
The plots above show the masses of the eight major planets on the vertical axis and their radial on the horizontal axis. The plot on the left shows the information on a linear scale, meaning that each tick mark indicates an increase by the same amount. The plot on the right shows the same information plotted on an exponential scale, meaning that each tick mark represents another actor-of-ten increase. Before proceeding, convince yourself that the points on each plot are the same.
2. Notice how the eight planets group roughly into pairs on the graphs. Which planets are in each pair?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Use Kepler's 3rd Law and the small angle approximation.
a) An object is located in the solar system at a distance from the Sun equal to 41 AU's . What is the objects orbital period?
b) An object seen in a telescope has an angular diameter equivalent to 41 (in units of arc seconds). What is its linear diameter if the object is 250 million km from you? Draw a labeled diagram of this situation.
The table below presents the semi-major axis (a) and Actual orbital period for all of the major planets in the solar system. Cube for each planet the semi-major axis in Astronomical Units. Then take the square root of this number to get the Calculated orbital period of each planet. Fill in the final row of data for each planet.
Table of Data for Kepler’s Third Law:
Table of Data for Kepler’s Third Law:
Planet aau = Semi-Major Axis (AU) Actual Planet Calculated Planet
Period (Yr) Period (Yr)
__________ ______________________ ___________ ________________
Mercury 0.39 0.24
Venus 0.72 0.62
Earth 1.00 1.00
Mars 1.52 1.88
Jupiter…
We need to create a scale model of the solar system (by shrinking the sun down to the size of a basketball or ~30cm). First, we will need to scale down actual solar system dimensions (planet diameters and average orbital radiuses) by converting our units. There are two blank spaces in the table below. We will effectively fill in the missing data in the next set of questions. Use the example below to help you.
Example: What is the scaled diameter of Mercury if the Sun is scaled to the size of a basketball (30 cm)?
The actual diameter of Mercury is 4879 km
The Sun's diameter is 1392000 km
If the Sun is to be reduced to the size of a basketball, then the conversion we need for this equation will be:
30cm1392000km
Here is how we run the conversion: 4879km×30cm1392000km=0.105cm or 0.11cm if we were to round our answer.
This means that if the sun in our model is the size of a basketball, Mercury is the size of a grain of sand. We can also see by looking at the table, that we would…
Chapter 7 Solutions
The Cosmic Perspective (9th Edition)
Ch. 7 - Prob. 1VSCCh. 7 - Use the following questions to check your...Ch. 7 - Use the following questions to check your...Ch. 7 - Use the following questions to check your...Ch. 7 - What do we mean by comparative planetology? Does...Ch. 7 - What would the solar system look like to your...Ch. 7 - Briefly describe the overall layout of the solar...Ch. 7 - For each of the objects in the solar system tour...Ch. 7 - Briefly describe the patterns of motion that we...Ch. 7 - What are the basic differences between the...
Ch. 7 -
7. What do we mean by hydrogen compounds? In...Ch. 7 -
8. What are asteroids? What are comets? Describe...Ch. 7 - What kind of object in Pluto? Explain.Ch. 7 - What is the Kuiper belt? What is the Oort cloud?...Ch. 7 - Describe at least two “exceptions to the rules”...Ch. 7 - Describe and distinguish between space missions...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Does it Make Sense? Decide whether the statement...Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Choose the best answer to each of the following....Ch. 7 - Why Wait? To explore a planet, we often send first...Ch. 7 - Prob. 35EAPCh. 7 - Prob. 37EAPCh. 7 - Patterns of Motion. In one or two paragraphs,...Ch. 7 - Solar System Trends. Answer the following based on...Ch. 7 - Comparing Planetary Conditions. Use both Table 7.1...Ch. 7 - Prob. 41EAPCh. 7 - Size Comparisons. How many Earths could fit inside...Ch. 7 - Asteroid Orbit. Ceres, the largest asteroid, has...Ch. 7 - Density Classification. Calculate the density of a...Ch. 7 - Comparative Weight. Suppose you weigh 100 pounds....Ch. 7 - New Horizons Speed. On its trajectory to Pluto,...Ch. 7 - Planetary Parallax. Suppose observers at Earth’s...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The diagram below shows the orbit of a star with an exoplanet and the corresponding radial velocity curve for the star. Four locations in the planet's orbit are shown. Questions 5-8 refer to this diagram. 5. For each of the four locations of the planet, mark and label on the star's orbit where the star would be at that time. 6. For each of the four positions of the star, draw arrow to indicate which way the star is moving at that time. 7. For each of the four positions of the star, indicate whether the star's light is redshifted, blueshifted, or not shifted. 8. Mark and label the positions on the radial velocity curve that correspond to the four letters. Remember that positive radial velocities correspond to the star moving away from the Earth!! ↑ To Earth Orbit of Star Orbit of Planet D 2 Radial Velocity (m/s) 50 25 -25 -50 ←++ Timearrow_forwardPlease answer parts C and Darrow_forwardDirection: Use your knowledge about solving equations to work out to complete the table below. Show your solution with proper units. R° (meters) T R° / T° { (meters) / Planet Average Times of Radius of Revolution (seconds) (seconds) } Planet's Orbit (Planet's year) R T (seconds) (meters) Mercury 5.7869 x 10:0 7.605 x 10 Venus 1.081 x 101 1.941 x 107 Earth 1.4996 x 10" 3.156 x 10 Mars 2.280 x 101 5.936 x 10 Jupiter 7.783 x 10" 3.743 x 10 Saturn 1.426 x 10 9.296 x 10arrow_forward
- Explain what is meant by the distance ladder in astronomy. Describe briefly how each “rung” of the distance ladder is calibrated so that a reliable measure of distance can be obtained using each of the methods. State clearly the range of distances that can be measured by each method that makes up the distance ladder.arrow_forwardThis is Pre-Calc! Please help and Thank you! Please click the pics for the background info Directions: Answer questions 1-8 based on the information on Table 1. Round all answers to the nearest thousandth and label with the appropriate units. 1. According to Table 1, what is the closest distance between Earth and Mars? 2. According to Table 1, what is the farthest distance between Earth and Mars? 3. Based on your answers from #2 and #3, what is the average distance between the two planets? 4. Based on your answers from #2 and #3, what is the amplitude of the distances? 5. The distance has a period of 772 days. Write a sinusoidal equation relating the number of days and distance from Earth to Mars. 6. Based on the equation from #5, what is the distance between our planets on Mr. Schutt’s birthday (day 187)? 7. Write a sinusoidal equation relating the number of days and the one-waycommunication between Earth to Mars. 8. What is the one-way communication time delay between our planets on…arrow_forwardYou are given the following data from observations of an exoplanet: Using Kepler’s Third Law (r3 = MT2 where M is the mass of the central star) find the orbital radius in astronomical units of this planet. M = 1.5 times the mass of the sun. Remember to convert days to years using 365.25 as the length of a year in days. What is the semimajor axis of this planet in AU? - Knowing the orbital radius in both kn and AU, use the value in km to find the circumference of the orbit, then convert that to meters. (Assume the orbit is a perfect circle). - Knowing the orbital circumference and the period in days, convert the days to seconds (multiply by 86,400) and find the orbital velocity in m/s - With that orbital velocity, the radius of the orbit in meters, find the centripetal acceleration of our exoplanet - Knowing the acceleration that our planet experiences, calculate the force that the host star exerts on the planet - Knowing the force on the planet, the orbital radius, and the mass of the…arrow_forward
- Activity 1: Drawing or Illustration Draw or illustrate Kepler's Three Laws of Motion. Label and explain each illustration. Include the equation used to describe Kepler's Laws of Planetary Motion. Kepler's First Law of Planetary Kepler's Second Law of Motion: Planetary Motion: Drawing/ Illustration Drawing/Illustration Equation: Explanation: Equation: Explanation: Kepler's Third Law of Planetary Motion: Drawing/ Illustration Equation: Explanation: Activity 3: Problem Solving Activity Answer the following problems and show your process using the four guide steps for solving problems. a. The mean solar distance of Earth is 1.50 x m with a period of 1 year. What is the distance of mars from the sun if it has a period of 1.88 years? - b. Titan, the largest moon of Saturn, has a mean orbital radius of 1.22x109 m. The orbital period of Titan is 15.95 days. Hyperion, another moon of Saturn, orbits at a mean radius of 1.48x109 m. Use Kepler's third law of planetary motion to predict the orbital…arrow_forwardIn Table 2, there is a list of 15 planets, some of which are real objects discovered by the Kepler space telescope, and some are hypothetical planets. For each one, you are provided the temperature of the star that each planet orbits in degrees Kelvin (K), the distance that each planet orbits from their star in astronomical units (AUs) and the size or radius of each planet in Earth radii (RE). Since we are concerned with finding Earth-like planets, we will assume that the composition of these planets are similar to Earth's, so we will not directly look at their masses, rather their sizes (radii) along with the other characteristics. Determine which of these 15 planets meets our criteria of a planet that could possibly support Earth-like life. Use the Habitable Planet Classification Flow Chart (below) to complete Table 2. Whenever the individual value you are looking at falls within the range of values specified on the flow chart, mark the cell to the right of the value with a Y for…arrow_forwardbetween a planet and its moon. Procedure/Analysis: Go to: https://www.physicsclassroom.com/Physics-Interactives/Circular-and-Satellite- Motion/Gravitational-Fields/Gravitational-Fields-Interactive Use the program to answer the following questions. 1. A planet and its moon are shown in the simulation window. Click and drag the moon to various positions about the planet and observe the gravitational force vector. In the diagram below, draw a force vector (arrow with arrowhead) to depict the direction and relative magnitude of the force acting upon the moon at the designated locations. Note: the size of the arrow should be representative of the strength of the force.arrow_forward
- Using high resolution adaptive optical techniques, observations of a nearby (9.5 pc) cool star of mass 0.2 solar masses indicate the presence of a small rocky exoplanet in a circular orbit with a radius of 0.01 arcseconds. Using Kepler's Laws, estimate the period of the exoplanet's orbit in days. select units Aarrow_forwardAs discussed in class, the moon is receding from the Earth due to tides at a rate of ~4 cm/year. Let’s assume that rate has been constant throughout time (it wasn’t, but we can use it to illustrate some key points). Its current semi-major axis is 384,400 km.a) If the moon formed 4.5 billion years ago and has been receding from the Earth ever since, what was its original semi-major axis? What was its original orbital period?b) What would the apparent size of the Moon have been in the sky as viewed from Earth? That is, in Hmwk 2, you were told the diameter of the Moon spans about 0.5o when viewed from Earth today. What would it have been when the Moon first formed? Reletive Numbers Relevant Numbers1 AU = 150,000,000 km = 1.5x108 kmEccentricity of Earth’s Orbit: 0.0167Radius of Earth: 6371 kmMass of Earth: 5.96x1024 kgRadius of the Moon: 1737 kmMass of Moon: 7.34x1022 kgRadius of Mars: 3390 kmMass of Mars: 6.4x1023 kgRadius of the Sun: R⦿=696,300 kmMass of the Sun: M⦿=2x1030…arrow_forwardHow can sciences be integrated in designing a water arc? Elaborate in complete sentences. i want a lot of reasons not only 1 reason like gravity or physics i want you to provide me with more reasons please and as it said Elaborate in complete sentencesarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Stars and GalaxiesPhysicsISBN:9781305120785Author:Michael A. Seeds, Dana BackmanPublisher:Cengage Learning
AstronomyPhysicsISBN:9781938168284Author:Andrew Fraknoi; David Morrison; Sidney C. WolffPublisher:OpenStax
Stars and Galaxies
Physics
ISBN:9781305120785
Author:Michael A. Seeds, Dana Backman
Publisher:Cengage Learning
Astronomy
Physics
ISBN:9781938168284
Author:Andrew Fraknoi; David Morrison; Sidney C. Wolff
Publisher:OpenStax
Kepler's Three Laws Explained; Author: PhysicsHigh;https://www.youtube.com/watch?v=kyR6EO_RMKE;License: Standard YouTube License, CC-BY