Excursions in Modern Mathematics, Books a la carte edition (9th Edition)
9th Edition
ISBN: 9780134469041
Author: Peter Tannenbaum
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7, Problem 28E
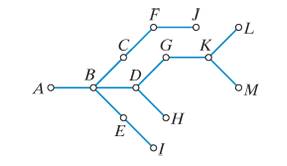
Consider the network shown in
a. Find a spanning tree of the network.
b. Calculate the redundancy of the network.
c. What is the diameter of the network?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
29
Suppose that a mound-shaped data set has a
must mean of 10 and standard deviation of 2.
a. About what percentage of the data should
lie between 6 and 12?
b. About what percentage of the data should
lie between 4 and 6?
c. About what percentage of the data should
lie below 4?
91002 175/1
3
2,3,
ample
and
rical
t?
the
28 Suppose that a mound-shaped data set has a
mean of 10 and standard deviation of 2.
a. About what percentage of the data should
lie between 8 and 12?
b. About what percentage of the data should
lie above 10?
c. About what percentage of the data should
lie above 12?
27 Suppose that you have a data set of 1, 2, 2, 3,
3, 3, 4, 4, 5, and you assume that this sample
represents a population. The mean is 3 and g
the standard deviation is 1.225.10
a. Explain why you can apply the empirical
rule to this data set.
b. Where would "most of the values" in the
population fall, based on this data set?
Chapter 7 Solutions
Excursions in Modern Mathematics, Books a la carte edition (9th Edition)
Ch. 7 - A computer lab has seven computers labeled A...Ch. 7 - The following is a list of the electrical power...Ch. 7 - Consider the network shown in Fig.720_. a. How...Ch. 7 - Consider the network shown in Fig.721_. a. How...Ch. 7 - Consider once again the network shown in. Fig720_....Ch. 7 - Consider once again the network shown in. Fig721_....Ch. 7 - Consider the network shown in. Fig722. This is the...Ch. 7 - Consider the network shown in. Fig723_. This is...Ch. 7 - Consider the tree shown in. Fig724_. a. How many...Ch. 7 - Consider the tree shown in. Fig725. a. How many...
Ch. 7 - In Exercises 11 through 24 you are given...Ch. 7 - Prob. 12ECh. 7 - Prob. 13ECh. 7 - Prob. 14ECh. 7 - In Exercises 11 through 24 you are given...Ch. 7 - Prob. 16ECh. 7 - Prob. 17ECh. 7 - Prob. 18ECh. 7 - Prob. 19ECh. 7 - In Exercises 11 through 24 you are given...Ch. 7 - Prob. 21ECh. 7 - Prob. 22ECh. 7 - Prob. 23ECh. 7 - Prob. 24ECh. 7 - Prob. 25ECh. 7 - Consider the network shown in Fig.727_. a. Find a...Ch. 7 - Prob. 27ECh. 7 - Consider the network shown in Fig.729_. a. Find a...Ch. 7 - Prob. 29ECh. 7 - Prob. 30ECh. 7 - Prob. 31ECh. 7 - Prob. 32ECh. 7 - Prob. 33ECh. 7 - Prob. 34ECh. 7 - Prob. 35ECh. 7 - The 4 by 5 grid shown in Fig. 7-37 represents a...Ch. 7 - Prob. 37ECh. 7 - Find the MST of the network shown in Fig. 7-39...Ch. 7 - Find the MST of the network shown in Fig. 7-40...Ch. 7 - Find the MST of the network shown in Fig. 7-41...Ch. 7 - Prob. 41ECh. 7 - Find the MaxST of the network shown in Fig. 7-39...Ch. 7 - Find the MaxST of the network shown in Fig. 7-40...Ch. 7 - Prob. 44ECh. 7 - The mileage chart in Fig. 742 shows the distances...Ch. 7 - Figure 7-43a shows a network of roads connecting...Ch. 7 - Prob. 47ECh. 7 - Prob. 48ECh. 7 - Prob. 49ECh. 7 - This exercise refers to weighted networks where...Ch. 7 - Prob. 51ECh. 7 - Prob. 52ECh. 7 - Prob. 53ECh. 7 - Prob. 54ECh. 7 - Prob. 55ECh. 7 - Prob. 56ECh. 7 - A bipartite graph is a graph with the property...Ch. 7 - Prob. 58ECh. 7 - Prob. 59E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 30 Explain how you can use the empirical rule to find out whether a data set is mound- shaped, using only the values of the data themselves (no histogram available).arrow_forward5. Let X be a positive random variable with finite variance, and let A = (0, 1). Prove that P(X AEX) 2 (1-A)² (EX)² EX2arrow_forward6. Let, for p = (0, 1), and xe R. X be a random variable defined as follows: P(X=-x) = P(X = x)=p. P(X=0)= 1-2p. Show that there is equality in Chebyshev's inequality for X. This means that Chebyshev's inequality, in spite of being rather crude, cannot be improved without additional assumptions.arrow_forward
- 4. Prove that, for any random variable X, the minimum of EIX-al is attained for a = med (X).arrow_forward8. Recall, from Sect. 2.16.4, the likelihood ratio statistic, Ln, which was defined as a product of independent, identically distributed random variables with mean 1 (under the so-called null hypothesis), and the, sometimes more convenient, log-likelihood, log L, which was a sum of independent, identically distributed random variables, which, however, do not have mean log 1 = 0. (a) Verify that the last claim is correct, by proving the more general statement, namely that, if Y is a non-negative random variable with finite mean, then E(log Y) log(EY). (b) Prove that, in fact, there is strict inequality: E(log Y) < log(EY), unless Y is degenerate. (c) Review the proof of Jensen's inequality, Theorem 5.1. Generalize with a glimpse on (b).arrow_forward2. Derive the component transformation equations for tensors shown be- low where [C] = [BA] is the direction cosine matrix from frame A to B. B[T] = [C]^[T][C]T 3. The transport theorem for vectors shows that the time derivative can be constructed from two parts: the first is an explicit frame-dependent change of the vector whereas the second is an active rotational change of the vector. The same holds true for tensors. Starting from the previous result, derive a version of transport theorem for tensors. [C] (^[T])[C] = dt d B dt B [T] + [WB/A]B[T] – TWB/A] (10 pt) (7pt)arrow_forward
- Use the graph of the function y = f (x) to find the value, if possible. f(x) 8 7 6 Q5 y 3 2 1 x -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 -4 -5 -6 -7 -8+ Olim f(z) x-1+ O Limit does not exist.arrow_forward3. Prove that, for any random variable X, the minimum of E(X - a)² is attained for a = EX. Provedarrow_forwardShade the areas givenarrow_forward
- 7. Cantelli's inequality. Let X be a random variable with finite variance, o². (a) Prove that, for x ≥ 0, P(X EX2x)≤ 02 x² +0² 202 P(|X - EX2x)<≤ (b) Find X assuming two values where there is equality. (c) When is Cantelli's inequality better than Chebyshev's inequality? (d) Use Cantelli's inequality to show that med (X) - EX ≤ o√√3; recall, from Proposition 6.1, that an application of Chebyshev's inequality yields the bound o√√2. (e) Generalize Cantelli's inequality to moments of order r 1.arrow_forwardThe college hiking club is having a fundraiser to buy new equipment for fall and winter outings. The club is selling Chinese fortune cookies at a price of $2 per cookie. Each cookie contains a piece of paper with a different number written on it. A random drawing will determine which number is the winner of a dinner for two at a local Chinese restaurant. The dinner is valued at $32. Since fortune cookies are donated to the club, we can ignore the cost of the cookies. The club sold 718 cookies before the drawing. Lisa bought 13 cookies. Lisa's expected earnings can be found by multiplying the value of the dinner by the probability that she will win. What are Lisa's expected earnings? Round your answer to the nearest cent.arrow_forwardThe Honolulu Advertiser stated that in Honolulu there was an average of 659 burglaries per 400,000 households in a given year. In the Kohola Drive neighborhood there are 321 homes. Let r be the number of homes that will be burglarized in a year. Use the formula for Poisson distribution. What is the value of p, the probability of success, to four decimal places?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Algebra - Pythagorean Theorem; Author: yaymath;https://www.youtube.com/watch?v=D_y_owf1WsI;License: Standard YouTube License, CC-BY
The Organic Chemistry Tutor; Author: Pythagorean Theorem Explained!;https://www.youtube.com/watch?v=B0G35RkmwSw;License: Standard Youtube License