
To determine: The bond’s price at different periods
Introduction:
A bond refers to the debt securities issued by the governments or corporations for raising capital. The borrower does not return the face value until maturity. However, the investor receives the coupons every year until the date of maturity.
Bond price or bond value refers to the present value of the future cash inflows of the bond after discounting at the required rate of return.
Answer to Problem 18QP
The price of the bond at different periods is as follows:
| Time to maturity (Years) | Bond X | Bond Y |
| 13 | $1,126.6776 | $883.3285 |
| 12 | $1,120.4378 | $888.5195 |
| 10 | $1,106.5930 | $900.2923 |
| 5 | $1,062.3745 | $939.9184 |
| 1 | $1,014.2477 | $985.9048 |
| 0 | $1,000.0000 | $1,000.0000 |
Explanation of Solution
Given information:
Bond X is selling at a premium. The coupon rate of Bond X is 8.5 percent and its yield to maturity is 7 percent. The bond will mature in 13 years. Bond Y is selling at a discount. The coupon rate of Bond Y is 7 percent and its yield to maturity is 8.5 percent. The bond will mature in 13 years. Both the bonds make semiannual coupon payments. Assume that the face value of bonds is $1,000.
The formula to calculate annual coupon payment:
The formula to calculate the current price of the bond:
Where,
“C” refers to the coupon paid per period
“F” refers to the face value paid at maturity
“r” refers to the yield to maturity
“t” refers to the periods to maturity
Compute the bond price of Bond X at different maturities:
Compute the annual coupon payment of Bond X:
Hence, the annual coupon payment of Bond X is $85.
The bond value or the price of Bond X at present:
The bond pays the coupons semiannually. The annual coupon payment is $85. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $42.50
Secondly, the remaining time to maturity is 13 years. As the coupon payment is semiannual, the semiannual periods to maturity are 26
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.50 percent
Hence, the current price of the bond is $1,126.6776.
The bond value or the price of Bond X after one year:
The bond pays the coupons semiannually. The annual coupon payment is $85. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $42.50
Secondly, the remaining time to maturity is 12 years after one year from now. As the coupon payment is semiannual, the semiannual periods to maturity are 24
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.50 percent
Hence, the price of the bond will be $1,120.4378 after one year.
The bond value or the price of Bond X after 3 years:
The bond pays the coupons semiannually. The annual coupon payment is $85. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $42.50
Secondly, the remaining time to maturity is 10 years after three years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 20
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.50 percent
Hence, the price of the bond will be $1,106.5930 after three years.
The bond value or the price of Bond X after eight years:
The bond pays the coupons semiannually. The annual coupon payment is $85. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $42.50
Secondly, the remaining time to maturity is 5 years after eight years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 10
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.50 percent
Hence, the price of the bond will be $1,062.3745 after eight years.
The bond value or the price of Bond X after twelve years:
The bond pays the coupons semiannually. The annual coupon payment is $85. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $42.50
Secondly, the remaining time to maturity is one year after twelve years from now. As the coupon payment is semiannual, the semiannual periods to maturity are two
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.50 percent
Hence, the price of the bond will be $1,014.2477 after twelve years.
The bond value or the price of Bond X after thirteen years:
The thirteenth year is the year of maturity for Bond X. In this year, the bondholder will receive the bond’s face value. Hence, the price of the bond will be $1,000 after thirteen years.
Compute the bond price of Bond Y at different maturities:
Compute the annual coupon payment of Bond Y:
Hence, the annual coupon payment of Bond Y is $70.
The bond value or the price of Bond Y at present:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is 13 years. As the coupon payment is semiannual, the semiannual periods to maturity are 26
Thirdly, the yield to maturity is 8.5 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.25 percent
Hence, the current price of the bond is $883.3285.
The bond value or the price of Bond Y after one year:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is 12 years after one year from now. As the coupon payment is semiannual, the semiannual periods to maturity are 24
Thirdly, the yield to maturity is 8.5 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.25 percent
Hence, the price of the bond is $888.5195 after one year.
The bond value or the price of Bond Y after three years:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is 10 years after three years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 20
Thirdly, the yield to maturity is 8.5 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.25 percent
Hence, the price of the bond is $900.2923 after three years.
The bond value or the price of Bond Y after eight years:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is 5 years after three years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 10
Thirdly, the yield to maturity is 8.5 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.25 percent
Hence, the price of the bond is $939.9184 after eight years.
The bond value or the price of Bond Y after twelve years:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is one year after twelve years from now. As the coupon payment is semiannual, the semiannual periods to maturity are two
Thirdly, the yield to maturity is 8.5 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.25 percent
Hence, the price of the bond is $985.9048 after twelve years.
The bond value or the price of Bond Y after thirteen years:
The thirteenth year is the year of maturity for Bond Y. In this year, the bondholder will receive the bond’s face value. Hence, the price of the bond will be $1,000 after thirteen years.
Table indicating the bond prices of Bond X and Bond Y at different maturities:
| Time to maturity (Years) | Bond X | Bond Y |
| 13 | $1,126.6776 | $883.3285 |
| 12 | $1,120.4378 | $888.5195 |
| 10 | $1,106.5930 | $900.2923 |
| 5 | $1,062.3745 | $939.9184 |
| 1 | $1,014.2477 | $985.9048 |
| 0 | $1,000.0000 | $1,000.0000 |
Table 1
Graphical representation of the bond prices of Bond X and Bond Y from Table 1:
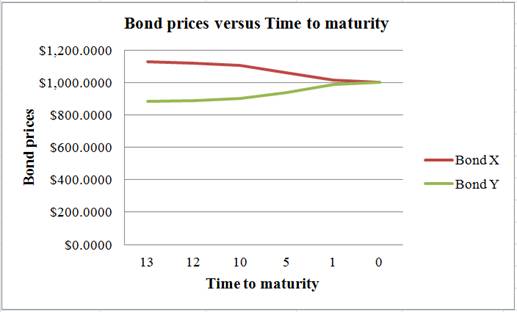
Explanation of the graph:
The graph indicates a “pull to par” effect on the prices of the bonds. The face value of both the bonds is $1,000. Although Bond X is at a premium and Bond Y is at a discount, both the bonds will reach their par values at the time of maturity. The effect of reaching the face value or par value from a discount or premium is known as “pull to par”.
Want to see more full solutions like this?
Chapter 7 Solutions
Fundamentals of Corporate Finance
 Intermediate Financial Management (MindTap Course...FinanceISBN:9781337395083Author:Eugene F. Brigham, Phillip R. DavesPublisher:Cengage Learning
Intermediate Financial Management (MindTap Course...FinanceISBN:9781337395083Author:Eugene F. Brigham, Phillip R. DavesPublisher:Cengage Learning
