
Concept explainers
Derive the system of equations (1) by applying Newton’s second law,
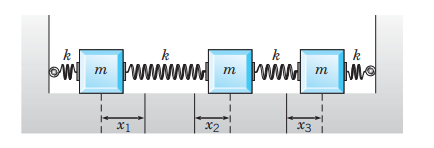
The system of equations describing motions of a three mass and four spring system by applying Newton’s second law
Answer to Problem 1P
Solution:
The system of equations describing motions of a three mass and four spring system are
Explanation of Solution
Given information:
Three masses
Newton’s second law is
The springs follow Hooke’s Law: The force exerted by a spring on a mass is directly proportional to the length of its departure from its equilibrium length.
Explanation:
The first mass’s one side is attached to the wall with the spring and the other side is attached to the second body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the first body is
In the second case, the second body is attached to the first body with the spring and the other side is attached to the third body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the second body is
Similarly, in the third case, the third mass is attached to the wall with the spring and in the other side, it is attached to the second body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the third body is
Thus, the system of equations describing the motions of a three mass and four spring system are
Want to see more full solutions like this?
Chapter 6 Solutions
DIFFERENTIAL EQUATIONS(LL) W/WILEYPLUS
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Thinking Mathematically (6th Edition)
Introductory Statistics
College Algebra with Modeling & Visualization (5th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- 4. Select all of the solutions for x²+x - 12 = 0? A. -12 B. -4 C. -3 D. 3 E 4 F 12 4 of 10arrow_forward2. Select all of the polynomials with the degree of 7. A. h(x) = (4x + 2)³(x − 7)(3x + 1)4 B h(x) = (x + 7)³(2x + 1)^(6x − 5)² ☐ Ch(x)=(3x² + 9)(x + 4)(8x + 2)ª h(x) = (x + 6)²(9x + 2) (x − 3) h(x)=(-x-7)² (x + 8)²(7x + 4)³ Scroll down to see more 2 of 10arrow_forward1. If all of the zeros for a polynomial are included in the graph, which polynomial could the graph represent? 100 -6 -2 0 2 100 200arrow_forward
- 3. Select the polynomial that matches the description given: Zero at 4 with multiplicity 3 Zero at −1 with multiplicity 2 Zero at -10 with multiplicity 1 Zero at 5 with multiplicity 5 ○ A. P(x) = (x − 4)³(x + 1)²(x + 10)(x — 5)³ B - P(x) = (x + 4)³(x − 1)²(x − 10)(x + 5)³ ○ ° P(x) = (1 − 3)'(x + 2)(x + 1)"'" (x — 5)³ 51 P(r) = (x-4)³(x − 1)(x + 10)(x − 5 3 of 10arrow_forwardMatch the equation, graph, and description of transformation. Horizontal translation 1 unit right; vertical translation 1 unit up; vertical shrink of 1/2; reflection across the x axis Horizontal translation 1 unit left; vertical translation 1 unit down; vertical stretch of 2 Horizontal translation 2 units right; reflection across the x-axis Vertical translation 1 unit up; vertical stretch of 2; reflection across the x-axis Reflection across the x - axis; vertical translation 2 units down Horizontal translation 2 units left Horizontal translation 2 units right Vertical translation 1 unit down; vertical shrink of 1/2; reflection across the x-axis Vertical translation 2 units down Horizontal translation 1 unit left; vertical translation 2 units up; vertical stretch of 2; reflection across the x - axis f(x) = - =-½ ½ (x − 1)²+1 f(x) = x²-2 f(x) = -2(x+1)²+2 f(x)=2(x+1)²-1 f(x)=-(x-2)² f(x)=(x-2)² f(x) = f(x) = -2x²+1 f(x) = -x²-2 f(x) = (x+2)²arrow_forwardWhat is the vertex, increasing interval, decreasing interval, domain, range, root/solution/zero, and the end behavior?arrow_forward
- Calculate a (bxc) where a = i, b = j, and c = k.arrow_forwardi+2j+3k = (1,2,3) and b = -i-k. Calculate the cross product a x b where a Next calculate the area of the parallelogram spanned by a and b.arrow_forwardThe measured receptance data around two resonant picks of a structure are tabulated in the followings. Find the natural frequencies, damping ratios, and mode shapes of the structure. (30 points) (@)×10 m/N α₁₂ (@)×10 m/N w/2z (Hz) 99 0.1176 0.17531 0.1114 -0.1751i 101 -0.0302 0.2456i -0.0365 -0.2453i 103 -0.1216 0.1327i -0.1279-0.1324i 220 0.0353 0.0260i -0.0419+0.0259i 224 0.0210 0.0757i |-0.0273 +0.0756i 228 -0.0443 0.0474i 0.0382 +0.0474iarrow_forward
- Q3: Define the linear functional J: H(2) R by 1(v) = a(v. v) - L(v) Let u be the unique weak solution to a(u,v) = L(v) in H() and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under algebraic form u Au-ub. J(u)=u'Au- Where A. b are repictively the stiffence matrix and the load vectorarrow_forward== 1. A separable differential equation can be written in the form hy) = g(a) where h(y) is a function of y only, and g(x) is a function of r only. All of the equations below are separable. Rewrite each of these in the form h(y) = g(x), then find a general solution by integrating both sides. Determine whether the solutions you found are explicit (functions) or implicit (curves but not functions) (a) 1' = — 1/3 (b) y' = = --- Y (c) y = x(1+ y²)arrow_forwardJa дх dx dx Q3: Define the linear functional J: H()-R by تاریخ (v) = ½a(v, v) - (v) == Let u be the unique weak solution to a(u,v) = L(v) in H₁(2) and suppose that a(...) is a symmetric bilinear form on H() prove that a Buy v) = 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under J(u)=u' Au-ub, algebraic form Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer only 1-show that thelation to -Auf in N, u = 0 on a satisfies the stability Vulf and show that V(u-u,)||² = ||vu||2 - ||vu||2 lu-ulls Chu||2 2- Prove that Where =1 ||ul|= a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinear form a(u, v) = (Au, Av) + (Vu, Vv) + (Vu, v) + (u, v) Show that a(u, v) continues and V- elliptic on H(2) (3) (0.0), (3.0)arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
