USING AND UNDERSTANDING MATHEMATICS W/
7th Edition
ISBN: 9780135239919
Author: BENNETT AND BR
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6.A, Problem 37E
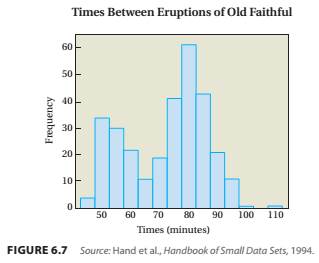
Smooth Distributions. Through each histogram, draw a smooth curve that captures its important features. Then classify the distribution according to its number of peaks, symmetry or skew-ness, and variation.
37. Times between 300 eruptions of Old Faithful geyser in Yellowstone National Park, shown in Figure 6.7
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
To compare two elementary schools regarding teaching of reading skills, 12 sets of identical twins were used. In each case, one child was selected at random and sent to school A, and his or her twin was sent to school B. Near the end of fifth grade, an achievement test was given to each child. The results follow:
Twin Pair
1
2
3
4
5
6
School A
169
157
115
99
119
113
School B
123
157
112
99
121
122
Twin Pair
7
8
9
10
11
12
School A
120
121
124
145
138
117
School B
153
90
124
140
142
102
Suppose a sign test for matched pairs with a 1% level of significance is used to test the hypothesis that the schools have the same effectiveness in teaching reading skills against the alternate hypothesis that the schools have different levels of effectiveness in teaching reading skills. Let p denote portion of positive signs when the scores of school B are subtracted from the corresponding scores of school…
A horse trainer teaches horses to jump by using two methods of instruction. Horses being taught by method A have a lead horse that accompanies each jump. Horses being taught by method B have no lead horse. The table shows the number of training sessions required before each horse performed the jumps properly.
Method A
25
23
39
29
37
20
Method B
41
21
46
42
24
44
Method A
45
35
27
31
34
49
Method B
26
43
47
32
40
Use a rank-sum test with a5% level of significance to test the claim that there is no difference between the training sessions distributions. If the value of the sample test statistic R, the rank-sum, is 150, calculate the P-value. Round your answer to four decimal places.
A data processing company has a training program for new salespeople. After completing the training program, each trainee is ranked by his or her instructor. After a year of sales, the same class of trainees is again ranked by a company supervisor according to net value of the contracts they have acquired for the company. The results for a random sample of 11 salespeople trained in the last year follow, where x is rank in training class and y is rank in sales after 1 year. Lower ranks mean higher standing in class and higher net sales.
Person
1
2
3
4
5
6
x rank
8
11
2
4
5
3
y rank
7
10
1
3
2
4
Person
7
8
9
10
11
x rank
7
9
10
1
6
y rank
8
11
9
6
5
Using a 1% level of significance, test the claim that the relation between x and y is monotone (either increasing or decreasing). Verify that the Spearman rank correlation coefficient . This implies that the P-value lies between 0.002 and 0.01. State…
Chapter 6 Solutions
USING AND UNDERSTANDING MATHEMATICS W/
Ch. 6.A - Prob. 1QQCh. 6.A - On an astronomy exam, 20 students score below 79...Ch. 6.A - One hundred students take a chemistry exam. All...Ch. 6.A - Twenty students take a political science exam....Ch. 6.A - A survey asks students to state many sodas they...Ch. 6.A - Among professional actors, a small number of...Ch. 6.A - The distribution of wages at a company is...Ch. 6.A - Compared to a distribution with a broad central...Ch. 6.A - If you compared the distribution of weights of 20...Ch. 6.A - The mayor of a town is considering a run for...
Ch. 6.A - 1. Define and distinguish among mean, median, and...Ch. 6.A - Prob. 2ECh. 6.A - Briefly describe at least two possible sources of...Ch. 6.A - Prob. 4ECh. 6.A - Prob. 5ECh. 6.A - Prob. 6ECh. 6.A - In my data set of 10 exam scores, the mean turned...Ch. 6.A - In my data set of 10 exam scores, the median...Ch. 6.A - I made a distribution of 15 apartment rents in my...Ch. 6.A - Two extremely tall people skewed the distribution...Ch. 6.A - The distribution of grades was left-skewed, but...Ch. 6.A - There’s much more variation in the ages of the...Ch. 6.A - 13-18: Mean, Median, and Mode. Compute the mean,...Ch. 6.A - Mean, Median, and Mode. Compute the mean, median,...Ch. 6.A - Mean, Median, and Mode. Compute the mean, median,...Ch. 6.A - Mean, Median, and Mode. Compute the mean, median,...Ch. 6.A - 13–18: Mean, Median, and Mode. Compute the mean,...Ch. 6.A - 13-18: Mean, Median, and Mode. Compute the mean,...Ch. 6.A - Outlier Coke. Cans of Coca-Cola vary slightly in...Ch. 6.A - 20. Margin of Victory. The following data give the...Ch. 6.A - Appropriate Average. For each of the following...Ch. 6.A - 21-26: Appropriate Average. For each of the...Ch. 6.A - 21-26: Appropriate Average. For each of the...Ch. 6.A - 21-26: Appropriate Average. For each of the...Ch. 6.A - 21-26: Appropriate Average. For each of the...Ch. 6.A - 21-26: Appropriate Average. For each of the...Ch. 6.A - 27-34: Describing Distributions Consider the...Ch. 6.A - Describing Distributions. Consider the following...Ch. 6.A - 27-34: Describing Distributions Consider the...Ch. 6.A - Describing Distributions. Consider the following...Ch. 6.A - 27-34: Describing Distributions Consider the...Ch. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Prob. 33ECh. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Prob. 35ECh. 6.A - 35-36: Understanding Distributions. For the given...Ch. 6.A - Smooth Distributions. Through each histogram, draw...Ch. 6.A - Smooth Distributions. For each histogram, draw a...Ch. 6.A - Smooth Distributions. For each histogram, draw a...Ch. 6.A - Prob. 40ECh. 6.A - Family Income. Suppose you study family income in...Ch. 6.A - Airline Delays. Suppose you are a scheduler for a...Ch. 6.A - Weighted Means. We often deal with weighted means,...Ch. 6.A - Weighted Means. We often deal with weighted means,...Ch. 6.A - Prob. 45ECh. 6.A - Prob. 46ECh. 6.A - Prob. 47ECh. 6.A - Prob. 48ECh. 6.A - 50. Daily Averages. Cite three examples of...Ch. 6.A - 51. Distributions in the News. Find three recent...Ch. 6.A - Answer the following questions using procedures...Ch. 6.A - Prob. 52ECh. 6.A - 53. StatCrunch Project. Choose a data set...Ch. 6.B - The lowest score on an exam was 62, the median...Ch. 6.B - Which of the following is not part of a...Ch. 6.B - The lower quartile for hourly wages at a coffee...Ch. 6.B - Is it possible for a distribution to have a mean...Ch. 6.B - Suppose you are given the mean and just one data...Ch. 6.B - The standard deviation is best described as a...Ch. 6.B - What type of data distribution has a negative...Ch. 6.B - In any distribution, it is always true that a. the...Ch. 6.B - Which data set would you expect to have the...Ch. 6.B - Professors Smith, Jones, and Garcia all got the...Ch. 6.B - Consider two grocery stores at which the mean time...Ch. 6.B - Describe how we define and calculate the range of...Ch. 6.B - Prob. 3ECh. 6.B - Prob. 4ECh. 6.B - Prob. 5ECh. 6.B - Prob. 6ECh. 6.B - The distributions of scores on two exams had the...Ch. 6.B - The highest exam score was in the upper quartile...Ch. 6.B - For the 30 students who took the test, the high...Ch. 6.B - I examined the data carefully, and the range was...Ch. 6.B - The standard deviation for the heights of a group...Ch. 6.B - The mean gas mileage of the compact cars we tested...Ch. 6.B - 13. Big Bank Verification. Find the mean and...Ch. 6.B - Prob. 14ECh. 6.B - Comparing Variations. Consider the following data...Ch. 6.B - Prob. 16ECh. 6.B - Prob. 17ECh. 6.B - Comparing Variations. Consider the following data...Ch. 6.B - Understanding Variation. The following exercises...Ch. 6.B - Understanding Variation. The following exercises...Ch. 6.B - Pizza Deliveries. After recording the pizza...Ch. 6.B - Airline Arrival Times. Two airlines have data on...Ch. 6.B - 23. Portfolio Standard Deviation. The book...Ch. 6.B - Defect Rates. Two factories each produce 1000...Ch. 6.B - 25. Ice Cream Deviations. Each night you total the...Ch. 6.B - Vet Data. A small animal veterinarian reviews her...Ch. 6.B - Prob. 27ECh. 6.B - Prob. 28ECh. 6.B - 29. Quality Control. An auto transmission...Ch. 6.B - Web Data Sets. Go to any website that gives data...Ch. 6.B - Prob. 31ECh. 6.B - Prob. 32ECh. 6.B - Prob. 33ECh. 6.B - Prob. 34ECh. 6.B - 35. Variation in StatCrunch. Load the data set...Ch. 6.B - 36. StatCrunch Project. Choose a data set...Ch. 6.C - Graphs of normal distributions a. always look...Ch. 6.C - In a normal distribution, the mean a. is equal to...Ch. 6.C - In a normal distribution, data values farther from...Ch. 6.C - Consider wages at a fast food restaurant where...Ch. 6.C - In a normal distribution, about 2/3 Of the data...Ch. 6.C - Suppose a car driven under different conditions...Ch. 6.C - Consider again the car described in Question 6. On...Ch. 6.C - Consider an exam with a normal distribution of...Ch. 6.C - An acquaintance tells you that his IQ is in the...Ch. 6.C - The height of a particular 7-year-old girl has a...Ch. 6.C - 1. What is a normal distribution? Briefly describe...Ch. 6.C - 2. What is the 68-95-99.7 rule for normal...Ch. 6.C - 3. What is a standard score? How do you find the...Ch. 6.C - Prob. 4ECh. 6.C - The heights of male basketball players at Kentucky...Ch. 6.C - The weights of babies born at Belmont Hospital are...Ch. 6.C - The weights of babies born at Belmont Hospital are...Ch. 6.C - On yesterday's mathematics exam, the standard...Ch. 6.C - My professor graded the final on a curve, and she...Ch. 6.C - Jack is the 50th percentile for height, so he is...Ch. 6.C - Prob. 11ECh. 6.C - Prob. 12ECh. 6.C - Prob. 13ECh. 6.C - 13-18: Normal Distributions. State, with an...Ch. 6.C - 13-18: Normal Distributions. State, with an...Ch. 6.C - Normal Distributions. State, with an explanation,...Ch. 6.C - Prob. 17ECh. 6.C - 13-18: Normal Distributions. State, with an...Ch. 6.C - The 68-95-99.7 Rule. A set of test scores is...Ch. 6.C - The 68-95-99.7 Rule. The resting heart rates for a...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - 21-28: Psychology Exam. The scores on a psychology...Ch. 6.C - 21-28: Psychology Exam. The scores on a psychology...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Standard Scores and Percentiles. Use Table 6.3 to...Ch. 6.C - Standard Scores and Percentiles. Use Table 6.3 to...Ch. 6.C - Percentiles. Use Table 6.4 to find the approximate...Ch. 6.C - Percentiles. Use Table 6.4 to find the approximate...Ch. 6.C - Pregnancy Length. Actual lengths of terms are...Ch. 6.C - Pregnancy Length. Actual lengths of terms are...Ch. 6.C - Prob. 35ECh. 6.C - Prob. 36ECh. 6.C - Heights. According to data from the National...Ch. 6.C - Body Mass Index (BMI). The body mass indexes of...Ch. 6.C - 39. Is It Likely? Suppose you read that the...Ch. 6.C - Prob. 40ECh. 6.C - GRE Scores. Scores on the verbal Graduate Record...Ch. 6.C - 41-47: GRE Scores. Scores on the verbal section of...Ch. 6.C - 41-47: GRE Scores. Scores on the verbal section of...Ch. 6.C - Prob. 44ECh. 6.C - 41-47: GRE Scores. Scores on the verbal section of...Ch. 6.C - Prob. 46ECh. 6.C - Prob. 47ECh. 6.C - Normal Distributions. Many data sets described in...Ch. 6.C - Normal Demonstration. Do a Web search on the...Ch. 6.C - Heights of American Men. The heights of American...Ch. 6.C - Normal Distributions in StatCrunch. Go to the work...Ch. 6.C - Prob. 52ECh. 6.D - Prob. 1QQCh. 6.D - Prob. 2QQCh. 6.D - Prob. 3QQCh. 6.D - Prob. 4QQCh. 6.D - A poll finds that 35% of the people surveyed...Ch. 6.D - Prob. 6QQCh. 6.D - Consider a survey with a margin of error of 4%. If...Ch. 6.D - Prob. 8QQCh. 6.D - Prob. 9QQCh. 6.D - Prob. 10QQCh. 6.D - Prob. 1ECh. 6.D - Prob. 2ECh. 6.D - Prob. 3ECh. 6.D - Prob. 4ECh. 6.D - Prob. 5ECh. 6.D - Prob. 6ECh. 6.D - Prob. 7ECh. 6.D - Prob. 8ECh. 6.D - Prob. 9ECh. 6.D - Prob. 10ECh. 6.D - Both agencies conducted their surveys carefully,...Ch. 6.D - If you want to reduce the margin of error in your...Ch. 6.D - Prob. 13ECh. 6.D - Prob. 14ECh. 6.D - Prob. 15ECh. 6.D - Subjective Significance. For each of the following...Ch. 6.D - 15-20: Subjective Significance. For each of the...Ch. 6.D - Prob. 18ECh. 6.D - Prob. 19ECh. 6.D - 15-20: Subjective Significance. For each of the...Ch. 6.D - Human Body Temperature. A study by University of...Ch. 6.D - Seat Belts and Children. In a study of children...Ch. 6.D - SAT Preparation. A study of 75 students who took...Ch. 6.D - Weight by Age. A National Health Survey determined...Ch. 6.D - Margin of Error. Find the margin of error and the...Ch. 6.D - Prob. 26ECh. 6.D - 25-32: Margin of Error. Find the margin of error...Ch. 6.D - Prob. 28ECh. 6.D - Prob. 29ECh. 6.D - 25-32: Margin of Error. Find the margin of error...Ch. 6.D - 25-32: Margin of Error. Find the margin of error...Ch. 6.D - Margin of Error. Find the margin of error and the...Ch. 6.D - 33-38: Formulating Hypotheses. Consider the...Ch. 6.D - Prob. 34ECh. 6.D - Prob. 35ECh. 6.D - Prob. 36ECh. 6.D - Prob. 37ECh. 6.D - Prob. 38ECh. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D - Prob. 44ECh. 6.D - Prob. 45ECh. 6.D - Prob. 46ECh. 6.D - Prob. 47ECh. 6.D - Better Margin of Error. Suppose you want to...Ch. 6.D - Prob. 49ECh. 6.D - Recent Polls. Visit the websites of polling...Ch. 6.D - Prob. 51ECh. 6.D - Statistical Significance. Find a recent news...Ch. 6.D - Prob. 53ECh. 6.D - Hypothesis Testing. Find a news report describing...Ch. 6.D - 55. Confidence Interval. Go to and choose...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Sand and clay studies were conducted at a site in California. Twelve consecutive depths, each about 15 cm deep, were studied and the following percentages of sand in the soil were recorded. 34.4 27.1 30.8 28.0 32.2 27.6 32.8 25.2 31.4 33.5 24.7 28.4 Converting this sequence of numbers to a sequence of symbols A and B, where A indicates a value above the median and B denotes a value below the median gives ABABABABAABB. Test the sequence for randomness about the median with a 5% level of significance. Verify that the number of runs is 10. What is the upper critical value c2? arrow_forwardSand and clay studies were conducted at a site in California. Twelve consecutive depths, each about 15 cm deep, were studied and the following percentages of sand in the soil were recorded. 34.4 27.1 30.8 28.0 32.2 27.6 32.8 25.2 31.4 33.5 24.7 28.4 Converting this sequence of numbers to a sequence of symbols A and B, where A indicates a value above the median and B denotes a value below the median gives ABABABABAABB. Test the sequence for randomness about the median with a 5% level of significance. Verify that the number of runs is 10. What is the upper critical value c2?arrow_forward29% of all college students major in STEM (Science, Technology, Engineering, and Math). If 46 college students are randomly selected, find the probability thata. Exactly 11 of them major in STEM. b. At most 12 of them major in STEM. c. At least 11 of them major in STEM. d. Between 11 and 15 (including 11 and 15) of them major in STEM.arrow_forward
- Sand and clay studies were conducted at a site in California. Twelve consecutive depths, each about 15 cm deep, were studied and the following percentages of sand in the soil were recorded. 27.3 34.6 30.6 27.8 33.4 31.5 27.3 31.2 32.0 24.7 24.4 28.2 Test this sequence for randomness about the median. Converting this sequence of numbers to a sequence of symbols A and B, where A indicates a value above the median and B denotes a value below the median gives BAABAABAABBB. Verify that the number of runs is 7, the lower critical number is 3, and the upper critical number is 11. Use a 5% level of significance. State the conclusion of the test and interpret your results.arrow_forward29% of all college students major in STEM (Science, Technology, Engineering, and Math). If 46 college students are randomly selected, find the probability thata. Exactly 11 of them major in STEM. b. At most 12 of them major in STEM. c. At least 11 of them major in STEM. d. Between 11 and 15 (including 11 and 15) of them major in STEM.arrow_forward4. Assume that a risk-free money market account is added to the market described in Q3. The continuously compounded rate of return on the money market account is log (1.1). (i) For each given μ, use Lagrange multipliers to determine the proportions (as a function of μ) of wealth invested in the three assets available for the minimum variance portfolio with expected return μ. (ii) Determine the market portfolio in this market and calculate its Sharp ratio.arrow_forward
- 3. A market consists of two risky assets with rates of return R₁ and R2 and no risk-free asset. From market data the following have been estimated: ER₁ = 0.25, ER2 = 0.05, Var R₁ = 0.01, Var R2 = 0.04 and the correlation between R1 and R2 is p = -0.75. (i) Given that an investor is targeting a total expected return of μ = 0.2. What portfolio weights should they choose to meet this goal with minimum portfolio variance? Correct all your calculations up to 4 decimal points. (ii) Determine the global minimum-variance portfolio and the expected return and variance of return of this portfolio (4 d.p.). (iii) Sketch the minimum-variance frontier in the μ-σ² plane and indicate the efficient frontier. (iv) Without further calculation, explain how the minimum variance of the investor's portfolio return will change if the two risky assets were independent.arrow_forward2. A landlord is about to write a rental contract for a tenant which lasts T months. The landlord first decides the length T > 0 (need not be an integer) of the contract, the tenant then signs it and pays an initial handling fee of £100 before moving in. The landlord collects the total amount of rent erT at the end of the contract at a continuously compounded rate r> 0, but the contract stipulates that the tenant may leave before T, in which case the landlord only collects the total rent up until the tenant's departure time 7. Assume that 7 is exponentially distributed with rate > 0, λ‡r. (i) Calculate the expected total payment EW the landlord will receive in terms of T. (ii) Assume that the landlord has logarithmic utility U(w) = log(w - 100) and decides that the rental rate r should depend on the contract length T by r(T) = λ √T 1 For each given λ, what T (as a function of X) should the landlord choose so as to maximise their expected utility? Justify your answer. Hint. It might be…arrow_forwardPlease solving problem2 Problem1 We consider a two-period binomial model with the following properties: each period lastsone (1) year and the current stock price is S0 = 4. On each period, the stock price doubleswhen it moves up and is reduced by half when it moves down. The annual interest rateon the money market is 25%. (This model is the same as in Prob. 1 of HW#2).We consider four options on this market: A European call option with maturity T = 2 years and strike price K = 5; A European put option with maturity T = 2 years and strike price K = 5; An American call option with maturity T = 2 years and strike price K = 5; An American put option with maturity T = 2 years and strike price K = 5.(a) Find the price at time 0 of both European options.(b) Find the price at time 0 of both American options. Compare your results with (a)and comment.(c) For each of the American options, describe the optimal exercising strategy.arrow_forward
- Please ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forwardThis question builds on an earlier problem. The randomized numbers may have changed, but have your work for the previous problem available to help with this one. A 4-centimeter rod is attached at one end to a point A rotating counterclockwise on a wheel of radius 2 cm. The other end B is free to move back and forth along a horizontal bar that goes through the center of the wheel. At time t=0 the rod is situated as in the diagram at the left below. The wheel rotates counterclockwise at 1.5 rev/sec. At some point, the rod will be tangent to the circle as shown in the third picture. A B A B at some instant, the piston will be tangent to the circle (a) Express the x and y coordinates of point A as functions of t: x= 2 cos(3πt) and y= 2 sin(3t) (b) Write a formula for the slope of the tangent line to the circle at the point A at time t seconds: -cot(3πt) sin(3лt) (c) Express the x-coordinate of the right end of the rod at point B as a function of t: 2 cos(3πt) +411- 4 -2 sin (3лt) (d)…arrow_forward5. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.AE.003. y y= ex² 0 Video Example x EXAMPLE 3 (a) Use the Midpoint Rule with n = 10 to approximate the integral कर L'ex² dx. (b) Give an upper bound for the error involved in this approximation. SOLUTION 8+2 1 L'ex² d (a) Since a = 0, b = 1, and n = 10, the Midpoint Rule gives the following. (Round your answer to six decimal places.) dx Ax[f(0.05) + f(0.15) + ... + f(0.85) + f(0.95)] 0.1 [0.0025 +0.0225 + + e0.0625 + 0.1225 e0.3025 + e0.4225 + e0.2025 + + e0.5625 €0.7225 +0.9025] The figure illustrates this approximation. (b) Since f(x) = ex², we have f'(x) = 0 ≤ f'(x) = < 6e. ASK YOUR TEACHER and f'(x) = Also, since 0 ≤ x ≤ 1 we have x² ≤ and so Taking K = 6e, a = 0, b = 1, and n = 10 in the error estimate, we see that an upper bound for the error is as follows. (Round your final answer to five decimal places.) 6e(1)3 e 24( = ≈arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License