Chapter 6.6, Problem 113E

(a)

To determine

To calculate:

The cube roots of complex number.

Answer to Problem 113E

The cube roots of complex number are

  $5\left(\cos \frac{4\pi }{9}+i\sin \frac{4\pi }{9}\right),5\left(\cos \frac{10\pi }{9}+i\sin \frac{10\pi }{9}\right)$ and $5\left(\cos \frac{16\pi }{9}+i\sin \frac{16\pi }{9}\right)$

Explanation of Solution

Given information:

Complex number $-\frac{125}{2}\left(1+\sqrt{3}i\right)$

Formula used:

The formula to calculate the roots of complex number are given by,

  $n\sqrt{r}\left(\cos \frac{\theta +2\pi k}{n}+i\sin \frac{\theta +2\pi k}{n}\right)$

Where, $k=0,1,\mathrm{2...},n-1$

Calculation:

Now first to find the cube roots of the complex number $-\frac{125}{2}\left(1+\sqrt{3}i\right)$ by using the above formula,

Now, first the complex number $\left(1+\sqrt{3}i\right)$ is in the first quadrant.

The modulus of the complex number is given by,

  $\begin{array}{l}r=\sqrt{1^2+\sqrt{3^2}}\\ r=2\end{array}$

Now the argument is given by,

  $\begin{array}{l}\theta =\arctan \sqrt{3}\\ \theta =\frac{\pi }{3}\end{array}$

The trigonometric form the angle is now written as,

  $z=2\left(\cos \frac{\pi }{3}+i\sin \frac{\pi }{3}\right)$ ,

Now the complex number is written as,

  $\begin{array}{l}z=-\frac{125}{2}\left[2\left(\cos \frac{\pi }{3}\right)+i\sin \frac{\pi }{3}\right]\\ z=-125\left(\cos \frac{\pi }{3}+i\sin \frac{\pi }{3}\right)\\ z=125\left(\cos \frac{-\pi }{3}+i\sin \frac{-\pi }{3}\right)\end{array}$

Now as the sine and cosine are negative in the third quadrant,

  $z=125\left(\cos \frac{4\pi }{3}+i\sin \frac{4\pi }{3}\right)$

After this, to find the $n^{th}$ root of the complex number put all the values in given formula,

  $n\sqrt{r}\left(\cos \frac{\theta +2\pi k}{n}+i\sin \frac{\theta +2\pi k}{n}\right)$

Now,

  $3\sqrt{125}\left(\cos \frac{\frac{4\pi }{3}+2\pi k}{3}\right)+i\sin \frac{\frac{4\pi }{3}+2\pi k}{3}$

  $=5\left(\cos \frac{4\pi +6\pi k}{9}\right)+i\sin \frac{4\pi +6\pi k}{9}$

Now, find the values for $k=0,1,2$

For $k=0$ ,

  $\begin{array}{l}5\left(\cos \frac{4\pi +6\pi k}{9}\right)+i\sin \frac{4\pi +6\pi k}{9}\\ =5\left(\cos \frac{4\pi }{9}+i\sin \frac{4\pi }{9}\right)\end{array}$

For $k=1$

  $\begin{array}{l}5\left(\cos \frac{4\pi +6\pi \times 1}{9}\right)+i\sin \frac{4\pi +6\pi \times 1}{9}\\ =5\left(\cos \frac{4\pi +6\pi }{9}+i\sin \frac{4\pi +6\pi }{9}\right)\end{array}$

  $=5\left(\cos \frac{10\pi }{9}+i\sin \frac{10\pi }{9}\right)$

Now, for $k=2$

  $\begin{array}{l}5\left(\cos \frac{4\pi +6\pi \times 2}{9}\right)+i\sin \frac{4\pi +6\pi \times 2}{9}\\ =5\left(\cos \frac{4\pi +12\pi }{9}+i\sin \frac{4\pi +12\pi }{9}\right)\\ =5\left(\cos \frac{16\pi }{9}+i\sin \frac{16\pi }{9}\right)\end{array}$

(b)

To determine

To calculate:

And write the roots in standard form

Answer to Problem 113E

The roots in standard form are $0.8682+4.9240i$ , $-4.6985-1.7101$ and $3.8302-3.2140i$

Explanation of Solution

Given information:

The roots of complex number,

  $5\left(\cos \frac{4\pi }{9}+i\sin \frac{4\pi }{9}\right)$ ,

  $5\left(\cos \frac{10\pi }{9}+i\sin \frac{10\pi }{9}\right)$ $,$

  $5\left(\cos \frac{16\pi }{9}+i\sin \frac{16\pi }{9}\right)$

Calculation:

Now write the standard form of all the given roots in trigonometric form.

For,

  $5\left(\cos \frac{4\pi }{9}+i\sin \frac{4\pi }{9}\right)$ ,

The standard form is given as,

  $\begin{array}{l}5\left(\cos \frac{4\pi }{9}+i\sin \frac{4\pi }{9}\right)\\ =5\left(\cos \frac{4\times 180}{9}+i\sin \frac{4\times 180}{9}\right)\\ =5\left(\cos 80+i\sin 80\right)\\ =0.8682+4.9240i\end{array}$

For,

  $5\left(\cos \frac{10\pi }{9}+i\sin \frac{10\pi }{9}\right)$

The standard form is written as,

  $\begin{array}{l}=5\left(\cos \frac{10\times 180}{9}+i\sin \frac{10\times 180}{9}\right)\\ =5\left(\cos \frac{1800}{9}+i\sin \frac{1800}{9}\right)\\ =5\left(\cos 200+i\sin 200\right)\end{array}$

As the sine and cos have the negative value in the third quadrant,

  $\begin{array}{l}=5\left(-\cos 20-i\sin 20\right)\\ =-4.6985-1.7101\end{array}$

Now, the standard form for,

  $\begin{array}{l}5\left(\cos \frac{16\times 180}{9}+i\sin \frac{16\times 180}{9}\right)\\ =5\left(\cos \frac{2880}{9}+i\sin \frac{2880}{9}\right)\\ =5\left(\cos 320+i\sin 320\right)\end{array}$

As, the sine is negative and cosine is positive in the fourth quadrant, then the standard from is written as,

  $\begin{array}{l}=5\left(\cos \left(360-40\right)+i\sin \left(360-40\right)\right)\\ =5\left(\cos 40-i\sin 40\right)\\ =3.8302-3.2140i\end{array}$

(c)

To determine

To graph:

The roots in graphical form.

Explanation of Solution

Given information:

Roots given,

  $5\left(\cos \frac{4\pi }{9}+i\sin \frac{4\pi }{9}\right),5\left(\cos \frac{10\pi }{9}+i\sin \frac{10\pi }{9}\right)$ and $5\left(\cos \frac{16\pi }{9}+i\sin \frac{16\pi }{9}\right)$

Graph:

  

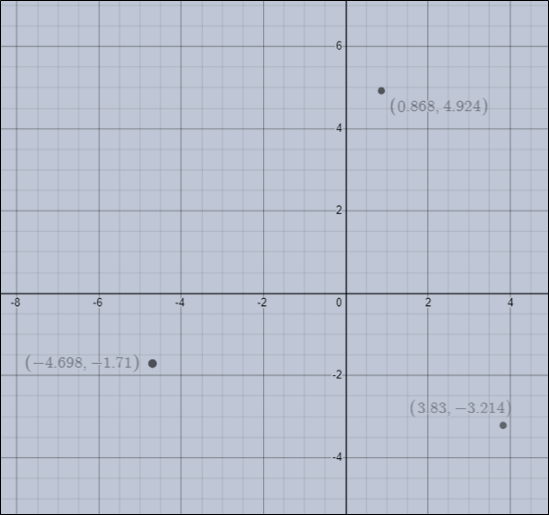
Interpretation:

The roots of the given complex number $5\left(\cos \frac{4\pi }{9}+i\sin \frac{4\pi }{9}\right),5\left(\cos \frac{10\pi }{9}+i\sin \frac{10\pi }{9}\right)$ and $5\left(\cos \frac{16\pi }{9}+i\sin \frac{16\pi }{9}\right)$ are graphed as above.