Chapter 6.5, Problem 23E

To determine

Tofind:the complex number in the form of trigonometric form without using calculator and represent the complex number graphically.

Answer to Problem 23E

  $\text{z=8}\left(\text{cos}\frac{3\pi }{2}\text{+isin}\frac{3\pi }{2}\right)$ .

Explanation of Solution

Given:

  $\text{z=-8i}$ .

Concept used:

Complex form: $\text{z=a+ib}$

In trigonometric form: $\text{z=r}\left(\text{cosθ+isinθ}\right)$

Where, $\text{a=rcosθ}$ and $\text{b=rsinθ}$ .

Modulus: $\text{r=}\sqrt{{\text{a}}^{\text{2}}{\text{+b}}^{\text{2}}}$ .

Argument: ${\text{θ=tan}}^{\text{-1}}\frac{\text{b}}{\text{a}}$ .

And

To plot the graph:

Step 1. Determine the real and imaginary party of the complex number.

Step2. Move along the horizontal axis to show the real part of the number.

Step3. Move parallel to the vertical to show the imaginary part of the number.

Step4. Plot the point.

Calculation:

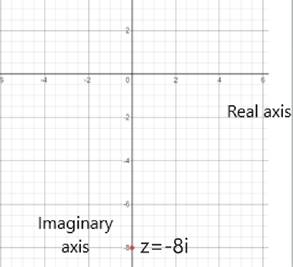
Consider the complex number $\text{z=-8i}$ .

The plot of the complex number is shown below:

  

The trigonometric form of the complex number $\text{z=a+bi}$ is given by:

  $\text{z=r}\left(\text{cosθ+isinθ}\right)$

Here ${\text{θ=tan}}^{\text{-1}}\frac{\text{b}}{\text{a}}$ , $\text{b=rsinθ}$ and $\text{r=}\sqrt{{\text{a}}^{\text{2}}{\text{+b}}^{\text{2}}}$ .

Substituting $\text{a=0 and b=-8}$

Hence,

  ${\text{θ=tan}}^{\text{-1}}\frac{\text{b}}{\text{a}}$

  $\Rightarrow {\text{tan}}^{-1}\frac{-8}{0}$

  $\text{θ=}\frac{\text{3π}}{\text{2}}$

And

  $\text{r=}\sqrt{{\text{a}}^{\text{2}}{\text{+b}}^{\text{2}}}$

  $\text{r=}\sqrt{0^{\text{2}}\text{+}{\left(-8\right)}^{\text{2}}}$

  $\text{r=}\sqrt{\text{64}}$

  $\text{r=8}$ .

Hence the trigonometric form of the complex number $\text{z=-8i}$ is given by:

  $\text{z=8}\left(\text{cos}\frac{3\pi }{2}\text{+isin}\frac{3\pi }{2}\right)$ .