
In Problems 39-47, construct a mathematical model in the form of a linear programming problem. Do not solve.
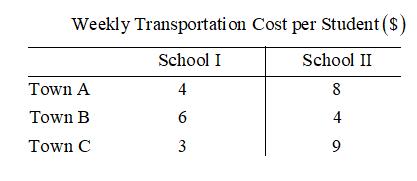
Transportation. Three towns are forming a consolidated school district with two high schools. Each high school has a maximum capacity of
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Finite Mathematics for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
Introductory Statistics
Basic Business Statistics, Student Value Edition
Elementary Statistics
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- How many different passwords are there that contain only digits and lower-case letters and satisfy the given restrictions? (a) Length is 6 and the password must contain at least one digit. (b) Length is 6 and the password must contain at least one digit and at least one letter.arrow_forward1: Neil Mitchell earns $11/hour. During the most recent week, he received a discretionary bonus of $7,200 and worked 43 hours. Gross Pay: $ 7,689.50 2: Francine Palmer earns $7.90/hour. During the most recent week, she received a nondiscretionary bonus of $2,450 and worked 45 hours. Gross Pay: $ 2,825.25 3: Martin Green earns $11.10/hour. During the most recent week, he received a nondiscretionary bonus of $1,360 and worked 51 hours. Gross Pay: $ 1,987.15 4: Melvin Waxman earns $17.60/hour. During the most recent week, he received a nondiscretionary bonus of $440 and worked 56 hours. Gross Pay: $ 1,425.60arrow_forwardObtain the linear equation for trend for time series with St² = 140, Ey = 16.91 and Σty= 62.02, m n = 7arrow_forward
- 1: Kevin Williams earns a weekly wage of $740. During the most recent week, he worked 42 hours. Regular Wage Rate = $ 18.50 Overtime Wage Rate = $ 27.75 2: Charles Joyner earns a biweekly wage of $2,720. During the most recent week, he worked 45 hours. Regular Wage Rate = $ Overtime Wage Rate = $_ 34.00 51.00 3: Julio Valdez earns an annual salary of $81,000. During the most recent week, he worked 44 hours. Regular Wage Rate = $ Overtime Wage Rate = $ 38.94 58.41 4: Bridget Stein earns a monthly salary of $6,200. During the most recent week, she worked 56 hours. Regular Wage Rate = $ 27.50 Overtime Wage Rate = $ 41.25 5: Betsy Cranston earns a semimonthly salary of $2,200. During the most recent week, she worked 49 hours. Regular Wage Rate = $ Overtime Wage Rate = $_ 1,100.00 41.25arrow_forwardIf you are using chatgpt leave it plz Already got wrong chatgpt answer .arrow_forwardSolve themarrow_forward
- 2 prove that Dxy #Dx Dyarrow_forwardEXAMPLE 3 Find S X √√2-2x2 dx. SOLUTION Let u = 2 - 2x². Then du = Χ dx = 2- 2x² = 信 du dx, so x dx = du and u-1/2 du (2√u) + C + C (in terms of x).arrow_forwardLet g(z) = z-i z+i' (a) Evaluate g(i) and g(1). (b) Evaluate the limits lim g(z), and lim g(z). 2-12 (c) Find the image of the real axis under g. (d) Find the image of the upper half plane {z: Iz > 0} under the function g.arrow_forward
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
