a)
To write: an equation that models the height of the ball as a function of time
An equation that models the height of the ball as a function of time
Given information:
The initial velocity is
Formula used:
The formula to find the height of the ball:
Calculation:
Substitute
Hence, an equation that models the height of the ball as a function of time
b)
To simulate: the pop-up.
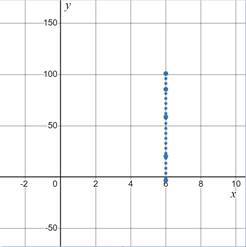
The graph shown below depicts how the ball begins at a height of
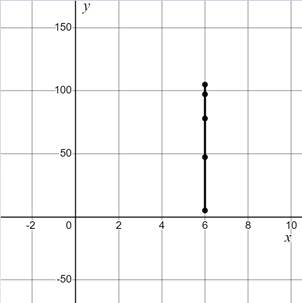
The graph below shows the fall of the ball back to the ground.
Given information:
The initial velocity is
Calculation:
The graph shown below depicts how the ball begins at a height of
The graph below shows the fall of the ball back to the ground.
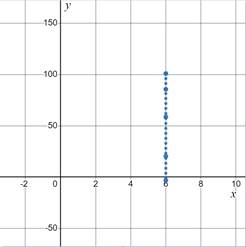
c)
To graph: height against time.
The graph is shown below.

Given information:
The initial velocity is
Calculation:
The graph is shown below.
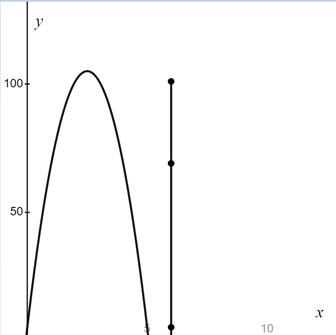
d)
To find: the height of the ball after
After
Given information:
The initial velocity is
Formula used:
The formula to find the height of the ball:
Calculation:
Substitute
After
e)
To find: the maximum height of the ball and how many seconds does it take to reach its maximum height.
The time taken to reach the maximum height
Given information:
The initial velocity is
Formula used:
The formula to find the height of the ball:
Calculation:
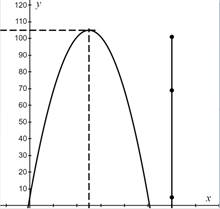
From the graph it is evident that
Therefore, the time taken to reach the maximum height
Chapter 6 Solutions
EBK PRECALCULUS:GRAPHICAL,...-NASTA ED.
- Suppose that f(x, y) = y√√r³ +1 on the domain D = {(x, y) | 0 ≤y≤x≤ 1}. D Then the double integral of f(x, y) over D is [ ], f(x, y)dzdy =[ Round your answer to four decimal places.arrow_forwardConsider the function f(x) = 2x² - 8x + 3 over the interval 0 ≤ x ≤ 9. Complete the following steps to find the global (absolute) extrema on the interval. Answer exactly. Separate multiple answers with a comma. a. Find the derivative of f (x) = 2x² - 8x+3 f'(x) b. Find any critical point(s) c within the intervl 0 < x < 9. (Enter as reduced fraction as needed) c. Evaluate the function at the critical point(s). (Enter as reduced fraction as needed. Enter DNE if none of the critical points are inside the interval) f(c) d. Evaluate the function at the endpoints of the interval 0 ≤ x ≤ 9. f(0) f(9) e. Based on the above results, find the global extrema on the interval and where they occur. The global maximum value is at a The global minimum value is at xarrow_forwardDetermine the values and locations of the global (absolute) and local extrema on the graph given. Assume the domain is a closed interval and the graph represents the entirety of the function. 3 y -6-5-4-3 2 1 -1 -2 -3 Separate multiple answers with a comma. Global maximum: y Global minimum: y Local maxima: y Local minima: y x 6 at a at a at x= at x=arrow_forward
- A ball is thrown into the air and its height (in meters) is given by h (t) in seconds. -4.92 + 30t+1, where t is a. After how long does the ball reach its maximum height? Round to 2 decimal places. seconds b. What is the maximum height of the ball? Round to 2 decimal places. metersarrow_forwardDetermine where the absolute and local extrema occur on the graph given. Assume the domain is a closed interval and the graph represents the entirety of the function. 1.5 y 1 0.5 -3 -2 -0.5 -1 -1.5 Separate multiple answers with a comma. Absolute maximum at Absolute minimum at Local maxima at Local minima at a x 2 3 аarrow_forwardA company that produces cell phones has a cost function of C = x² - 1000x + 36100, where C is the cost in dollars and x is the number of cell phones produced (in thousands). How many units of cell phones (in thousands) minimizes this cost function? Round to the nearest whole number, if necessary. thousandarrow_forward
- Under certain conditions, the number of diseased cells N(t) at time t increases at a rate N'(t) = Aekt, where A is the rate of increase at time 0 (in cells per day) and k is a constant. (a) Suppose A = 60, and at 3 days, the cells are growing at a rate of 180 per day. Find a formula for the number of cells after t days, given that 200 cells are present at t = 0. (b) Use your answer from part (a) to find the number of cells present after 8 days. (a) Find a formula for the number of cells, N(t), after t days. N(t) = (Round any numbers in exponents to five decimal places. Round all other numbers to the nearest tenth.)arrow_forwardThe marginal revenue (in thousands of dollars) from the sale of x handheld gaming devices is given by the following function. R'(x) = 4x (x² +26,000) 2 3 (a) Find the total revenue function if the revenue from 125 devices is $17,939. (b) How many devices must be sold for a revenue of at least $50,000? (a) The total revenue function is R(x) = (Round to the nearest integer as needed.) given that the revenue from 125 devices is $17,939.arrow_forwardUse substitution to find the indefinite integral. S 2u √u-4 -du Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice. A. Substitute u for the quantity in the numerator. Let v = , so that dv = ( ) du. B. Substitute u for the quantity under the root. Let v = u-4, so that dv = (1) du. C. Substitute u for the quantity in the denominator. Let v = Use the substitution to evaluate the integral. so that dv= ' ( du. 2u -du= √√u-4arrow_forward
- Use substitution to find the indefinite integral. Зи u-8 du Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice. A. Substitute u for the quantity in the numerator. Let v = , so that dv = ( ( ) du. B. Substitute u for the quantity under the root. Let v = u-8, so that dv = (1) du. C. Substitute u for the quantity in the denominator. Let v = so that dv= ( ) du. Use the substitution to evaluate the integral. S Зи -du= u-8arrow_forwardFind the derivative of the function. 5 1 6 p(x) = -24x 5 +15xarrow_forward∞ 2n (4n)! Let R be the radius of convergence of the series -x2n. Then the value of (3" (2n)!)² n=1 sin(2R+4/R) is -0.892 0.075 0.732 -0.812 -0.519 -0.107 -0.564 0.588arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





