EP THINKING MATHEMATICALLY-ACCESS
7th Edition
ISBN: 9780135963388
Author: Blitzer
Publisher: PEARSON CO
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.3, Problem 1CP
CHECK POINT 1 The average yearly salary of a woman with a bachelor’s degree exceeds that of a woman with an associate’s degree by $14 thousand. The Average yearly salary of a woman with a master’s degree exceeds that of a coman with an associate’s degree by $26 thousand. Combined, three women with each of these educational attainments earn $139 thousand. Find the average yearly salary of women with each of these levels of education. (These salaries are illustrated by the bar graph on page 370.)
Expert Solution & Answer
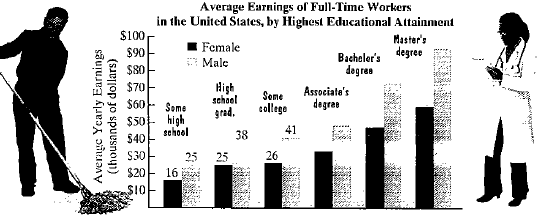
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Part 1 and 2
Advanced Functional Analysis Mastery Quiz
Instructions:
.
No partial credit will be awarded; any mistake will result in a score of 0.
Submit your solution before the deadline.
Ensure your solution is detailed, and all steps are well-documented
No Al tools (such as Chat GPT or others) may be used to assist in solving the problems. All work
must be your own.
Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a
score of 0.
Problem
Let X and Y be Banach spaces, and T: XY be a bounded linear operator. Consider the
following tasks
1. [Operator Norm and Boundedness] a. Prove that for any bounded linear operator T: XY
the norm of satisfies:
Tsup ||T(2)||.
2-1
b. Show that if T' is a bounded linear operator on a Banach space and T <1, then the
operatur 1-T is inverüble, and (IT) || ST7
2. [Weak and Strong Convergence] a Define weak and strong convergence in a Banach space .X.
Provide examples of sequences that converge weakly but not strongly, and vice…
Part 1 and 2
Chapter 6 Solutions
EP THINKING MATHEMATICALLY-ACCESS
Ch. 6.1 - CHECK POINT 1 Evaluate .
Ch. 6.1 - CHECK POINT 2 Evaluate x 2 + 4 x − 7 for x = −...Ch. 6.1 - CHECK POINT 3 Evaluate − 3 x 2 + 4 x y − y 3 for...Ch. 6.1 - CHECK POINT 4 The mathematic model M = − 120 x 2 +...Ch. 6.1 - Prob. 5CPCh. 6.1 - CHECK POINT 6 Simplify: 7 ( 4 x 2 + 3 x ) + 2 ( 5...Ch. 6.1 - Prob. 7CPCh. 6.1 - Fill in each blank so that the resulting statement...Ch. 6.1 - Fill in each blank so that the resulting statement...Ch. 6.1 - Fill in each blank so that the resulting statement...
Ch. 6.1 - Prob. 4CVCCh. 6.1 - Prob. 5CVCCh. 6.1 - Prob. 6CVCCh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 3ECh. 6.1 - Prob. 4ECh. 6.1 - Prob. 5ECh. 6.1 - Prob. 6ECh. 6.1 - Prob. 7ECh. 6.1 - Prob. 8ECh. 6.1 - Prob. 9ECh. 6.1 - Prob. 10ECh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 12ECh. 6.1 - Prob. 13ECh. 6.1 - Prob. 14ECh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 16ECh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 24ECh. 6.1 - Prob. 25ECh. 6.1 - Prob. 26ECh. 6.1 - Prob. 27ECh. 6.1 - Prob. 28ECh. 6.1 - Prob. 29ECh. 6.1 - Prob. 30ECh. 6.1 - Prob. 31ECh. 6.1 - Prob. 32ECh. 6.1 - Prob. 33ECh. 6.1 - Prob. 34ECh. 6.1 - The formula C = 5 9 ( F − 32 ) expresses the...Ch. 6.1 - Prob. 36ECh. 6.1 - Prob. 37ECh. 6.1 - Prob. 38ECh. 6.1 - In Exercises 39-40, name the property used to go...Ch. 6.1 - Prob. 40ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 42ECh. 6.1 - Prob. 43ECh. 6.1 - Prob. 44ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 47ECh. 6.1 - Prob. 48ECh. 6.1 - Prob. 49ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 51ECh. 6.1 - Prob. 52ECh. 6.1 - Prob. 53ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 56ECh. 6.1 - Prob. 57ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 59ECh. 6.1 - Prob. 60ECh. 6.1 - Prob. 61ECh. 6.1 - Prob. 62ECh. 6.1 - Prob. 63ECh. 6.1 - Prob. 64ECh. 6.1 - Prob. 65ECh. 6.1 - Prob. 66ECh. 6.1 - 67. If you exercise goal is to improve...Ch. 6.1 - Prob. 68ECh. 6.1 - The bar graph shows the estimated number of...Ch. 6.1 - Prob. 70ECh. 6.1 - Prob. 71ECh. 6.1 - Source: MonsterCollege TM The mathematical model p...Ch. 6.1 - Read the Blitzer Bonus on page 346. Use the...Ch. 6.1 - Prob. 74ECh. 6.1 - Prob. 75ECh. 6.1 - Prob. 76ECh. 6.1 - Prob. 77ECh. 6.1 - Prob. 78ECh. 6.1 - Prob. 79ECh. 6.1 - Prob. 80ECh. 6.1 - Prob. 81ECh. 6.1 - Prob. 82ECh. 6.1 - Prob. 83ECh. 6.1 - Prob. 84ECh. 6.1 - Prob. 85ECh. 6.1 - Prob. 86ECh. 6.1 - Prob. 87ECh. 6.1 - Prob. 88ECh. 6.1 - Prob. 89ECh. 6.1 - Prob. 90ECh. 6.1 - Prob. 91ECh. 6.1 - Prob. 92ECh. 6.1 - A business that manufactures small alarm clocks...Ch. 6.2 - CHECK POINT 1 Solve and check:
Ch. 6.2 - CHECK POINT 2 Solve and check: 6 ( x − 3 ) − 10 x...Ch. 6.2 - CHECK POINT 3 Solve the equation: 2 x + 9 = 8 x −...Ch. 6.2 - CHECK POINT 4 Solve and check: 4 ( 2 x + 1 ) = 29...Ch. 6.2 - CHECK POINT 5 Solve and check: 2 x 3 = 7 − x 2 .Ch. 6.2 - CHECK POINT 6 Use the model the low-humor group...Ch. 6.2 - $$ CHECK POINT 7 Solve each proportion and check:...Ch. 6.2 - CHECK POINT 8 The property tax on a house with an...Ch. 6.2 - CHECK POINT 9 Wildlife biologists catch, tag and...Ch. 6.2 - CHECK POINT 10 Solve: 3 x + 7 = 3 ( x + 1 ) .Ch. 6.2 - CHECK POINT 11 Solve: .
Ch. 6.2 - 1. An equation in the form such as is called...Ch. 6.2 - 2. Two or more equations that have the same...Ch. 6.2 - 3. The addition property of equality states that...Ch. 6.2 - 4. The multiplication property of equality states...Ch. 6.2 - 5. The first step in solving is to ____.
Ch. 6.2 - 6. The algebraic expression can be ____, whereas...Ch. 6.2 - The equation x 4 = 2 + x 3 can be cleared of...Ch. 6.2 - A statement that two ratios are equal is called...Ch. 6.2 - The cross-products principle states that if a b =...Ch. 6.2 - In solving an equation, if you eliminate the...Ch. 6.2 - 11. In solving an equation with variable x, if you...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 2ECh. 6.2 - Prob. 3ECh. 6.2 - Prob. 4ECh. 6.2 - Prob. 5ECh. 6.2 - Prob. 6ECh. 6.2 - Prob. 7ECh. 6.2 - Prob. 8ECh. 6.2 - Prob. 9ECh. 6.2 - Prob. 10ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 12ECh. 6.2 - Prob. 13ECh. 6.2 - Prob. 14ECh. 6.2 - Prob. 15ECh. 6.2 - Prob. 16ECh. 6.2 - Prob. 17ECh. 6.2 - Prob. 18ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 20ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 22ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - Prob. 27ECh. 6.2 - Prob. 28ECh. 6.2 - Prob. 29ECh. 6.2 - Prob. 30ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 32ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 34ECh. 6.2 - Prob. 35ECh. 6.2 - Prob. 36ECh. 6.2 - Prob. 37ECh. 6.2 - Prob. 38ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 40ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 42ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 46ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 48ECh. 6.2 - Prob. 49ECh. 6.2 - Prob. 50ECh. 6.2 - Prob. 51ECh. 6.2 - Prob. 52ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 56ECh. 6.2 - Prob. 57ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 60ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 62ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 64ECh. 6.2 - Prob. 65ECh. 6.2 - Prob. 66ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 68ECh. 6.2 - Prob. 69ECh. 6.2 - Prob. 70ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 73ECh. 6.2 - Prob. 74ECh. 6.2 - Prob. 75ECh. 6.2 - Prob. 76ECh. 6.2 - Prob. 77ECh. 6.2 - Prob. 78ECh. 6.2 - Prob. 79ECh. 6.2 - Prob. 80ECh. 6.2 - Prob. 81ECh. 6.2 - Prob. 82ECh. 6.2 - Prob. 83ECh. 6.2 - Prob. 84ECh. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - Prob. 88ECh. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - Prob. 90ECh. 6.2 - Prob. 91ECh. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - Prob. 93ECh. 6.2 - Prob. 94ECh. 6.2 - Prob. 95ECh. 6.2 - 96. Evaluate for x satisfying and y satisfying...Ch. 6.2 - Prob. 97ECh. 6.2 - In Exercises 97- 104, solve each equation.
98.
Ch. 6.2 - Prob. 99ECh. 6.2 - Prob. 100ECh. 6.2 - Prob. 101ECh. 6.2 - Prob. 102ECh. 6.2 - Prob. 103ECh. 6.2 - Prob. 104ECh. 6.2 - The mathematical model
describe a weight, W in...Ch. 6.2 - The mathematical model W 2 − 3 H = 53 describe a...Ch. 6.2 - Grade Inflation. The bar graph shows the...Ch. 6.2 - Grade Inflation. The bar graph shows the...Ch. 6.2 - 109. The volume of blood in a person’s body is...Ch. 6.2 - Prob. 110ECh. 6.2 - 111. An alligator’s tail length is proportional to...Ch. 6.2 - 112. An object’s weight on the moon is...Ch. 6.2 - Prob. 113ECh. 6.2 - 114. To estimate the number of base in a lake,...Ch. 6.2 - Prob. 115ECh. 6.2 - State the addition property of equality and give...Ch. 6.2 - Prob. 117ECh. 6.2 - Prob. 118ECh. 6.2 - Prob. 119ECh. 6.2 - Prob. 120ECh. 6.2 - Prob. 121ECh. 6.2 - Prob. 122ECh. 6.2 - Prob. 123ECh. 6.2 - Prob. 124ECh. 6.2 - Prob. 125ECh. 6.2 - Prob. 126ECh. 6.2 - Prob. 127ECh. 6.2 - Prob. 128ECh. 6.2 - 129. Write three equations whose solution set is...Ch. 6.2 - 130. If x represent a number, write an English...Ch. 6.2 - 131. A woman’s height, h, is related to the length...Ch. 6.3 - CHECK POINT 1 The average yearly salary of a woman...Ch. 6.3 - Prob. 2CPCh. 6.3 - CHECK POINT 3 The toll to a bridge costs $5....Ch. 6.3 - CHECK POINT 4 After a 30% price reducing, you...Ch. 6.3 - Prob. 5CPCh. 6.3 - Prob. 6CPCh. 6.3 - 1. According to the U.S. Office of Management and...Ch. 6.3 - In 2000, 31% of U.S. adults viewed a college...Ch. 6.3 - Prob. 3CVCCh. 6.3 - Prob. 4CVCCh. 6.3 - Prob. 5CVCCh. 6.3 - Prob. 6CVCCh. 6.3 - Use the five-step strategy for solving word...Ch. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Prob. 3ECh. 6.3 - Prob. 4ECh. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Prob. 8ECh. 6.3 - Prob. 9ECh. 6.3 - Prob. 10ECh. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - Prob. 12ECh. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - Prob. 17ECh. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - How will you spend your average life expectancy of...Ch. 6.3 - How will you spend your average life expectancy of...Ch. 6.3 - The bar graph shows average yearly earnings in the...Ch. 6.3 - The bar graph shows average yearly earnings in the...Ch. 6.3 - Prob. 23ECh. 6.3 - Prob. 24ECh. 6.3 - On average, every minute of every day, 158 babies...Ch. 6.3 - On average, every minute of every day, 158 babies...Ch. 6.3 - Prob. 27ECh. 6.3 - Prob. 28ECh. 6.3 - Prob. 29ECh. 6.3 - You need to rent a rug cleaner. Company A will...Ch. 6.3 - Prob. 31ECh. 6.3 - Prob. 32ECh. 6.3 - Prob. 33ECh. 6.3 - Prob. 34ECh. 6.3 - Prob. 35ECh. 6.3 - Prob. 36ECh. 6.3 - Prob. 37ECh. 6.3 - Prob. 38ECh. 6.3 - Prob. 39ECh. 6.3 - Prob. 40ECh. 6.3 - Prob. 41ECh. 6.3 - Prob. 42ECh. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - Prob. 44ECh. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - Prob. 58ECh. 6.3 - Prob. 59ECh. 6.3 - Prob. 60ECh. 6.3 - Prob. 61ECh. 6.3 - Prob. 62ECh. 6.3 - Prob. 63ECh. 6.3 - Prob. 64ECh. 6.3 - Make Sense? In Exercises 65-68, determine whether...Ch. 6.3 - Make Sense? In Exercises 65-68, determine whether...Ch. 6.3 - Prob. 67ECh. 6.3 - Prob. 68ECh. 6.3 - Prob. 69ECh. 6.3 - Prob. 70ECh. 6.3 - Prob. 71ECh. 6.3 - Prob. 72ECh. 6.3 - A thief steals a number of rare plants from a...Ch. 6.3 - Prob. 74ECh. 6.3 - Prob. 75ECh. 6.3 - One of the best ways to learn how to solve a word...Ch. 6.4 - $$ CHECK POINT I Graph each set: a. { x | x < 4 }...Ch. 6.4 - Prob. 2CPCh. 6.4 - Prob. 3CPCh. 6.4 - Prob. 4CPCh. 6.4 - Prob. 5CPCh. 6.4 - Prob. 6CPCh. 6.4 - Prob. 7CPCh. 6.4 - 1. On a number line, an open dot indicates that a...Ch. 6.4 - 2. If an inequality’s solution set consists of...Ch. 6.4 - 3. If an inequality’s solution set consists of all...Ch. 6.4 - Prob. 4CVCCh. 6.4 - Prob. 5CVCCh. 6.4 - Prob. 6CVCCh. 6.4 - Prob. 7CVCCh. 6.4 - In Exercises 5-8, determine whether each statement...Ch. 6.4 - In Exercises 1-12, graph each set of real numbers...Ch. 6.4 - Prob. 2ECh. 6.4 - Prob. 3ECh. 6.4 - In Exercises 1-12, graph each set of real numbers...Ch. 6.4 - Prob. 5ECh. 6.4 - Prob. 6ECh. 6.4 - Prob. 7ECh. 6.4 - Prob. 8ECh. 6.4 - Prob. 9ECh. 6.4 - Prob. 10ECh. 6.4 - Prob. 11ECh. 6.4 - Prob. 12ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 30ECh. 6.4 - Prob. 31ECh. 6.4 - Prob. 32ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 34ECh. 6.4 - Prob. 35ECh. 6.4 - Prob. 36ECh. 6.4 - Prob. 37ECh. 6.4 - Prob. 38ECh. 6.4 - Prob. 39ECh. 6.4 - Prob. 40ECh. 6.4 - Prob. 41ECh. 6.4 - Prob. 42ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 52ECh. 6.4 - Prob. 53ECh. 6.4 - Prob. 54ECh. 6.4 - Prob. 55ECh. 6.4 - Prob. 56ECh. 6.4 - Prob. 57ECh. 6.4 - Prob. 58ECh. 6.4 - Prob. 59ECh. 6.4 - Prob. 60ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 64ECh. 6.4 - Prob. 65ECh. 6.4 - Prob. 66ECh. 6.4 - Prob. 67ECh. 6.4 - Prob. 68ECh. 6.4 - Prob. 69ECh. 6.4 - Prob. 70ECh. 6.4 - In Exercises 71-76, use set-builder notation to...Ch. 6.4 - Prob. 72ECh. 6.4 - Prob. 73ECh. 6.4 - Prob. 74ECh. 6.4 - Prob. 75ECh. 6.4 - Prob. 76ECh. 6.4 - Prob. 77ECh. 6.4 - Prob. 78ECh. 6.4 - The graphs show that the three components of love,...Ch. 6.4 - Prob. 80ECh. 6.4 - Prob. 81ECh. 6.4 - The graphs show that the three components of love,...Ch. 6.4 - Prob. 83ECh. 6.4 - Prob. 84ECh. 6.4 - models the percentage of U.S. households in which...Ch. 6.4 - Prob. 86ECh. 6.4 - Prob. 87ECh. 6.4 - Prob. 88ECh. 6.4 - Prob. 89ECh. 6.4 - Prob. 90ECh. 6.4 - Prob. 91ECh. 6.4 - Prob. 92ECh. 6.4 - Prob. 93ECh. 6.4 - Prob. 94ECh. 6.4 - Prob. 95ECh. 6.4 - Prob. 96ECh. 6.4 - Prob. 97ECh. 6.4 - Prob. 98ECh. 6.4 - Prob. 99ECh. 6.4 - Prob. 100ECh. 6.4 - Prob. 101ECh. 6.4 - Prob. 102ECh. 6.4 - Prob. 103ECh. 6.4 - Prob. 104ECh. 6.5 - CHECK POINT 1 Multiple:
Ch. 6.5 - CHECK POINT 2 Multiple: ( 7 x + 5 ) ( 4 x − 3 )Ch. 6.5 - Prob. 3CPCh. 6.5 - Prob. 4CPCh. 6.5 - CHECK POINT 5 Factor: 5 x 2 − 14 x + 8Ch. 6.5 - Prob. 6CPCh. 6.5 - Prob. 7CPCh. 6.5 - Prob. 8CPCh. 6.5 - Prob. 9CPCh. 6.5 - Prob. 10CPCh. 6.5 - Prob. 11CPCh. 6.5 - Prob. 12CPCh. 6.5 - Prob. 1CVCCh. 6.5 - Prob. 2CVCCh. 6.5 - Prob. 3CVCCh. 6.5 - Prob. 4CVCCh. 6.5 - Prob. 5CVCCh. 6.5 - Prob. 6CVCCh. 6.5 - Prob. 7CVCCh. 6.5 - Prob. 8CVCCh. 6.5 - Prob. 9CVCCh. 6.5 - Prob. 10CVCCh. 6.5 - The zero-product principle states that if A B = 0...Ch. 6.5 - Prob. 12CVCCh. 6.5 - Prob. 13CVCCh. 6.5 - Prob. 14CVCCh. 6.5 - Prob. 15CVCCh. 6.5 - Prob. 16CVCCh. 6.5 - Prob. 17CVCCh. 6.5 - Prob. 18CVCCh. 6.5 - Prob. 1ECh. 6.5 - Prob. 2ECh. 6.5 - Prob. 3ECh. 6.5 - Prob. 4ECh. 6.5 - Prob. 5ECh. 6.5 - Prob. 6ECh. 6.5 - Prob. 7ECh. 6.5 - Prob. 8ECh. 6.5 - Prob. 9ECh. 6.5 - Prob. 10ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 12ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 14ECh. 6.5 - Prob. 15ECh. 6.5 - Prob. 16ECh. 6.5 - Prob. 17ECh. 6.5 - Prob. 18ECh. 6.5 - Prob. 19ECh. 6.5 - Prob. 20ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 22ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 24ECh. 6.5 - Prob. 25ECh. 6.5 - Prob. 26ECh. 6.5 - Prob. 27ECh. 6.5 - Prob. 28ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 30ECh. 6.5 - Prob. 31ECh. 6.5 - Prob. 32ECh. 6.5 - In Exercises 33-36, solve each equation using the...Ch. 6.5 - Prob. 34ECh. 6.5 - In Exercises 33-36, solve each equation using the...Ch. 6.5 - Prob. 36ECh. 6.5 - Solve the quadratic equations in Exercises 37-52,...Ch. 6.5 - Prob. 38ECh. 6.5 - Prob. 39ECh. 6.5 - Prob. 40ECh. 6.5 - Prob. 41ECh. 6.5 - Prob. 42ECh. 6.5 - Prob. 43ECh. 6.5 - Prob. 44ECh. 6.5 - Prob. 45ECh. 6.5 - Prob. 46ECh. 6.5 - Prob. 47ECh. 6.5 - Prob. 48ECh. 6.5 - Prob. 49ECh. 6.5 - Prob. 50ECh. 6.5 - Prob. 51ECh. 6.5 - Prob. 52ECh. 6.5 - Prob. 53ECh. 6.5 - Prob. 54ECh. 6.5 - Solve the equations in Exercises 53-72 using the...Ch. 6.5 - Prob. 56ECh. 6.5 - Prob. 57ECh. 6.5 - Prob. 58ECh. 6.5 - Prob. 59ECh. 6.5 - Prob. 60ECh. 6.5 - Prob. 61ECh. 6.5 - Prob. 62ECh. 6.5 - Prob. 63ECh. 6.5 - Prob. 64ECh. 6.5 - Prob. 65ECh. 6.5 - Prob. 66ECh. 6.5 - Prob. 67ECh. 6.5 - Prob. 68ECh. 6.5 - Prob. 69ECh. 6.5 - Prob. 70ECh. 6.5 - Prob. 71ECh. 6.5 - Prob. 72ECh. 6.5 - Prob. 73ECh. 6.5 - Prob. 74ECh. 6.5 - Prob. 75ECh. 6.5 - Prob. 76ECh. 6.5 - Prob. 77ECh. 6.5 - Prob. 78ECh. 6.5 - Prob. 79ECh. 6.5 - Prob. 80ECh. 6.5 - Prob. 81ECh. 6.5 - Prob. 82ECh. 6.5 - Prob. 83ECh. 6.5 - Prob. 84ECh. 6.5 - Prob. 85ECh. 6.5 - Prob. 86ECh. 6.5 - Prob. 87ECh. 6.5 - Prob. 88ECh. 6.5 - 89. Explain how to factor .
Ch. 6.5 - Prob. 90ECh. 6.5 - Prob. 91ECh. 6.5 - Prob. 92ECh. 6.5 - Prob. 93ECh. 6.5 - Prob. 94ECh. 6.5 - Prob. 95ECh. 6.5 - Prob. 96ECh. 6.5 - The radicand of the quadratic formula, b 2 − 4 a c...Ch. 6.5 - Prob. 98ECh. 6.5 - In Exercises 98-99, find all positive integers b...Ch. 6.5 - Prob. 100ECh. 6.5 - Prob. 101ECh. 6 - In Exercises 1-3, evaluate the algebraic...Ch. 6 - In Exercises 1-3, evaluate the algebraic...Ch. 6 - Prob. 3RECh. 6 - Prob. 4RECh. 6 - In Exercises 5-7, simplify each algebraic...Ch. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - Prob. 11RECh. 6 - Prob. 12RECh. 6 - Prob. 13RECh. 6 - Prob. 14RECh. 6 - Prob. 15RECh. 6 - In Exercises 15-18, solve each proportion.
16.
Ch. 6 - Prob. 17RECh. 6 - Prob. 18RECh. 6 - Prob. 19RECh. 6 - 20. To determine the number of trout in a lake, a...Ch. 6 - 21. The line graph showy he cost of inflation....Ch. 6 - Prob. 22RECh. 6 - Prob. 23RECh. 6 - 24. You are choosing between two cellphone plans....Ch. 6 - Prob. 25RECh. 6 - Prob. 26RECh. 6 - Prob. 27RECh. 6 - Prob. 28RECh. 6 - Prob. 29RECh. 6 - Prob. 30RECh. 6 - Prob. 31RECh. 6 - Prob. 32RECh. 6 - Prob. 33RECh. 6 - Prob. 34RECh. 6 - Prob. 35RECh. 6 - Prob. 36RECh. 6 - In Exercises 31-37, solve each inequality and...Ch. 6 - Prob. 38RECh. 6 - Prob. 39RECh. 6 - Prob. 40RECh. 6 - Prob. 41RECh. 6 - Prob. 42RECh. 6 - Prob. 43RECh. 6 - Prob. 44RECh. 6 - Prob. 45RECh. 6 - Prob. 46RECh. 6 - Prob. 47RECh. 6 - Prob. 48RECh. 6 - Prob. 49RECh. 6 - Prob. 50RECh. 6 - Prob. 51RECh. 6 - Prob. 52RECh. 6 - Prob. 53RECh. 6 - Prob. 54RECh. 6 - Prob. 55RECh. 6 - 1. Evaluate when .
Ch. 6 - Prob. 2TCh. 6 - Prob. 3TCh. 6 - Prob. 4TCh. 6 - Prob. 5TCh. 6 - Prob. 6TCh. 6 - Prob. 7TCh. 6 - Prob. 8TCh. 6 - Prob. 9TCh. 6 - Prob. 10TCh. 6 - Prob. 11TCh. 6 - Prob. 12TCh. 6 - Prob. 13TCh. 6 - Prob. 14TCh. 6 - Prob. 15TCh. 6 - Prob. 16TCh. 6 - Prob. 17TCh. 6 - Prob. 18TCh. 6 - Prob. 19TCh. 6 - Prob. 20TCh. 6 - Prob. 21TCh. 6 - Prob. 22TCh. 6 - Prob. 23TCh. 6 - Prob. 24TCh. 6 - Prob. 25TCh. 6 - Prob. 26T
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...
Precalculus: Mathematics for Calculus (Standalone Book)
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
NOTE: Write your answers using interval notation when appropriate.
CHECKING ANALYTIC SKILLS Fill in each blank ...
Graphical Approach To College Algebra
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- please solve handwritten without use of AIarrow_forwardYou’re scrolling through Instagram and you notice that a lot of people are posting selfies. This piques yourcuriosity and you want to estimate the percentage of photos on Instagram that are selfies.(a) (5 points) Is there a “ground truth” for the percentage of selfies on Instagram? Why or why not?(b) (5 points) Is it possible to estimate the ground truth percentage of selfies on Instagram?Irrespective of your answer to the previous question, you decide to pull up n = 250 randomly chosenphotos from your friends’ Instagram accounts and find that 32% of these photos are selfies.(c) (15 points) Determine which of the following is an observation, a variable, a sample statistic (valuecalculated based on the observed sample), or a population parameter.• A photo on Instagram.• Whether or not a photo is a selfie.• Percentage of all photos on Instagram that are selfies.• 32%.(d) (5 points) Based on the sample you collected, do you think 32% is a reliable ballpark estimate for theground truth…arrow_forwardPart 1 and 2arrow_forward
- Part 1 and 2arrow_forwardAdvanced Mathematics Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. . Submit your solution before the deadline. • Ensure your solution is detailed, and all steps are well-documented. . No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let the function f(x, y, z) = r³y-2xy + 3yz² +e+y+ and consider the following tasks: 1. [Critical Points and Classification] a. Find all critical points of f(x, y, z). b. Use the second partial derivative test to classify each critical point as a local minimum, local maximum, or saddle point. 2. [Gradient and Divergence] a. Compute the gradient vector Vf. b. Calculate the divergence of the gradient field and explain its significance. 3. [Line Integral Evaluation] Consider the vector field F(x, y, z) = (e² + yz, x²y ar). a.…arrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. ⚫ Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. • No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X te a Banach space, and let T: XX be a linear operetor satisfying ||T|| - 1. Corsider the following tasks: 1. [Bounded Linear Operators] a. Prove that I is a bounded linear operator if and only if there exists a constant C such that ||T()||C|||| for all 2 € X. b. Show that if I' is a linear operator on a Banach space X and ||T||-1, then ||T(x)||||||| for all EX. 2. [Spectral Theorem] Let A be a self-adjoint operator on a Hibert space H. Assume that A has a non-empty spectrum. a. State and prove the Spectral…arrow_forward
- Advanced Mathematics Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. . . No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let the function f(x, y, z)=-42y+2ay" +22 tasks: and consider the following 1. [Critical Points and Classification] a. Find all critical points of f(x, y, z). b. Use the second partial derivative test to classify each critical point as a local minimum, local maximum, or saddle point. 2. [Directional Derivatives and Gradients] a. Compute the gradient vector Vf of f(x, y, z). b. Find the directional derivative of f at the point (1, 1, 1) in the direction of the vector v = (1,-2,3). 3. [Line Integral Evaluation] Consider the…arrow_forwardQ11. A president and a treasurer are to be chosen from a student club consisting of 50 people. How many different choices of officers are possible if (a) there are no restrictions (b) A will serve only if he is president (c) B and C will serve together or not at allarrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: . . No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. . . No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X and Y be Banach spaces, and let T: XY be a bounded linear operator. Consider the following tasks: 1. [Baire's Category Theorem and Applications] a. State and prove Baire's Category Theorem for Banach spaces. Use the theorem to prove that a complete metric space cannot be the countable union of nowhere dense sets. b. Use Baire's Category Theorem to show that if T: XY is a bounded linear operator between Banach spaces, then the set of points in X where I' is continuous is a dense G8 set. 2. [Norms and…arrow_forward
- Advanced Functional Analysis Mastery Quiz Instructions: No partial credit will be awarded; any mistake will result in a score of 0. . Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X be a Banach space, and 7' be a bounded linear operator acting on X. Consider the following tasks: 1. [Operator Norm and Boundedness] a. Prove that the operator norm of a linear operator T': X →→ X is given by: ||T|| =sup ||T(2)|| 2-1 b. Show that if 'T' is a bounded linear operator on a Banach space, then the sequence {7"} converges to zero pointwise on any bounded subset of X if and only if ||T|| p, from X to X, where 4, (y)=(x, y), is a linear operator. b. Consider a sequence {} CX. Prove that if →→ 6(2)→→ (2)…arrow_forwardSolve this differential equation: dy 0.05y(900 - y) dt y(0) = 2 y(t) =arrow_forwardMathematics Challenge Quiz Instructions: • You must submit your solution before the deadline. • Any mistake will result in a score of 0 for this quiz. • Partial credit is not allowed; ensure your answer is complete and accurate. Problem Consider the parametric equations: x(t) = e cos(3t), y(t) = e sin(3t) fort Є R. 1. [Parametric Curve Analysis] a. Prove that the parametric curve represents a spiral by eliminating t and deriving the general equation in Cartesian form. b. Find the curvature (t) of the curve at any point 1. 2. [Integral Evaluation] For the region enclosed by the spiral between t = 0 and t =π, compute the area using the formula: where t₁ = 0 and t₂ = . A == √ √ ²x²(1)y (t) − y(t) x' (t)] dt 3. [Differential Equation Application] The curve satisfies a differential equation of the form: d'y da2 dy + P(x)+q(x)y = 0 a. Derive the explicit forms of p(x) and q(2). b. Verify your solution by substituting (t) and y(t) into the differential equation. 4. [Optimization and Limits]…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Finite Math: Markov Chain Example - The Gambler's Ruin; Author: Brandon Foltz;https://www.youtube.com/watch?v=afIhgiHVnj0;License: Standard YouTube License, CC-BY
Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra; Author: AfterMath;https://www.youtube.com/watch?v=qK-PUTuUSpw;License: Standard Youtube License
Stochastic process and Markov Chain Model | Transition Probability Matrix (TPM); Author: Dr. Harish Garg;https://www.youtube.com/watch?v=sb4jo4P4ZLI;License: Standard YouTube License, CC-BY