
a.
To determine: the probability of
The probabilities for the value of
Given information:
An average of 7 gopher holes appears on the farm shown each week.
Concept Used:
Probability:
It is the ratio of number of ways it can happen to the total number of outcomes:
Binomial Experiment Probability:
The probability of k successes in the n trials for a binomial experiment is given by
Calculation:
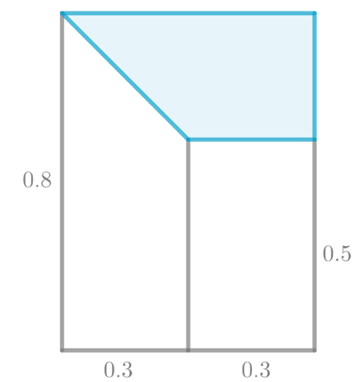
Let x represents the number of animal pits in the market plot.
The total area of the land where the animal pits might appear is
The area of the marked plot is made of a rectangle with sides 0.3 and 0.8-0.5, and a right triangle sides 0.3 and 0.8-0.5.
Therefore, the area of the plot is calculated as the sum of the areas of the rectangle and the triangle:
The general probability of a pit appearing in the plot is determine by dividing the area of the plot with the total area of the land.
Now, calculate the chance for each number of pits or for each value of x , using the formula for binomial probability distribution.
b.
To make: a table for showing the probability distribution for X.
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X) | 0.099 | 0.271 | 0.319 | 0.208 | 0.081 | 0.019 | 0.0025 | 0.0001 |
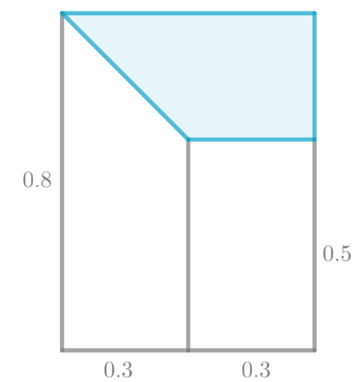
Given information:
An average of 7 gopher holes appears on the farm shown each week.
Concept Used:
Probability:
It is the ratio of number of ways it can happen to the total number of outcomes:
Binomial Experiment Probability:
The probability of k successes in the n trials for a binomial experiment is given by
Calculation:
From the previous part, the probabilities for the value of
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X) | 0.099 | 0.271 | 0.319 | 0.208 | 0.081 | 0.019 | 0.0025 | 0.0001 |
c.
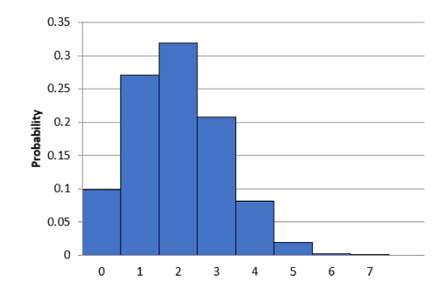
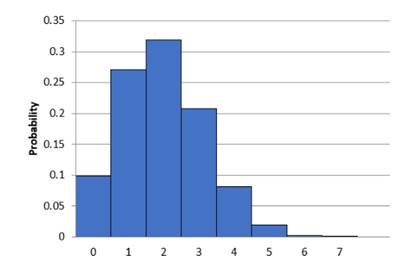
To make: a histogram for showing the probability distribution for X.
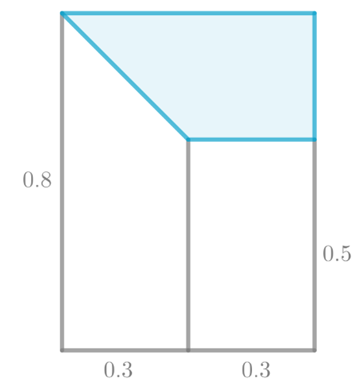
Given information:
An average of 7 gopher holes appears on the farm shown each week.
Concept Used:
Probability:
It is the ratio of number of ways it can happen to the total number of outcomes:
Binomial Experiment Probability:
The probability of k successes in the n trials for a binomial experiment is given by
Calculation:
From the previous part, the probabilities for the value of
From the previous part, the table for showing the probability distribution for X
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P(X) | 0.099 | 0.271 | 0.319 | 0.208 | 0.081 | 0.019 | 0.0025 | 0.0001 |
The histogram is shown below:
Chapter 6 Solutions
Holt Mcdougal Larson Algebra 2: Student Edition 2012
- Safari File Edit View History Bookmarks Window Help Ο Ω OV O mA 0 mW ర Fri Apr 4 1 222 tv A F9 F10 DII 4 F6 F7 F8 7 29 8 00 W E R T Y U S D பட 9 O G H J K E F11 + 11 F12 O P } [arrow_forwardSo confused. Step by step instructions pleasearrow_forwardIn simplest terms, Sketch the graph of the parabola. Then, determine its equation. opens downward, vertex is (- 4, 7), passes through point (0, - 39)arrow_forward
- In simplest way, For each quadratic relation, find the zeros and the maximum or minimum. a) y = x 2 + 16 x + 39 b) y = 5 x2 - 50 x - 120arrow_forwardIn simplest terms and step by step Write each quadratic relation in standard form, then fi nd the zeros. y = - 4( x + 6)2 + 36arrow_forwardIn simplest terms and step by step For each quadratic relation, find the zeros and the maximum or minimum. 1) y = - 2 x2 - 28 x + 64 2) y = 6 x2 + 36 x - 42arrow_forward
- Write each relation in standard form a)y = 5(x + 10)2 + 7 b)y = 9(x - 8)2 - 4arrow_forwardIn simplest form and step by step Write the quadratic relation in standard form, then fi nd the zeros. y = 3(x - 1)2 - 147arrow_forwardStep by step instructions The path of a soccer ball can be modelled by the relation h = - 0.1 d 2 + 0.5 d + 0.6, where h is the ball’s height and d is the horizontal distance from the kicker. a) Find the zeros of the relation.arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





