
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
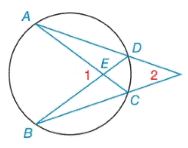
Chapter 6.2, Problem 10E
| Given: |
|
| Find: |
|
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
BH is tangent to circle A and DF is a diameter. I don't know where to go from here. May you help please?
find the area.
6 m
10 m
#
4 m
Chapter 6 Solutions
Elementary Geometry For College Students, 7e
Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - Given: AOOBandOCbisectsACBinO Find: a mAB b mACB c...Ch. 6.1 - Given: ST=12(SR)inQSRisadiameter Find: a mST b mTR...
Ch. 6.1 - Given: QinwhichmAB:mBC:mCA=2:3:4 Find: a mAB b mBC...Ch. 6.1 - Given: mDOE=76and mEOG=82inO EFisadiameter Find: a...Ch. 6.1 - Given: OwithABACand mBOC=72 Find: a mBC b mAB c mA...Ch. 6.1 - In O not shown, OA is a radius, AB is a diameter,...Ch. 6.1 - Given: In O,OCABand OC=6 Find: a AB b BC Exercise...Ch. 6.1 - Prob. 16ECh. 6.1 - Given: Concentric circles with center Q...Ch. 6.1 - AB is the common chord of O and Q. If AB=12 and...Ch. 6.1 - Circles O and Q have the common chord AB. If AB=6,...Ch. 6.1 - Suppose that a circle is divided into three...Ch. 6.1 - Suppose that a circle is divided by points A,B,C,...Ch. 6.1 - Prob. 22ECh. 6.1 - Prob. 23ECh. 6.1 - Prob. 24ECh. 6.1 - Prob. 25ECh. 6.1 - Five points are equally spaced on a circle. A...Ch. 6.1 - A ceiling fan has equally spaced blades. What is...Ch. 6.1 - A wheel has equally spaced lug bolts. What is the...Ch. 6.1 - An amusement park ride the Octopus has eight...Ch. 6.1 - In Exercises 30 and 31, complete each proof....Ch. 6.1 - Prob. 31ECh. 6.1 - In Exercises 32 to 37, write a paragraph proof....Ch. 6.1 - Prob. 33ECh. 6.1 - Prob. 34ECh. 6.1 - Prob. 35ECh. 6.1 - Prob. 36ECh. 6.1 - In Exercises 32 to 37, write a paragraph proof. If...Ch. 6.1 - If MNPQin O, explain why MNPQ is an isosceles...Ch. 6.1 - If STTV, explain why STV is an isosceles triangle.Ch. 6.1 - Prob. 40ECh. 6.1 - In O,OY=5 and XZ=6. If XWWY, find WZ.Ch. 6.2 - Given: mAB=92mDA=114mBC=138 Find:...Ch. 6.2 - Given: mDC=30 and mDABC is trisected at points A...Ch. 6.2 - Given: Circle O with diameter RS, tangent SW,...Ch. 6.2 - Prob. 4ECh. 6.2 - Prob. 5ECh. 6.2 - Is it possible for a a rectangle inscribed in a...Ch. 6.2 - Given: In Q, PR contains Q, MR is a tangent,...Ch. 6.2 - Given: AB and AC are tangent to O, mBC=126 Find:...Ch. 6.2 - Given: Tangent ABand AC to O mACB=68 Find:...Ch. 6.2 - Given: m1=72,mDC=34 Find: a)mABb)m2Ch. 6.2 - Given: m2=36mAB=4mDC Find: a)mABb)m1Ch. 6.2 - Given: m3=42 Find: a)mRTb)mRST Exercises 12,13Ch. 6.2 - Given: RSSTRT Find: a)mRTb)mRSTc)m3 Exercises...Ch. 6.2 - Given: m1=63mRS=3x+6mVT=x Find: mRS Exercises 14,...Ch. 6.2 - Given: m2=124mTV=x+1mSR=3(x+1) Find: mTV Exercises...Ch. 6.2 - Given: m1=71m2=33 Find: mCE and mBD Exercises 16,...Ch. 6.2 - Given: m1=62m2=26 Find: mCE and mBD Exercises 16,...Ch. 6.2 - aHow are R and T related? bFind mR if mT=112....Ch. 6.2 - Prob. 19ECh. 6.2 - A quadrilateral RSTV is circumscribed about a...Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - Prob. 23ECh. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - An airplane reaches an altitude of 3mi above the...Ch. 6.2 - From the veranda of a beachfront hotel, Manny is...Ch. 6.2 - For the five-pointed star a regular pentagram...Ch. 6.2 - For the six-pointed star a regular hexagram...Ch. 6.2 - A satellite dish in the shape of a regular...Ch. 6.2 - In the figure shown, RSTWVT by the reason AA. Name...Ch. 6.2 - In the figure shown, RXVWXS by the reason AA. Name...Ch. 6.2 - On a fitting for a hex wrench, the distance from...Ch. 6.2 - Given: AB is a diameter of M is the midpoint of...Ch. 6.2 - A surveyor sees a circular planetarium through an...Ch. 6.2 - The larger circle is inscribed in a square with...Ch. 6.2 - In R,QS=2(PT). Also, mP=23. Find mVRS.Ch. 6.2 - Prob. 39ECh. 6.2 - Prob. 40ECh. 6.2 - Prob. 41ECh. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - Prob. 43ECh. 6.2 - Prob. 44ECh. 6.2 - Prob. 45ECh. 6.2 - Prob. 46ECh. 6.2 - Prob. 47ECh. 6.2 - Given concentric circles with center O, ABC is...Ch. 6.2 - Prob. 49ECh. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Sketch two circles that have: a No common tangents...Ch. 6.3 - Two congruent intersecting circles B and D not...Ch. 6.3 - Prob. 7ECh. 6.3 - Prob. 8ECh. 6.3 - Prob. 9ECh. 6.3 - Prob. 10ECh. 6.3 - Prob. 11ECh. 6.3 - Prob. 12ECh. 6.3 - Prob. 13ECh. 6.3 - Prob. 14ECh. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - For Exercises 17 to 20. See Theorem 6.3.6. Given:...Ch. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - Prob. 19ECh. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - Prob. 21ECh. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - Prob. 24ECh. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - Prob. 28ECh. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - Prob. 30ECh. 6.3 - Does it follow from Exercise 30 that ADE is also...Ch. 6.3 - Prob. 32ECh. 6.3 - The cylindrical brush on a vacuum cleaner is...Ch. 6.3 - Prob. 34ECh. 6.3 - Given: Tangents AB,BC,andACtoO at points M, N, and...Ch. 6.3 - Given: Q is inscribed in isosceles right RST. The...Ch. 6.3 - Given: AB is an external tangent to O and Q at...Ch. 6.3 - Prob. 38ECh. 6.3 - The center of a circle of radius 2 in. is at a...Ch. 6.3 - Circles O, P, and Q are tangent as shown at points...Ch. 6.3 - Prob. 41ECh. 6.3 - Prob. 42ECh. 6.3 - Prob. 43ECh. 6.3 - If the larger gear has 30 teeth and smaller gear...Ch. 6.3 - Prob. 45ECh. 6.3 - In Exercises 46 to 49, prove the stated theorem....Ch. 6.3 - Prob. 47ECh. 6.3 - Prob. 48ECh. 6.3 - Prob. 49ECh. 6.3 - Prob. 50ECh. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - Prob. 2ECh. 6.4 - Prob. 3ECh. 6.4 - Prob. 4ECh. 6.4 - Prob. 5ECh. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - Prob. 8ECh. 6.4 - Prob. 9ECh. 6.4 - Prob. 10ECh. 6.4 - X, Y, and Z are on circle O such that mXY=120,...Ch. 6.4 - Prob. 12ECh. 6.4 - Construct the two tangent segments to circle P not...Ch. 6.4 - Construct the two tangent segments to circle R not...Ch. 6.4 - Point V is in the exterior of circle Q not shown...Ch. 6.4 - Prob. 16ECh. 6.4 - Prob. 17ECh. 6.4 - Prob. 18ECh. 6.4 - Prob. 19ECh. 6.4 - a If mRSmTV, write an inequality that compares m1...Ch. 6.4 - a If MNPQ, write an inequality that compares the...Ch. 6.4 - Prob. 22ECh. 6.4 - Quadrilateral ABCD is inscribed in circle P not...Ch. 6.4 - Quadrilateral RSTV is inscribed in circle Q not...Ch. 6.4 - In circle O, points A, B, and C are on the circle...Ch. 6.4 - Prob. 26ECh. 6.4 - Prob. 27ECh. 6.4 - Triangle ABC is inscribed in circle O; AB=5, BC=6,...Ch. 6.4 - Given circle O with mBC=120, and mAC=130. a Which...Ch. 6.4 - Given that mAC:mBC:mAB=4:3:2 in circle O: a Which...Ch. 6.4 - Prob. 31ECh. 6.4 - Circle O has a diameter of length 20cm. Chord AB...Ch. 6.4 - Prob. 33ECh. 6.4 - A tangent ET is constructed to circle Q from...Ch. 6.4 - Prob. 35ECh. 6.4 - Prob. 36ECh. 6.4 - Prob. 37ECh. 6.4 - Prove: In a circle containing two unequal chords,...Ch. 6.4 - In O, chord AB chord CD. Radius OE is...Ch. 6.4 - In P, whose radius has length 8in., mAB=mBC=60....Ch. 6.4 - Prob. 41ECh. 6.CR - The length of the radius of a circle is 15 mm. The...Ch. 6.CR - Find the length of a chord that is 8 cm from the...Ch. 6.CR - Two circles intersect and have a common chord 10...Ch. 6.CR - Two circles intersect and have a common chord 12...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - Prob. 6CRCh. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - Prob. 9CRCh. 6.CR - Prob. 10CRCh. 6.CR - Given:Owithtangentlandm1=46 Find:m2, m3,m4,m5Ch. 6.CR - Given:Owithtangentlandm5=40 Find:m1,m2, m3,m4,Ch. 6.CR - Two circles are concentric. A chord of the larger...Ch. 6.CR - Two parallel chords of a circle each have length...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - Prob. 20CRCh. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given:DF-AC-inO OE=5x+4 OB=2x+19 Find:OECh. 6.CR - Given:OE-OB-inO DF=xx-2 AC=x+28 Find:DEandACCh. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - Given:OwithdiameterAC-andtangentDE...Ch. 6.CR - A square is inscribed in a circle with a radius of...Ch. 6.CR - A 30-60-90 triangle is inscribed in a circle with...Ch. 6.CR - A circle is inscribed in the right triangle. The...Ch. 6.CR - Given:OisinscribedinABC AB=9,BC=13,AC=10...Ch. 6.CR - In Q with ABQ and CDQ, mABmCD. Also, QPABandQRCD....Ch. 6.CT - a If mAB=88, then mACB=____________. b If mAB=92...Ch. 6.CT - a If mBC=69, then mBOC=_____________. b If mBC=64,...Ch. 6.CT - a If mBAC=24, then mBC=_____________. b If ABAC,...Ch. 6.CT - Complete each theorem: a An angle inscribed in a...Ch. 6.CT - Given that mAB=106 and mDC=32, find: a m1 b m2Ch. 6.CT - Given the tangents with mRT=146, find : a mRST b...Ch. 6.CT - Given the tangents with m3=46, find: a mRST b mRTCh. 6.CT - aBecause point Q is their common center, these...Ch. 6.CT - In O with diameter AC, OC=5 and AB=6. If M is the...Ch. 6.CT - For the circles described and shown, how many...Ch. 6.CT - aIf HP=4, PJ=5, and PM=2, find LP. bIf HP=x+1,...Ch. 6.CT - In the figure, TV is a tangent and TVWTXV. Find TV...Ch. 6.CT - Construct the tangent line to P at point X.Ch. 6.CT - aIf mABmCD, write an inequality that compares...Ch. 6.CT - In P not shown, the length of radius PA is 5....Ch. 6.CT - Provide the missing statements and reasons in the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- 2arrow_forwardCan someone help me with this please?arrow_forwardMariela is in her classroom and looking out of a window at a tree, which is 20 feet away. Mariela’s line of sight to the top of the tree creates a 42° angle of elevation, and her line of sight to the base of the tree creates a 31° angle of depression. What is the height of the tree, rounded to the nearest foot? Be sure to show your work to explain how you got your answer.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
01 - Angles and Angle Measure in Degrees - Part 1 - Types of Angles & What is an Angle?; Author: Math and Science;https://www.youtube.com/watch?v=hy95VyPet-M;License: Standard YouTube License, CC-BY