
Concept explainers
Power and energy Power and energy are often used interchangeably, but they are quite different. Energy is what makes matter move or heat up and is measured in units of joules (J) or Calories (Cal), where 1 Cal = 4184 J. One hour of walking consumes roughly 106 J, or 250 Cal. On the other hand, power is the rate at which energy is used and is measured in watts (W; 1 W = 1 J/s). Other useful units of power are kilowatts (1 kW = 103 W) and megawatts (1 MW = 106 W). If energy is used at a rate of 1 kW for 1 hr, the total amount of energy used is 1 kilowatt-hour (kWh), which is 3.6 × 106 J.
Suppose the power function of a large city over a 24-hr period is given by
where P is measured in megawatts and t = 0 corresponds to 6:00 P.M. (see figure).
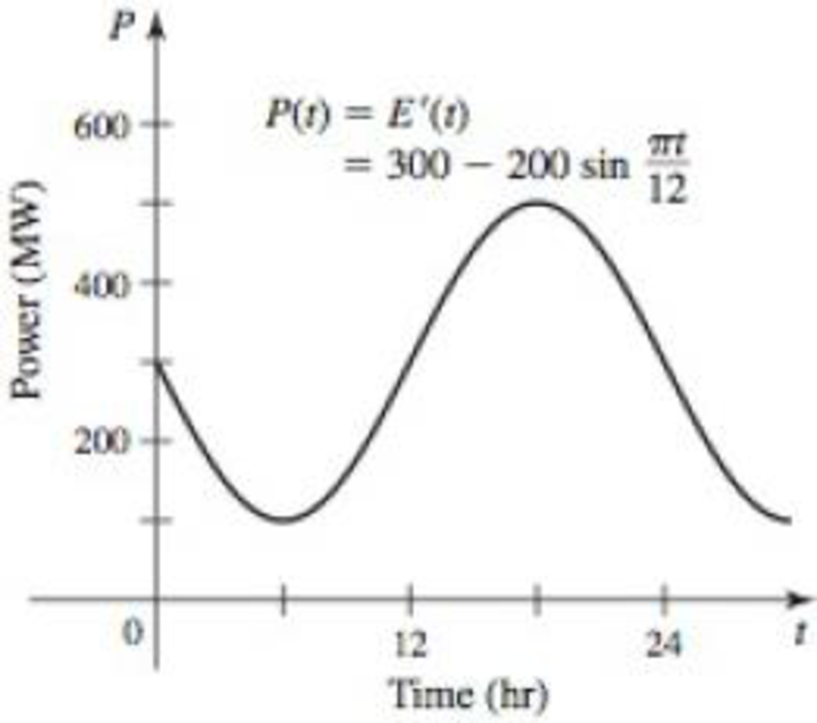
- a. How much energy is consumed by this city in a typical 24-hr period? Express the answer in megawatt-hours and in joules.
- b. Burning 1 kg of coal produces about 450 kWh of energy. How many kg of coal are required to meet the energy needs of the city for 1 day? For 1 year?
- c. Fission of 1 g of uranium-235 (U-235) produces about 16,000 kWh of energy. How many grams of uranium are needed to meet the energy needs of the city for 1 day? For 1 year?
- d. A typical wind turbine can generate electrical power at a rate of about 200 kW. Approximately how many wind turbines are needed to meet the average energy needs of the city?
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
Additional Math Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Algebra and Trigonometry (6th Edition)
Pre-Algebra Student Edition
Elementary Statistics (13th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- Let X be a discrete random variable taking values in {0, 1, 2, . . . }with the probability generating function G(s) = E(sX). Prove thatVar(X) = G′′(1) + G′(1) − [G′(1)]2.[5 Marks](ii) Let X be a random variable taking values in [0,∞) with proba-bility density functionfX(u) = (5/4(1 − u^4, 0 ≤ u ≤ 1,0, otherwise. Let y =x^1/2 find the probability density function of Yarrow_forward2. y 1 Ο 2 3 4 -1 Graph of f x+ The graph gives one cycle of a periodic function f in the xy-plane. Which of the following describes the behavior of f on the interval 39 x < 41 ? (Α B The function f is decreasing. The function f is increasing. The function f is decreasing, then increasing. D The function f is increasing, then decreasing.arrow_forwardDepth (feet) 5- 4- 3- 2. WW www 1 D B 0 10 20 30 40 50 60 70 80 Time (hours) x A graph of the depth of water at a pier in the ocean is given, along with five labeled points A, B, C, D, and E in the xy-plane. For the time periods near these data points, a periodic relationship between depth of water, in feet, and time, in hours, can be modeled using one cycle of the periodic relationship. Based on the graph, which of the following is true? B C The time interval between points A and B gives the period. The time interval between points A and C gives the period. The time interval between points A and D gives the period. The time interval between points A and E gives the period.arrow_forward
- A certain type of machine produces a number of amps of electricity that follows a cyclic, periodically increasing and decreasing pattern. The machine produces a maximum of 7 amps at certain times and a minimum of 2 amps at other times. It takes about 5 minutes for one cycle from 7 amps to the next 7 amps to occur. Which of the following graphs models amps as a function of time, in minutes, for this machine? A B C D Amps M 3 4 5 678 Minutes Amps w 3 4 5 6 7 8 Minutes 8 Amps- 6+ Amps y 2345678 Minutes 456 8 Minutesarrow_forward5 4. ·3. -2+ 1+ AN -5 -3 -4- 1 x 3 ད Graph of f The graph of the function f is given in the xy- plane. Which of the following functions has the same period as f? A B ми warrow_forwarda C d 2 1 -1 0 1 2 3 -1 Graph of f'(x) (5) The graph of f'(x), the derivative of f(x), is shown in the figure above. The line tangent to the graph of f'(x) at x=0 is vertical and f'(x) is not differentiable at x = 1. Which of the following statements is true? (a) f'(x) does not exist at x = 0. (b) f(x) has a point of inflection at x = 1. (c) f(x) has a local maximum at x = 0. (d) f(x) has a local maximum at x = 1.arrow_forward
- Let C be the intersection of the cylinder x² + y² = 2.95 with the plane z = 1.13x, with the clockwise orientation, as viewed from above. Then the value of COS (₤2 yo 2 y dx -x dy+3zdz is 0.131 -0.108 -0.891 -0.663 -0.428 0.561 -0.332 -0.387arrow_forwarduse a graphing utility to sketch the graph of the function and then use the graph to help identify or approximate the domain and range of the function. f(x)= x*sqrt(9-(x^2))arrow_forwarduse a graphing utility to sketch the graph of the function and then use the graph to help identify or approximate the domain and range of the function. f(x)=xsqrt(9-(x^2))arrow_forward
- Calculate a (bxc) where a = i, b = j, and c = k.arrow_forwardi+2j+3k = (1,2,3) and b = -i-k. Calculate the cross product a x b where a Next calculate the area of the parallelogram spanned by a and b.arrow_forwardThe measured receptance data around two resonant picks of a structure are tabulated in the followings. Find the natural frequencies, damping ratios, and mode shapes of the structure. (30 points) (@)×10 m/N α₁₂ (@)×10 m/N w/2z (Hz) 99 0.1176 0.17531 0.1114 -0.1751i 101 -0.0302 0.2456i -0.0365 -0.2453i 103 -0.1216 0.1327i -0.1279-0.1324i 220 0.0353 0.0260i -0.0419+0.0259i 224 0.0210 0.0757i |-0.0273 +0.0756i 228 -0.0443 0.0474i 0.0382 +0.0474iarrow_forward
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning





