
Concept explainers
The truss shown consists of six members and is supported by a short link at A. two short links at B, and a ball and socket at D. Determine the force in each of the members for the given loading.
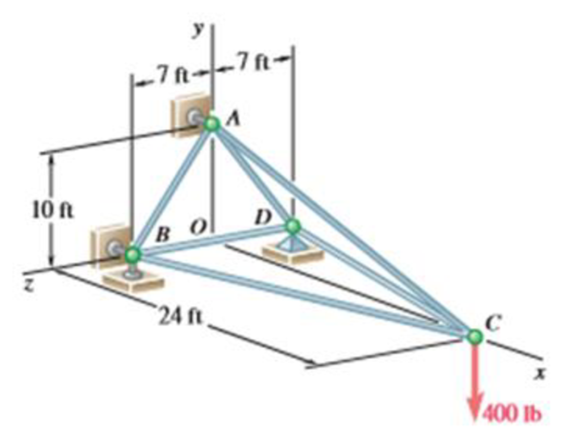
The force in each of the members of the truss for the given loading.
Answer to Problem 6.35P
The force in member AC is
Explanation of Solution
The free-body diagram of the entire truss is shown in figure 1.
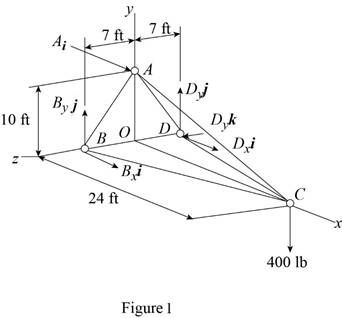
Refer to figure 1 and use symmetry.
Here,
Write the equilibrium equations taking the moments about
Here,
Write the equation for
Here,
Put the above equation in equation (II).
The
Here,
Write the expression for
Put the above equation in equation (III).
Put equation (I) in the above equation.
Substitute
The
Here,
Write the expression for
Put the above equation in equation (IV).
Put equation (I) in the above equation.
Write the expression for the reaction at the point B.
Here
Substitute
Consider the free-body joint C. The free-body diagram of joint C is shown in figure 2.
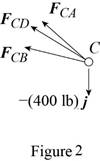
Refer to figure (2) and write the expression for the forces.
Here,
Write the expression for
Find the magnitude of
Substitute
Write the expression for
Here,
Substitute
Write the expression for
Here,
Substitute
The net force must be equal to zero.
Here,
Write the expression for
Put the above equation in equation (IX).
Put equations (VI), (VII) and (VIII) in the above equation.
Equate the coefficient of
Equate the coefficient of
Equate the coefficient of
Put the above equation in equation (XI).
Substitute
Consider the free-body joint B. The free-body diagram of joint B is shown in figure 3.
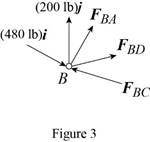
Refer to figure (3) and write the expression for the forces.
Here,
Substitute
Write the expression for
Here,
Substitute
Write the expression for
Here,
Write the expression for
Put the above equation in equation (IX).
Put equations (XIV), (XV) and (XVI) in the above equation.
Substitute
Equate the coefficient of
Equate the coefficient of
Substitute
From symmetry,
Here,
Substitute
Conclusion:
Thus, the force in member AC is
Want to see more full solutions like this?
Chapter 6 Solutions
EBK VECTOR MECHANICS FOR ENGINEERS: STA
- 3. Given the truss shown below, determine the force in members CD, CE, BE, CB and AB and state whether the members are in tension or compression. 500 Ib 500 lb - 3 ft-3 ft- -3 ft- 6 ft 800 lb BO 6 ft A -9 ftarrow_forwardThe Howe bridge truss is subjected to the loading shown. Determine the force in members HI,HB, and BC, and state if the members are in tension or compressionarrow_forwardDetermine (approximately) the forces in each truss member and column of the portal frame. Assume all members of the truss and columns to be pin connected at their ends. (Provide complete solution, summary of results) 6 ft F 6 ft 4k D E H 3 ft 12 ft Font sa- -8 ft-8 ft--8 ft--8 ft-arrow_forward
- Solve the following problems by the method of sections. State whether the members are in tension or compression. Determine the forces in members BC, BF, and EF of the truss shown in Fig. B 4 m E F G 3 m -3 m 3 m 5 kN 3 kNarrow_forwardTwo members, each consisting of straight and 168-mm radius quarter-circle, are connected as shown and support a 500-N load at D. Draw the FBD of the entire frame and members ABC and DBC, including dimensions. Determine the forces in member ABC. Also, calculate the force exerted by member DBC on pin C.arrow_forward(b) Figure Q1(b) demonstrates a truss system applied with several forces at points B, E and H. If the values of F = 25 kN and L = 2.5 m, determine the axial forces in members BE and DG using the Method of Sections. D. I A B E H 'F 2F F Figure Q1 (b)arrow_forward
- Calculate the forces in members BE and BD of the loaded truss. The forces are positive if in tension, negative if in compression. Assume F = 4.4 kN, a = 2.9 m, b = 3 m, c = 2 m, and d = 2 m. A F Answers: BE = BD = a i B b E a b D d kN kNarrow_forwardThe truss is supported by a pin connection at A and a roller at E. It is loaded as shown. Use the picture below to determine the forces in members CD, CF, GF. Enter each value in separate questions and report all answers in kN but do not enter units. Report positive values for members in tension and negative values for members in compression. Determine the force in CD, CF and GF with appropriate units. Thanks.arrow_forwardQ3) Determine the force in member BC, BD and BE of the truss shown in the figure and specify whether force is in tension or compression. 148 KN 4 m- B diye C -4 m---4 m-4 D F E H 4.5 marrow_forward
- 3. The planar truss below is supported by a pin joint at G and a roller at E. Determine the forces in members AB and AF using Method of Joints (MOJ). Determine the forces in members CD, CE, and EF using Method of Sections (MOS). State whether each member is in tension (T) or compression (C). Please put your final answers in the table provided. 2 m A G 2 m B F 2 m 3 kN E -2 m- D. 2 kN 3 m Member AB AF CD CE EF Force (kN) T/Carrow_forwardCalculate the forces in members BE and BD of the loaded truss. The forces are positive if in tension, negative if in compression. Assume F = 6.2 kN, a = 3.4 m, b = 3 m, c = 2 m, and d = 2 m. b b A F Answers: BE = BD = a i IN E a D KN kNarrow_forwardProblem 1 For the frame loaded as shown, determine all the forces on members AD and ABC. Support at C is a roller. Hint: Please be careful in this problem: at point A, there are three elements connected at A: a pin A that is connected to ground (so, two support reactions due to that, say Ax and Ay), then, bar AD (two more reactions at A due to bar AD: call these as Ax_prime, and Ay_prime) and the bar AC (two more reactions at A due to bar AC: call these as Ax_doubleprime, Ay_doubleprime). So, you will need to draw a pin FBD at A showing all the six forces. 200 N 130 mm 400 mm V400 N A B -400 mm 400 mmarrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
