
Concept explainers
Matching In Exercises 57–-60, match the
are labeled (a), (b), (c), and (d).]
a). 
b). 
c). 
d). 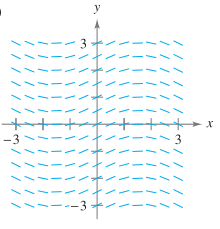
Trending nowThis is a popular solution!

Chapter 6 Solutions
Bundle: Calculus: Early Transcendental Functions, 7th + Webassign, Multi-term Printed Access Card
- Question Find the following limit. Select the correct answer below: 1 2 0 4 5x lim sin (2x)+tan 2 x→arrow_forward12. [0/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.022. Evaluate the indefinite integral. (Use C for the constant of integration.) sin(In 33x) dxarrow_forward2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.003.MI. Evaluate the integral by making the given substitution. (Use C for the constant of integration.) x³ + 3 dx, u = x² + 3 Need Help? Read It Watch It Master It SUBMIT ANSWER 3. [-/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.006.MI. Evaluate the integral by making the given substitution. (Use C for the constant of integration.) | +8 sec² (1/x³) dx, u = 1/x7 Need Help? Read It Master It SUBMIT ANSWER 4. [-/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.007.MI. Evaluate the indefinite integral. (Use C for the constant of integration.) √x27 sin(x28) dxarrow_forward
- 53,85÷1,5=arrow_forward3. In the space below, describe in what ways the function f(x) = -2√x - 3 has been transformed from the basic function √x. The graph f(x) on the coordinate plane at right. (4 points) -4 -&- -3 -- -2 4 3- 2 1- 1 0 1 2 -N -1- -2- -3- -4- 3 ++ 4arrow_forward2. Suppose the graph below left is the function f(x). In the space below, describe what transformations are occuring in the transformed function 3ƒ(-2x) + 1. The graph it on the coordinate plane below right. (4 points)arrow_forward
- 1 1. Suppose we have the function f(x) = = and then we transform it by moving it four units to the right and six units down, reflecting it horizontally, and stretching vertically by 5 units. What will the formula of our new function g(x) be? (2 points) g(x) =arrow_forwardSuppose an oil spill covers a circular area and the radius, r, increases according to the graph shown below where t represents the number of minutes since the spill was first observed. Radius (feet) 80 70 60 50 40 30 20 10 0 r 0 10 20 30 40 50 60 70 80 90 Time (minutes) (a) How large is the circular area of the spill 30 minutes after it was first observed? Give your answer in terms of π. square feet (b) If the cost to clean the oil spill is proportional to the square of the diameter of the spill, express the cost, C, as a function of the radius of the spill, r. Use a lower case k as the proportionality constant. C(r) = (c) Which of the following expressions could be used to represent the amount of time it took for the radius of the spill to increase from 20 feet to 60 feet? r(60) - r(20) Or¹(80-30) r(80) - r(30) r-1(80) - r−1(30) r-1(60) - r¹(20)arrow_forward6. Graph the function f(x)=log3x. Label three points on the graph (one should be the intercept) with corresponding ordered pairs and label the asymptote with its equation. Write the domain and range of the function in interval notation. Make your graph big enough to see all important features.arrow_forward
- Find the average value gave of the function g on the given interval. gave = g(x) = 8√√x, [8,64] Need Help? Read It Watch Itarrow_forward3. Mary needs to choose between two investments: One pays 5% compounded annually, and the other pays 4.9% compounded monthly. If she plans to invest $22,000 for 3 years, which investment should she choose? How much extra interest will she earn by making the better choice? For all word problems, your solution must be presented in a sentence in the context of the problem.arrow_forward4 πT14 Sin (X) 3 Sin(2x) e dx 1716 S (sinx + cosx) dxarrow_forward
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
