C++ for Engineers and Scientists
4th Edition
ISBN: 9781133187844
Author: Bronson, Gary J.
Publisher: Course Technology Ptr
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.1, Problem 4E
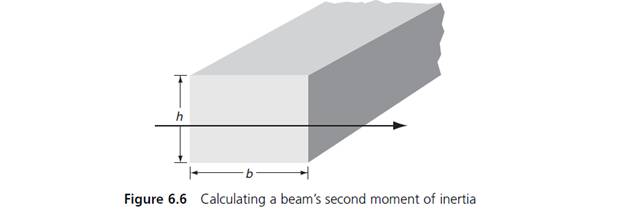
(Statics) A beam’s second moment of inertia, also known as its area moment of inertia, is used to determine its resistance to bending and deflection. For a rectangular beam (see Figure 6.6), the second moment of inertia is given by this formula:
I is the second moment of inertia (m4).
b is the base (m).
h is the height (m).
a. Using this formula, write a function called beamMoment() that accepts two double- precision numbers as parameters (one for the base and one for the height), calculates the corresponding second moment of inertia, and displays the result.
b. Include the function written in Exercise 4a in a working
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please original work
What are four of the goals of information lifecycle management think they are most important to data warehousing,
Why do you feel this way, how dashboards can be used in the process, and provide a real life example for each.
Please cite in text references and add weblinks
The following is code for a disc golf program written in C++:
// player.h
#ifndef PLAYER_H
#define PLAYER_H
#include <string>
#include <iostream>
class Player {
private:
std::string courses[20]; // Array of course names
int scores[20]; // Array of scores
int gameCount; // Number of games played
public:
Player(); // Constructor
void CheckGame(int playerId, const std::string& courseName, int gameScore);
void ReportPlayer(int playerId) const;
};
#endif // PLAYER_H
// player.cpp
#include "player.h"
#include <iomanip>
Player::Player() : gameCount(0) {}
void Player::CheckGame(int playerId, const std::string& courseName, int gameScore) {
for (int i = 0; i < gameCount; ++i) {
if (courses[i] == courseName) {
// If course has been played, then check for minimum score
if (gameScore < scores[i]) {
scores[i] = gameScore; // Update to new minimum…
In this assignment, you will implement a multi-threaded program (using C/C++) that will
check for Prime Numbers and Palindrome Numbers in a range of numbers. Palindrome
numbers are numbers that their decimal representation can be read from left to right and
from right to left (e.g. 12321, 5995, 1234321).
The program will create T worker threads to check for prime and palindrome numbers in the
given range (T will be passed to the program with the Linux command line). Each of the
threads works on a part of the numbers within the range.
Your program should have some global shared variables:
•
numOfPrimes: which will track the total number of prime numbers found by all
threads.
numOfPalindroms: which will track the total number of palindrome numbers found
by all threads.
numOfPalindromic Primes: which will count the numbers that are BOTH prime and
palindrome found by all threads.
TotalNums: which will count all the processed numbers in the range.
In addition, you need to have arrays…
Chapter 6 Solutions
C++ for Engineers and Scientists
Ch. 6.1 - (Practice) For the following function headers,...Ch. 6.1 - Prob. 2ECh. 6.1 - Prob. 3ECh. 6.1 - (Statics) A beam’s second moment of inertia, also...Ch. 6.1 - (Statics) An annulus is a cylindrical rod with a...Ch. 6.1 - Prob. 6ECh. 6.1 - (Physics) Buoyancy is the upward force a liquid...Ch. 6.1 - (Numerical) a. Write a C++ program that accepts an...Ch. 6.1 - (Practice) a. Write a function that produces a...Ch. 6.1 - Prob. 10E
Ch. 6.1 - Prob. 11ECh. 6.1 - Prob. 12ECh. 6.1 - Prob. 13ECh. 6.1 - Prob. 14ECh. 6.1 - Prob. 15ECh. 6.2 - Prob. 1ECh. 6.2 - (Practice) For the following function headers,...Ch. 6.2 - (General math) a. Write a function named...Ch. 6.2 - (General math) a. The volume, V, of a cylinder is...Ch. 6.2 - Prob. 6ECh. 6.2 - Prob. 10ECh. 6.2 - (Numerical) a. The following is an extremely...Ch. 6.2 - Prob. 12ECh. 6.2 - Prob. 13ECh. 6.3 - Prob. 2ECh. 6.3 - Prob. 4ECh. 6.3 - Prob. 5ECh. 6.4 - (Practice) The volume, v, and side surface area,...Ch. 6.4 - (Practice) Write a C++ program that accepts the...Ch. 6.4 - (Simulation) Write a program to simulate the roll...Ch. 6.4 - (Numerical) Write a program that tests the...Ch. 6 - Prob. 1PPCh. 6 - Prob. 2PPCh. 6 - Prob. 6PPCh. 6 - (Numerical) Heron’s formula for the area, A, of a...Ch. 6 - Prob. 10PP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- How do you distinguish between hardware and a software problem? Discuss theprocedure for troubleshooting any hardware or software problem. give one reference with your answer.arrow_forwardYou are asked to explain what a computer virus is and if it can affect computer’shardware or software. How do you protect your computer against virus? give one reference with your answer.arrow_forwardDistributed Systems: Consistency Models fer to page 45 for problems on data consistency. structions: Compare different consistency models (e.g., strong, eventual, causal) for distributed databases. Evaluate the trade-offs between availability and consistency in a given use case. Propose the most appropriate model for the scenario and explain your reasoning. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]arrow_forward
- Operating Systems: Deadlock Detection fer to page 25 for problems on deadlock concepts. structions: • Given a system resource allocation graph, determine if a deadlock exists. If a deadlock exists, identify the processes and resources involved. Suggest strategies to prevent or resolve the deadlock and explain their trade-offs. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardArtificial Intelligence: Heuristic Evaluation fer to page 55 for problems on Al search algorithms. tructions: Given a search problem, propose and evaluate a heuristic function. Compare its performance to other heuristics based on search cost and solution quality. Justify why the chosen heuristic is admissible and/or consistent. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 75 for graph-related problems. Instructions: • Implement a greedy graph coloring algorithm for the given graph. • Demonstrate the steps to assign colors while minimizing the chromatic number. • Analyze the time complexity and limitations of the approach. Link [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 150 for problems on socket programming. Instructions: • Develop a client-server application using sockets to exchange messages. • Implement both TCP and UDP communication and highlight their differences. • Test the program under different network conditions and analyze results. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 80 for problems on white-box testing. Instructions: • Perform control flow testing for the given program, drawing the control flow graph (CFG). • Design test cases to achieve statement, branch, and path coverage. • Justify the adequacy of your test cases using the CFG. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 10 for problems on parsing. Instructions: • Design a top-down parser for the given grammar (e.g., recursive descent or LL(1)). • Compute the FIRST and FOLLOW sets and construct the parsing table if applicable. • Parse a sample input string and explain the derivation step-by-step. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 20 for problems related to finite automata. Instructions: • Design a deterministic finite automaton (DFA) or nondeterministic finite automaton (NFA) for the given language. • Minimize the DFA and show all steps, including state merging. • Verify that the automaton accepts the correct language by testing with sample strings. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 60 for solving the Knapsack problem using dynamic programming. Instructions: • Implement the dynamic programming approach for the 0/1 Knapsack problem. Clearly define the recurrence relation and show the construction of the DP table. Verify your solution by tracing the selected items for a given weight limit. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 70 for problems related to process synchronization. Instructions: • • Solve a synchronization problem using semaphores or monitors (e.g., Producer-Consumer, Readers-Writers). Write pseudocode for the solution and explain the critical section management. • Ensure the solution avoids deadlock and starvation. Test with an example scenario. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr
Boolean Algebra - Digital Logic and Logic Families - Industrial Electronics; Author: Ekeeda;https://www.youtube.com/watch?v=u7XnJos-_Hs;License: Standard YouTube License, CC-BY
Boolean Algebra 1 – The Laws of Boolean Algebra; Author: Computer Science;https://www.youtube.com/watch?v=EPJf4owqwdA;License: Standard Youtube License