
Concept explainers
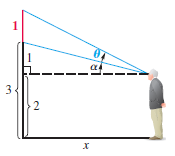
Observation of a Painting A painting 1 m high and 3 m from the floor will cut off an
assuming that the observer is x meters from the wall where the painting is displayed and that the eyes of the observer are 2 m above the ground. (See the figure.) Find the value of θ for the following values of x. Round to the nearest degree.
(a) 1 (b) 2 (c) 3
(d) Derive the formula given above. (Hint: Use the identity for tan(θ + α). Use right
(e) Graph the
(f) The concept in part (c) was first investigated in 1471 by the astronomer Regiomontanus. (Source: Maor, E., Trigonometric Delights. Princeton University Press.) If the bottom of the picture is a meters above eye level and the lop of the picture is b meters above eye level, then the optimum value of x is √ab meters. Use this result to find the exact answer to part (e).
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
MyLab Math with Pearson eText -- 24-Month Standalone Access Card -- for Trigonometry
- skip A swimming pool plan has concrete stairs leading down into the shallow end How much concrete will be needed to build the stairs? Bift 9 ft 2 ft 1 ft 9 ft 2 ft 5 ft [ ? ] ft³arrow_forwardFor the given right triangle, the longer leg is 8 units long and the shorter leg is 6 units long. sina=arrow_forwardWrite the equation of the trigonometric function shown in the graph. LO 5 4 3 2 1 y -5 -5 4 8 8 500 -1 -2 -3 -4 -5 x 5 15л 5л 25л 15л 35π 5л 4 8 2 8 4 8arrow_forward
- 2. If log2 (sin x) + log₂ (cos x) = -2 and log2 (sin x + cos x) = (-2 + log2 n), find n.arrow_forwardIf cscx- cotx = -4, find cscx + cotx.arrow_forwardQuestion 10 (5 points) (07.04 MC) Vectors u and v are shown in the graph. -12-11 -10 -9 -8 -7 -6 -5 What is proju? a -6.5i - 4.55j b -5.2i+2.6j с -4.7631 3.334j d -3.81i+1.905j < + 10 6 5 4 3 2 -3 -2 -10 1 -1 -2 -3 u -4 -5 -6 -7arrow_forward
- Find the lengths of PR and OR in terms of the angles α and β. Find the angles ∠ONQ and ∠NPQ. Find the lengths of ON and PN in terms of the angle β. Find the length of PQ. Find the length of QR. Find the length of OM. Find the length of RM. What formula can you write down by noting that PR = QR + PQ? What formula can you write down by noting that OR = OM - RM?arrow_forward5) Solve the triangle. 2 95° 4 B с A) c=3.63, A=59.5°, B = 25.5° C) c = 4.63, A = 59.5°, B = 25.5° A B) c 4.63, A 25.5°, B = 59.5° = = D) c 5.63, A = 25.5°, B = 59.5°arrow_forwardFind zw. Leave your answer in polar form. = လ 3π 2 z = 6 cos 6 cos 37 3π + i sin 2 57 W = 12 cos + i sin 6 6 ༠།ལྦ་arrow_forward
- 10 Write the expression (1 – i) i)in the standard form a + bi.arrow_forward11) The letters r and 0 represent polar coordinates. Write the equation r sine = 10 using rectangular coordinates (x, y). A) x = 10y B) y = 10 C) x = 10 D) y = 10xarrow_forward18) Find all the complex cube roots of - 8i. Leave your answers in polar form with the argument in degrees.arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning





