Chapter 6, Problem 8E

FILE The Downtown Parking Authority of Tampa, Florida, reported the following information for a sample of 250 customers on the number of hours cars are parked and the amount they are charged.

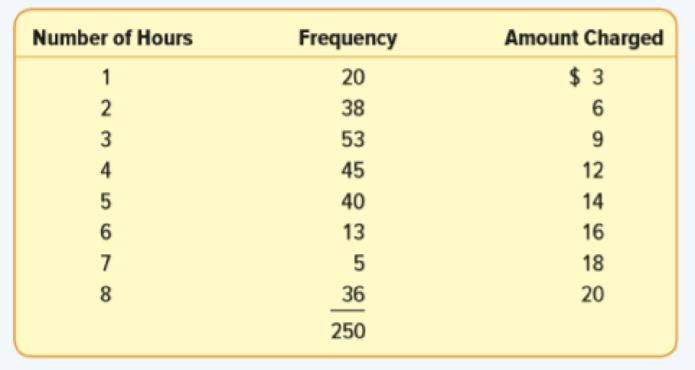
1. a. Convert the information on the number of hours parked to a probability distribution. Is this a discrete or a continuous probability distribution?
2. b. Find the mean and the standard deviation of the number of hours parked. How would you answer the question: How long is a typical customer parked?
3. c. Find the mean and the standard deviation of the amount charged.

To determine

Convert the number of hours parked to a probability distribution.

Identify whether this is a discrete or continuous probability distribution.

Answer to Problem 8E

The probability distribution of number of hours parked is as follows:

Number of hours	Probability
1	0.08
2	0.152
3	0.212
4	0.18
5	0.16
6	0.052
7	0.02
8	0.144

This is a discrete random variable.

Explanation of Solution

Probability distribution:

The possible outcomes of an experiment and the probability associated with each of its outcome is called probability distribution.

The probability distribution of the number of hours parked is calculated as follows.

Number of hours	Frequency	Amount charged	Probability
1	20	3	$\frac{20}{250}=0.08$
2	38	6	$\frac{38}{250}=0.152$
3	53	9	$\frac{53}{250}=0.212$
4	45	12	$\frac{45}{250}=0.18$
5	40	14	$\frac{40}{250}=0.16$
6	13	16	$\frac{13}{250}=0.052$
7	5	18	$\frac{5}{250}=0.02$
8	36	20	$\frac{36}{250}=0.144$
Total	250		1

Here, the random variable is the number of hours parked, which takes only a certain number of separated values. Hence, it is a discrete random variable.

To determine

Find the mean and standard deviation of the number of hours parked.

Explain the duration of a typical customer parked.

Answer to Problem 8E

The mean of the number of hours parked is 4.144.

The standard deviation of the number of hours parked is 2.0908.

A typical customer parked for 4.144 hours.

Explanation of Solution

The mean number of hours parked is calculated as follows:

$\begin{array}{c}\mu ={\displaystyle \sum xP\left(x\right)}\\ =\left(1\times 0.08\right)+\left(2\times 0.152\right)+\left(3\times 0.212\right)+\left(4\times 0.18\right)+\left(5\times 0.16\right)+\left(6\times 0.052\right)+\left(7\times 0.02\right)+\left(8\times 0.144\right)\\ =0.08+0.304+0.636+0.72+0.8+0.312+0.14+1.152\\ =4.144\end{array}$

Therefore, the mean number of hours parked is 4.144.

The standard deviation of the number of hours parked is calculated as follows:

$\begin{array}{c}\sigma =\sqrt{{\sigma }^2}\\ \sigma =\sqrt{{\displaystyle \sum \left[{\left(x-\mu \right)}^{2}P\left(x\right)\right]}}\\ =\sqrt{\begin{array}{l}\left[{\left(1-4.144\right)}^2\left(0.08\right)\right]+\left[{\left(2-4.144\right)}^2\left(0.152\right)\right]+\left[{\left(3-4.144\right)}^2\left(0.212\right)\right]+\\ \left[{\left(4-4.144\right)}^2\left(0.18\right)\right]+\left[{\left(5-4.144\right)}^2\left(0.16\right)\right]+\left[{\left(6-4.144\right)}^2\left(0.052\right)\right]+\\ \left[{\left(7-4.144\right)}^2\left(0.02\right)\right]+\left[{\left(8-4.144\right)}^2\left(0.144\right)\right]\end{array}}\\ =\sqrt{\begin{array}{l}\left(9.88\times 0.08\right)+\left(4.6\times 0.152\right)+\left(1.31\times 0.212\right)+\left(0.02\times 0.18\right)+\\ \left(0.73\times 0.16\right)+\left(3.44\times 0.052\right)+\left(8.16\times 0.02\right)+\left(14.87\times 0.144\right)\end{array}}\\ =\sqrt{0.79+0.7+0.28+0.00+0.12+0.18+0.16+2.14}\\ =\sqrt{4.3713}\\ =2.0908\end{array}$

Therefore, the standard deviation of the number of hours parked is 2.0908.

The typical value that is used to represent the central location of probability distribution is the mean. Therefore, the typical customer parked is 4.144 hours.

To determine

Calculate the mean and the standard deviation of the amount charged.

Answer to Problem 8E

The mean of the amount charged is 11.532.

The standard deviation of the amount charged is 5.0049.

Explanation of Solution

Mean:

The central location of probability distribution is called mean. It is also called as expected value. The mean of a discrete probability distribution is a weighted average in which the possible random variables are weighted by its corresponding probability values. It is denoted as $\mu$.

Variance:

The variance describes the amount of spread in a probability distribution. It is denoted as ${\sigma }^2$. The square root of the variance is the standard deviation.

The mean of the amount charged is calculated as follows:

$\begin{array}{c}\mu ={\displaystyle \sum xP\left(x\right)}\\ =\left\{\begin{array}{c}\left(3\times 0.08\right)+\left(6\times 0.152\right)+\left(9\times 0.212\right)+\left(12\times 0.18\right)+\\ \left(14\times 0.16\right)+\left(16\times 0.052\right)+\left(18\times 0.02\right)+\left(20\times 0.144\right)\end{array}\right\}\\ =0.24+0.912+1.908+2.16+2.24+0.832+0.36+2.88\\ =11.532\end{array}$

Therefore, the mean of the amount charged is 11.532.

The standard deviation of the amount charged is calculated as follows:

$\begin{array}{c}\sigma =\sqrt{{\sigma }^2}\\ \sigma =\sqrt{{\displaystyle \sum \left[{\left(x-\mu \right)}^{2}P\left(x\right)\right]}}\\ =\sqrt{\begin{array}{l}\left[{\left(3-11.532\right)}^2\left(0.08\right)\right]+\left[{\left(6-11.532\right)}^2\left(0.152\right)\right]+\left[{\left(9-11.532\right)}^2\left(0.212\right)\right]+\\ \left[{\left(12-11.532\right)}^2\left(0.18\right)\right]+\left[{\left(14-11.532\right)}^2\left(0.16\right)\right]+\left[{\left(16-11.532\right)}^2\left(0.052\right)\right]+\\ \left[{\left(18-11.532\right)}^2\left(0.02\right)\right]+\left[{\left(20-4.144\right)}^2\left(0.144\right)\right]\end{array}}\\ =\sqrt{\begin{array}{l}\left(72.80\times 0.08\right)+\left(30.6\times 0.152\right)+\left(6.41\times 0.212\right)+\left(0.22\times 0.18\right)+\\ \left(6.09\times 0.16\right)+\left(19.96\times 0.052\right)+\left(41.84\times 0.02\right)+\left(71.71\times 0.144\right)\end{array}}\\ =\sqrt{5.82+4.65+1.36+0.04+0.97+1.04+0.84+10.33}\\ =\sqrt{25.0490}\\ =5.0049\end{array}$

Therefore, the standard deviation of the amount charged is 5.0049.