
Concept explainers
a.
Construct the
Calculate the mean and standard deviation of this distribution.
a.
Answer to Problem 70DA
The probability distributions for the number of bedrooms are as follows:
| Number of Bedrooms | Frequency |
Probability |
| 2 | 24 | 0.2286 |
| 3 | 26 | 0.2476 |
| 4 | 26 | 0.2476 |
| 5 | 11 | 0.1048 |
| 6 | 14 | 0.1333 |
| 7 | 2 | 0.0190 |
| 8 | 2 | 0.0190 |
| Total | 105 | 1 |
The mean of the distribution is 3.8.
The standard deviation of the distribution is 1.4954.
Explanation of Solution
Step-by-step procedure to obtain the frequency table for bedrooms using EXCEL:
- Enter the data in an EXCEL sheet.
- Go to Insert > PivotTable > PivotTable.
- In Table/
Range , select the column Bedrooms and click OK. - In PivotTable Field List, drag Bedrooms to Row Labels and to ∑ values.
- Click on it from ∑ values.
- Choose Value Field Settings.
- In Summarize value field by, choose Count and click OK.
The output obtained is as follows:

The probability distributions for the number of bedrooms are calculated as follows:
| Number of Bedrooms | Frequency |
Probability |
| 2 | 24 | |
| 3 | 26 | |
| 4 | 26 | |
| 5 | 11 | |
| 6 | 14 | |
| 7 | 2 | |
| 8 | 2 | |
| Total | 105 | 1 |
The mean of the distribution is calculated as follows:
Therefore, the mean of the distribution is 3.8.
Consider the following table that shows preliminary calculations to compute the standard deviation:
| Bedrooms | Frequency |
Probability | ||
| 2 | 24 | 0.2286 | ||
| 3 | 26 | 0.2476 | ||
| 4 | 26 | 0.2476 | ||
| 5 | 11 | 0.1048 | ||
| 6 | 14 | 0.1333 | ||
| 7 | 2 | 0.0190 | ||
| 8 | 2 | 0.0190 | ||
| 105 | 2.2362 |
The standard deviation of the distribution is calculated as follows:
Therefore, the standard deviation of the distribution is 1.4954.
b.
Construct the probability distribution for the number of bathrooms.
Find the mean and standard deviation for this distribution.
b.
Answer to Problem 70DA
The probability distributions for the number of bathrooms are as follows:
| Number of Bathrooms | Frequency |
Probability |
| 1.5 | 24 | 0.2286 |
| 2 | 17 | 0.1619 |
| 2.5 | 13 | 0.1238 |
| 3 | 22 | 0.2095 |
| 3.5 | 11 | 0.1048 |
| 4 | 11 | 0.1048 |
| 4.5 | 3 | 0.0286 |
| 5 | 2 | 0.0190 |
| 5.5 | 2 | 0.0190 |
| 105 |
The mean of the distribution is 2.7189.
The standard deviation of the distribution is 1.0093.
Explanation of Solution
Step-by-step procedure to obtain the frequency table for bedrooms using EXCEL:
- Enter the data in an EXCEL sheet.
- Go to Insert > PivotTable > PivotTable.
- In Table/Range, select the column Bathrooms and click OK.
- In PivotTable Field List, drag Bathrooms to Row Labels and to ∑ values.
- Click on it from ∑ values.
- Choose Value Field Settings.
- In Summarize value field by, choose Count and click OK.
The output obtained is as follows:
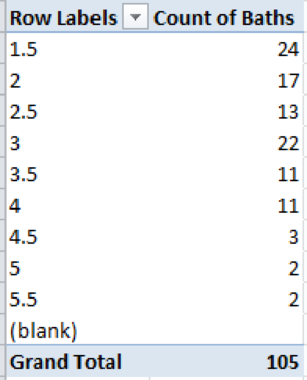
The probability distributions for the number of bathrooms are calculated as follows:
| Number of Bathrooms | Frequency |
Probability |
| 1.5 | 24 | |
| 2 | 17 | |
| 2.5 | 13 | |
| 3 | 22 | |
| 3.5 | 11 | |
| 4 | 11 | |
| 4.5 | 3 | |
| 5 | 2 | |
| 5.5 | 2 | |
| Total | 105 | 1 |
The mean of the distribution is calculated as follows:
Therefore, the mean of the distribution is 2.7189.
Consider the following table that shows preliminary calculations to compute the standard deviation:
| Number of Bathrooms | Frequency |
Probability | ||
| 1.5 | 24 | 0.2286 | ||
| 2 | 17 | 0.1619 | ||
| 2.5 | 13 | 0.1238 | ||
| 3 | 22 | 0.2095 | ||
| 3.5 | 11 | 0.1048 | ||
| 4 | 11 | 0.1048 | ||
| 4.5 | 3 | 0.0286 | ||
| 5 | 2 | 0.0190 | ||
| 5.5 | 2 | 0.0190 | ||
| Total | 105 |
The standard deviation of the distribution is calculated as follows:
Therefore, the standard deviation of the distribution is 1.0093.
Want to see more full solutions like this?
Chapter 6 Solutions
Loose Leaf for Statistical Techniques in Business and Economics
- Given your fitted regression line, what would be the residual for snake #5 (10 C)?arrow_forwardCalculate the 95% confidence interval around your estimate of r using Fisher’s z-transformation. In your final answer, make sure to back-transform to the original units.arrow_forwardCalculate Pearson’s correlation coefficient (r) between temperature and heart rate.arrow_forward
- A researcher wishes to estimate, with 90% confidence, the population proportion of adults who support labeling legislation for genetically modified organisms (GMOs). Her estimate must be accurate within 4% of the true proportion. (a) No preliminary estimate is available. Find the minimum sample size needed. (b) Find the minimum sample size needed, using a prior study that found that 65% of the respondents said they support labeling legislation for GMOs. (c) Compare the results from parts (a) and (b). ... (a) What is the minimum sample size needed assuming that no prior information is available? n = (Round up to the nearest whole number as needed.)arrow_forwardThe table available below shows the costs per mile (in cents) for a sample of automobiles. At a = 0.05, can you conclude that at least one mean cost per mile is different from the others? Click on the icon to view the data table. Let Hss, HMS, HLS, Hsuv and Hмy represent the mean costs per mile for small sedans, medium sedans, large sedans, SUV 4WDs, and minivans respectively. What are the hypotheses for this test? OA. Ho: Not all the means are equal. Ha Hss HMS HLS HSUV HMV B. Ho Hss HMS HLS HSUV = μMV Ha: Hss *HMS *HLS*HSUV * HMV C. Ho Hss HMS HLS HSUV =μMV = = H: Not all the means are equal. D. Ho Hss HMS HLS HSUV HMV Ha Hss HMS HLS =HSUV = HMVarrow_forwardQuestion: A company launches two different marketing campaigns to promote the same product in two different regions. After one month, the company collects the sales data (in units sold) from both regions to compare the effectiveness of the campaigns. The company wants to determine whether there is a significant difference in the mean sales between the two regions. Perform a two sample T-test You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. (2 points = 0.5 x 4 Answers) Each of these is worth 0.5 points. However, showing the calculation is must. If calculation is missing, the whole answer won't get any credit.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL



