
Concept explainers
Archimedes’ Principle states that the buoyant force on an object partially or fully submerged in a fluid is equal to the weight of the fluid that the object displaces. Thus, for an object of density ρ0, floating partly submerged in a fluid of density ρf, the buoyant force is given by
(a) Show that the percentage of the volume of the object above the surface of the liquid is
(b) The density of ice is 917 kg/m3 and the density of seawater is 1030 kg/m3. What percentage of the volume of an iceberg is above water?
(c) An ice cube floats in a glass filled to the brim with water. Does the water overflow when the ice melts?
(d) A sphere of radius 0.4 m and having negligible weight is floating in a large freshwater lake. How much work is required to completely submerge the sphere? The density of the water is 1000 kg/m3.
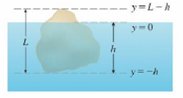
FIGURE FOR PROBLEM 6
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
CALCULUS, EARLY TRANSITIONS (LL)
- Good Day, Would appreciate any assistance with this query. Regards,arrow_forwardThis question builds on an earlier problem. The randomized numbers may have changed, but have your work for the previous problem available to help with this one. A 4-centimeter rod is attached at one end to a point A rotating counterclockwise on a wheel of radius 2 cm. The other end B is free to move back and forth along a horizontal bar that goes through the center of the wheel. At time t=0 the rod is situated as in the diagram at the left below. The wheel rotates counterclockwise at 1.5 rev/sec. At some point, the rod will be tangent to the circle as shown in the third picture. A B A B at some instant, the piston will be tangent to the circle (a) Express the x and y coordinates of point A as functions of t: x= 2 cos(3πt) and y= 2 sin(3t) (b) Write a formula for the slope of the tangent line to the circle at the point A at time t seconds: -cot(3πt) sin(3лt) (c) Express the x-coordinate of the right end of the rod at point B as a function of t: 2 cos(3πt) +411- 4 -2 sin (3лt) (d)…arrow_forward5. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.AE.003. y y= ex² 0 Video Example x EXAMPLE 3 (a) Use the Midpoint Rule with n = 10 to approximate the integral कर L'ex² dx. (b) Give an upper bound for the error involved in this approximation. SOLUTION 8+2 1 L'ex² d (a) Since a = 0, b = 1, and n = 10, the Midpoint Rule gives the following. (Round your answer to six decimal places.) dx Ax[f(0.05) + f(0.15) + ... + f(0.85) + f(0.95)] 0.1 [0.0025 +0.0225 + + e0.0625 + 0.1225 e0.3025 + e0.4225 + e0.2025 + + e0.5625 €0.7225 +0.9025] The figure illustrates this approximation. (b) Since f(x) = ex², we have f'(x) = 0 ≤ f'(x) = < 6e. ASK YOUR TEACHER and f'(x) = Also, since 0 ≤ x ≤ 1 we have x² ≤ and so Taking K = 6e, a = 0, b = 1, and n = 10 in the error estimate, we see that an upper bound for the error is as follows. (Round your final answer to five decimal places.) 6e(1)3 e 24( = ≈arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

