Essentials of Statistics (5th Edition)
5th Edition
ISBN: 9780321924599
Author: Mario F. Triola
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6, Problem 6FDD
Critical Thinking:
Designing aircraft seats
When designing seats for aircraft, we want to have sufficient room so that passengers are comfortable and safe, but we don’t want too much room, because fewer seats could be installed and profits would drop. It has been estimated that removing one row of seats would cost around $8 million over the life of an aircraft.
Figure 6-22(a) shows an important human consideration: The buttock-to-knee length. The accompanying table includes relevant buttock- to-knee length parameters obtained from studies of large numbers of people. Figure 6-22(b) shows a traditional aircraft seat, and Figure 6-22(c) shows the new SkyRider seat design by the Italian company Aviointeriors. The SkyRider seat is dramatically different from traditional aircraft seats. The seats are like saddles, and they are higher so that passenger legs slant downward with weight on the legs. The most dramatic difference is that SkyRider seats have much less legroom. The distance of 23 in. shown in Figure 6-22(c) is a distance of 30 in. to 32 in. for most current economy seats. As of this writing, the SkyRider seats have not yet been approved by the Federal Aviation Administration, but approval would allow a new class of seating with very low fares.
When designing aircraft seats, we must make some hard choices. If we are to accommodate everyone in the population, we will have a sitting distance that is so costly in terms of reduced seating that it might not be economically feasible. Some questions we must address are: (1) What percentage of the population are we willing to exclude? (2) How much extra room do we want to provide for passenger comfort and safety?
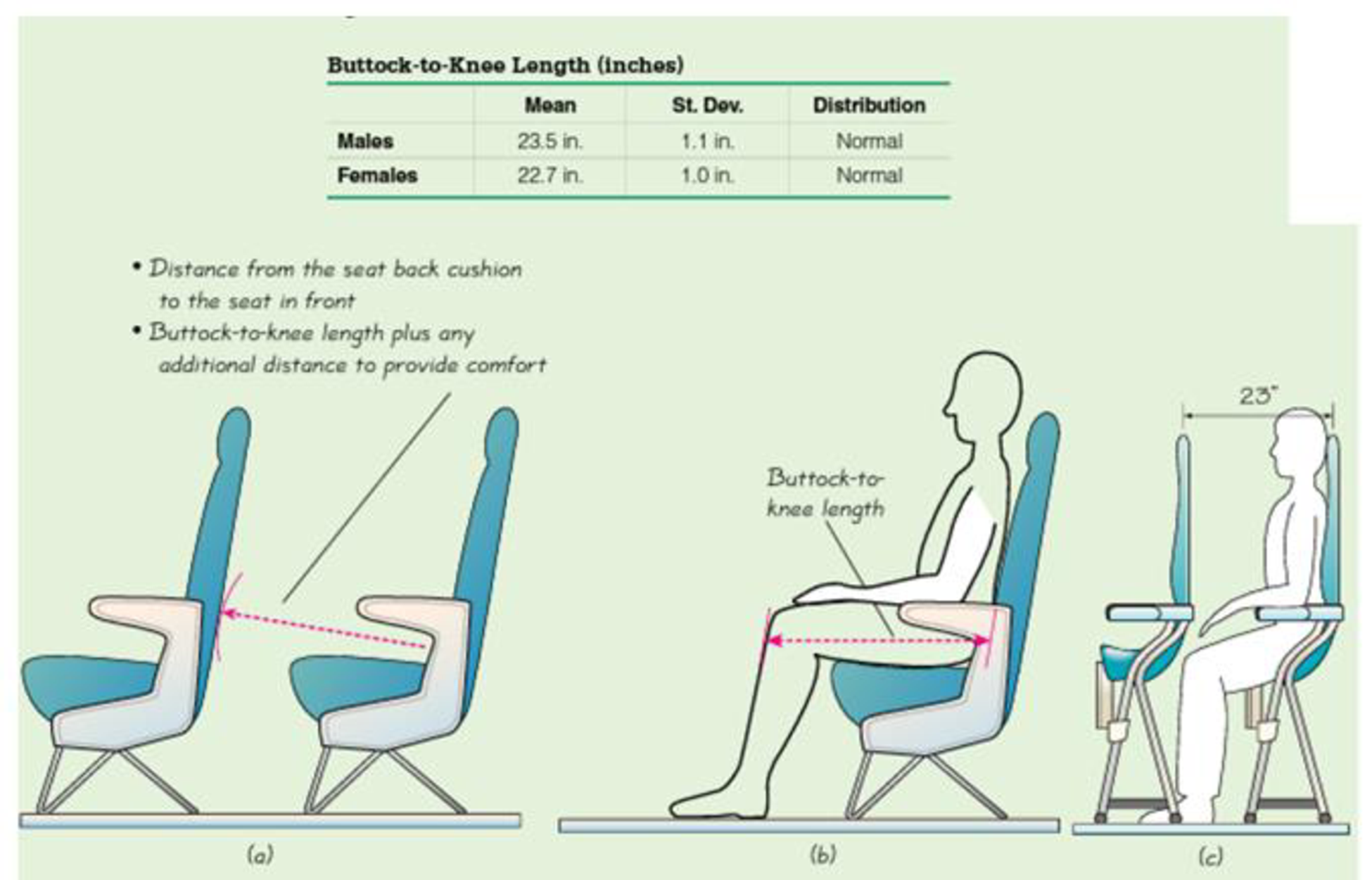
Figure 6-22 Distances Used In the Design of Aircraft Seats
6. Based on the preceding results, what would you tell an engineer who is designing and configuring seats for an aircraft?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(b) For a given sequence A, of subsets of 92, explain when we say that A,, has a
limit.
1. Let 2 (a, b, c} be the sample space.
(b) Construct a a-field containing A = {a, b} and B = {b, c}.
2=
1. Let 2 {a, b, c} be the sample space.
(a) Write down the power set of 2.
Chapter 6 Solutions
Essentials of Statistics (5th Edition)
Ch. 6.2 - Normal Distribution When we refer to a normal...Ch. 6.2 - Normal Distribution A normal distribution is...Ch. 6.2 - Standard Normal Distribution Identify the...Ch. 6.2 - Notation What does the notation Z indicate?Ch. 6.2 - Continuous Uniform Distribution. In Exercises 58,...Ch. 6.2 - Continuous Uniform Distribution. In Exercises 58,...Ch. 6.2 - Continuous Uniform Distribution. In Exercises 58,...Ch. 6.2 - Continuous Uniform Distribution. In Exercises 58,...Ch. 6.2 - Prob. 9BSCCh. 6.2 - Standard Normal Distribution. In Exercises 912,...
Ch. 6.2 - Prob. 11BSCCh. 6.2 - Prob. 12BSCCh. 6.2 - Prob. 13BSCCh. 6.2 - Prob. 14BSCCh. 6.2 - Prob. 15BSCCh. 6.2 - Prob. 16BSCCh. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Prob. 26BSCCh. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Prob. 28BSCCh. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 1736,...Ch. 6.2 - Standard Normal Distribution. In Exercises 17-36,...Ch. 6.2 - Standard Normal Distribution. In Exercises 17-36,...Ch. 6.2 - Prob. 35BSCCh. 6.2 - Prob. 36BSCCh. 6.2 - Finding Bone Density Scores. In Exercises 37-40...Ch. 6.2 - Finding Bone Density Scores. In Exercises 37-40...Ch. 6.2 - Prob. 39BSCCh. 6.2 - Finding Bone Density Scores. In Exercises 37-40...Ch. 6.2 - Finding Critical Values. In Exercises 41-44, find...Ch. 6.2 - Prob. 42BSCCh. 6.2 - Prob. 43BSCCh. 6.2 - Prob. 44BSCCh. 6.2 - Prob. 45BSCCh. 6.2 - Prob. 46BSCCh. 6.2 - Prob. 47BSCCh. 6.2 - Prob. 48BSCCh. 6.2 - Prob. 49BBCh. 6.2 - Distributions In a continuous uniform...Ch. 6.3 - Pulse Rates Pulse rates of women are normally...Ch. 6.3 - IQ Scores The Wechsler Adult Intelligence Scale is...Ch. 6.3 - Prob. 3BSCCh. 6.3 - Random Digits Computers are commonly used to...Ch. 6.3 - IQ Scores. In Exercises 5-8, find the area of the...Ch. 6.3 - Prob. 6BSCCh. 6.3 - Prob. 7BSCCh. 6.3 - Prob. 8BSCCh. 6.3 - Prob. 9BSCCh. 6.3 - Prob. 10BSCCh. 6.3 - Prob. 11BSCCh. 6.3 - Prob. 12BSCCh. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - IQ Scores. In Exercises 13-20, assume that adults...Ch. 6.3 - In Exercises 21-24, use these parameters (based on...Ch. 6.3 - In Exercises 21-24, use these parameters (based on...Ch. 6.3 - Prob. 23BSCCh. 6.3 - In Exercises 21-24, use these parameters (based on...Ch. 6.3 - Water Taxi Safety When a water taxi sank in...Ch. 6.3 - Prob. 26BSCCh. 6.3 - Prob. 27BSCCh. 6.3 - Prob. 28BSCCh. 6.3 - Prob. 29BSCCh. 6.3 - Aircraft Seat Width Engineers want to design seats...Ch. 6.3 - Chocolate Chip Cookies The Chapter Problem for...Ch. 6.3 - Quarters After 1964, quarters were manufactured so...Ch. 6.3 - Large Data Sets. In Exercises 33 and 34, refer to...Ch. 6.3 - Prob. 34BSCCh. 6.3 - Curving Test Scores A statistics professor gives a...Ch. 6.3 - Using Continuity Correction There are many...Ch. 6.3 - Prob. 37BBCh. 6.3 - SAT and ACT Tests Based on recent results, scores...Ch. 6.4 - Minting Quarters In a recent year, the U.S. Mint...Ch. 6.4 - Sampling with Replacement In a recent year, the...Ch. 6.4 - Unbiased Estimators Data Set 1 in Appendix B...Ch. 6.4 - Prob. 4BSCCh. 6.4 - Prob. 5BSCCh. 6.4 - Prob. 6BSCCh. 6.4 - Prob. 7BSCCh. 6.4 - In Exercises 710, use the same population of {4,...Ch. 6.4 - In Exercises 710, use the same population of {4,...Ch. 6.4 - Prob. 10BSCCh. 6.4 - In Exercises 1114, use the population of ages {56,...Ch. 6.4 - In Exercises 1114, use the population of ages {56,...Ch. 6.4 - In Exercises 1114, use the population of ages {56,...Ch. 6.4 - Prob. 14BSCCh. 6.4 - Births: Sampling Distribution of Sample Proportion...Ch. 6.4 - Births: Sampling Distribution of Sample Proportion...Ch. 6.4 - SAT and ACT Tests Because they enable efficient...Ch. 6.4 - Quality Control After constructing a new...Ch. 6.4 - Prob. 19BBCh. 6.4 - Prob. 20BBCh. 6.5 - Standard Error of the Mean The population of...Ch. 6.5 - Small Sample Heights of adult females are normally...Ch. 6.5 - Notation The population of distances that adult...Ch. 6.5 - Prob. 4BSCCh. 6.5 - Using the Central Limit Theorem. In Exercises 510,...Ch. 6.5 - Using the Central Limit Theorem. In Exercises 510,...Ch. 6.5 - Using the Central Limit Theorem. In Exercises 510,...Ch. 6.5 - Using the Central Limit Theorem. In Exercises 510,...Ch. 6.5 - Using the Central Limit Theorem. In Exercises 510,...Ch. 6.5 - Using the Central Limit Theorem. In Exercises 510,...Ch. 6.5 - Prob. 11BSCCh. 6.5 - Prob. 12BSCCh. 6.5 - Designing Hats Women have head circumferences that...Ch. 6.5 - Designing Manholes According to the website...Ch. 6.5 - Prob. 15BSCCh. 6.5 - Loading MM Packages MM plain candies have a mean...Ch. 6.5 - Prob. 17BSCCh. 6.5 - Pulse Rates of Women Women have pulse rates that...Ch. 6.5 - Redesign of Ejection Seats When women were allowed...Ch. 6.5 - Loading a Tour Boat The Ethan Allen tour boat...Ch. 6.5 - Doorway Height The Boeing 757-200 ER airliner...Ch. 6.5 - Loading Aircraft Before every flight, the pilot...Ch. 6.5 - Prob. 23BBCh. 6.5 - Population Parameters Use the same population of...Ch. 6.6 - Normal Quantile Plot Data Set 1 in Appendix B...Ch. 6.6 - Prob. 2BSCCh. 6.6 - Prob. 3BSCCh. 6.6 - Prob. 4BSCCh. 6.6 - Prob. 5BSCCh. 6.6 - Interpreting Normal Quantile Plots. In Exercises...Ch. 6.6 - Prob. 7BSCCh. 6.6 - Interpreting Normal Quantile Plots. In Exercises...Ch. 6.6 - Prob. 9BSCCh. 6.6 - Determining Normality. In Exercises 912, refer to...Ch. 6.6 - Determining Normality. In Exercises 912, refer to...Ch. 6.6 - Prob. 12BSCCh. 6.6 - Prob. 13BSCCh. 6.6 - Prob. 14BSCCh. 6.6 - Using Technology to Generate Normal Quantile...Ch. 6.6 - Prob. 16BSCCh. 6.6 - Prob. 17BSCCh. 6.6 - Constructing Normal Quantile Plots. In Exercises...Ch. 6.6 - Prob. 19BSCCh. 6.6 - Prob. 20BSCCh. 6.6 - Transformations The heights (in inches) of men...Ch. 6.6 - Earthquake Magnitudes Richter scale earthquake...Ch. 6.6 - Prob. 23BBCh. 6.7 - Exact Value and Approximation Refer to Figure 6-21...Ch. 6.7 - Continuity Correction In a preliminary test of the...Ch. 6.7 - Prob. 3BSCCh. 6.7 - Prob. 4BSCCh. 6.7 - Prob. 5BSCCh. 6.7 - Prob. 6BSCCh. 6.7 - Prob. 7BSCCh. 6.7 - Prob. 8BSCCh. 6.7 - Prob. 9BSCCh. 6.7 - Prob. 10BSCCh. 6.7 - Voters. In Exercises 912, use a normal...Ch. 6.7 - Prob. 12BSCCh. 6.7 - Prob. 13BSCCh. 6.7 - Prob. 14BSCCh. 6.7 - Mendelian Genetics When Mendel conducted his...Ch. 6.7 - Prob. 16BSCCh. 6.7 - XSORT Gender Selection MicroSorts XSORT...Ch. 6.7 - Prob. 18BSCCh. 6.7 - Prob. 19BSCCh. 6.7 - Cell Phones and Brain Cancer In a study of 420,095...Ch. 6.7 - Prob. 21BSCCh. 6.7 - Prob. 22BSCCh. 6.7 - Prob. 23BSCCh. 6.7 - Prob. 24BSCCh. 6.7 - Decision Theory Marc Taylor plans to place 200...Ch. 6.7 - Prob. 26BBCh. 6 - Identify the values of and for the standard...Ch. 6 - Bone Density Test. In Exercises 1-4, assume that...Ch. 6 - Prob. 3CQQCh. 6 - Prob. 4CQQCh. 6 - Prob. 5CQQCh. 6 - Prob. 6CQQCh. 6 - In Exercises 6-10, assume that red blood cell...Ch. 6 - Prob. 8CQQCh. 6 - Prob. 9CQQCh. 6 - Prob. 10CQQCh. 6 - Prob. 1RECh. 6 - Prob. 2RECh. 6 - Window Placement Standing eye heights of men are...Ch. 6 - Sampling Distributions Scores on the ACT test have...Ch. 6 - Prob. 5RECh. 6 - Monorail and Airliner Doors The Mark VI monorail...Ch. 6 - Aircraft Safety Standards Under older Federal...Ch. 6 - Assessing Normality Listed below are the current...Ch. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - Miami Heat The following are current annual...Ch. 6 - Prob. 2CRECh. 6 - Birth Weights Birth weights in the United States...Ch. 6 - POTUS The accompanying graph is a histogram of...Ch. 6 - Left-Handedness According to data from the...Ch. 6 - Binomial Probabilities Section 6-7 described a...Ch. 6 - Prob. 1FDDCh. 6 - Prob. 2FDDCh. 6 - Prob. 3FDDCh. 6 - Critical Thinking: Designing aircraft seats When...Ch. 6 - Critical Thinking: Designing aircraft seats When...Ch. 6 - Critical Thinking: Designing aircraft seats When...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- 1. Let 2 (a, b, c)} be the sample space. (a) Write down the power set of 2. (b) Construct a σ-field containing A = {a, b} and B = {b, c}. (c) Show that F= {0, 2, {a, b}, {b, c}, {b}} is not a σ-field. Add some elements to make it a σ-field..arrow_forward13. Let (, F, P) be a probability space and X a function from 2 to R. Explain when X is a random variable.arrow_forward24. A factory produces items from two machines: Machine A and Machine B. Machine A produces 60% of the total items, while Machine B produces 40%. The probability that an item produced by Machine A is defective is P(DIA)=0.03. The probability that an item produced by Machine B is defective is P(D|B)=0.05. (a) What is the probability that a randomly selected product be defective, P(D)? (b) If a randomly selected item from the production line is defective, calculate the probability that it was produced by Machine A, P(A|D).arrow_forward
- (b) In various places in this module, data on the silver content of coins minted in the reign of the twelfth-century Byzantine king Manuel I Comnenus have been considered. The full dataset is in the Minitab file coins.mwx. The dataset includes, among others, the values of the silver content of nine coins from the first coinage (variable Coin1) and seven from the fourth coinage (variable Coin4) which was produced a number of years later. (For the purposes of this question, you can ignore the variables Coin2 and Coin3.) In particular, in Activity 8 and Exercise 2 of Computer Book B, it was argued that the silver contents in both the first and the fourth coinages can be assumed to be normally distributed. The question of interest is whether there were differences in the silver content of coins minted early and late in Manuel’s reign. You are about to investigate this question using a two-sample t-interval. (i) Using Minitab, find either the sample standard deviations of the two variables…arrow_forwardHomework Let X1, X2, Xn be a random sample from f(x;0) where f(x; 0) = (-), 0 < x < ∞,0 € R Using Basu's theorem, show that Y = min{X} and Z =Σ(XY) are indep. -arrow_forwardHomework Let X1, X2, Xn be a random sample from f(x; 0) where f(x; 0) = e−(2-0), 0 < x < ∞,0 € R Using Basu's theorem, show that Y = min{X} and Z =Σ(XY) are indep.arrow_forward
- An Arts group holds a raffle. Each raffle ticket costs $2 and the raffle consists of 2500 tickets. The prize is a vacation worth $3,000. a. Determine your expected value if you buy one ticket. b. Determine your expected value if you buy five tickets. How much will the Arts group gain or lose if they sell all the tickets?arrow_forwardPlease show as much work as possible to clearly show the steps you used to find each solution. If you plan to use a calculator, please be sure to clearly indicate your strategy. Consider the following game. It costs $3 each time you roll a six-sided number cube. If you roll a 6 you win $15. If you roll any other number, you receive nothing. a) Find the expected value of the game. b) If you play this game many times, will you expect to gain or lose money?arrow_forward= 12:02 WeBWorK / 2024 Fall Rafeek MTH23 D02 / 9.2 Testing the Mean mu / 3 38 WEBWORK Previous Problem Problem List Next Problem 9.2 Testing the Mean mu: Problem 3 (1 point) Test the claim that the population of sophomore college students has a mean grade point average greater than 2.2. Sample statistics include n = 71, x = 2.44, and s = 0.9. Use a significance level of a = 0.01. The test statistic is The P-Value is between : The final conclusion is < P-value < A. There is sufficient evidence to support the claim that the mean grade point average is greater than 2.2. ○ B. There is not sufficient evidence to support the claim that the mean grade point average is greater than 2.2. Note: You can earn partial credit on this problem. Note: You are in the Reduced Scoring Period. All work counts for 50% of the original. Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining. . Oli wwm01.bcc.cuny.eduarrow_forward
- There are four white, fourteen blue and five green marbles in a bag. A marble is selected from the bag without looking. Find the odds of the following: The odds against selecting a green marble. The odds in favour of not selecting a green marble The odds in favor of the marble selected being either a white or a blue marble. What is true about the above odds? Explainarrow_forwardPlease show as much work as possible to clearly show the steps you used to find each solution. If you plan to use a calculator, please be sure to clearly indicate your strategy. 1. The probability of a soccer game in a particular league going into overtime is 0.125. Find the following: a. The odds in favour of a game going into overtime. b. The odds in favour of a game not going into overtime. c. If the teams in the league play 100 games in a season, about how many games would you expect to go into overtime?arrow_forwardexplain the importance of the Hypothesis test in a business setting, and give an example of a situation where it is helpful in business decision making.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY