
Throughout the picturesque valleys of mid-18th-century Germany echoed the song of the Neuländer (newlander), enticing journeymen who struggled to feed their families with the dream and promise of colonial America. The typical Neuländer sought to sign up several families from a village for immigration to a particular colony. By registering a group of neighbors, rather than isolated families, the agent increased the likelihood that his signees would not stray to the proposals of a competitor. Additionally, by signing large groups, the Neuländer fattened his purse, to the tune of one to two florins a head.
Generally, the Germans who chose to undertake the hardship of a trans-Atlantic voyage were poor, yet the cost of such a voyage was high. Records from a 1753 voyage indicate that the cost of an adult fare (one freight) from Rotterdam to Boston was 7.5 pistoles. Children aged 4 to 13 were assessed at half the adult rate (one-half freight) and those under 4 were not charged. To get a sense of the expense involved, an adult fare is equivalent to approximately $2000! Many immigrants did not have the necessary funds to purchase passage and, determined to make the crossing, paid with years of indentured servitude.
As a historian studying the influence of these German immigrants on colonial America, Hans Langenscheidt is interested in describing various demographic characteristics of these people. Unfortunately, accurate records are rare. He has discovered a partially reconstructed 1752 passenger list for a ship, the St. Andrew, containing the names of the heads of families, a list of family members traveling, their parish of origin, and the number of freights each family purchased. Unfortunately, some data are missing for some families. Langenscheidt believes that the demographic parameters of this passenger list are likely to be similar to those of the other voyages taken from Germany to America during the mid-18th century. Assuming that he is correct, he believes that it is appropriate to create a discrete
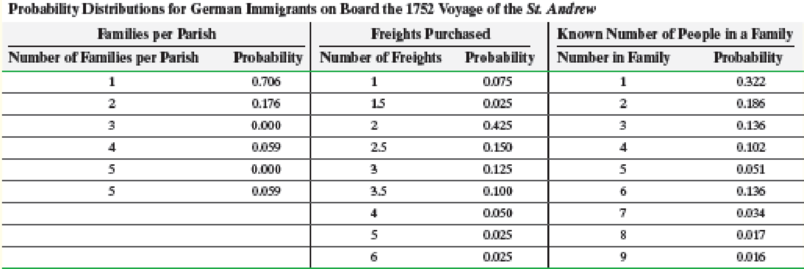
6. Summarize your findings in a report. Discuss any assumptions made throughout this analysis. What are the consequences to your calculations and conclusions if your assumptions are subsequently determined to be invalid?
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
MyLab Statistics with Pearson eText -- Standalone Access Card -- for Fundamentals of Statistics
- solve the question based on hw 1, 1.41arrow_forwardT1.4: Let ẞ(G) be the minimum size of a vertex cover, a(G) be the maximum size of an independent set and m(G) = |E(G)|. (i) Prove that if G is triangle free (no induced K3) then m(G) ≤ a(G)B(G). Hints - The neighborhood of a vertex in a triangle free graph must be independent; all edges have at least one end in a vertex cover. (ii) Show that all graphs of order n ≥ 3 and size m> [n2/4] contain a triangle. Hints - you may need to use either elementary calculus or the arithmetic-geometric mean inequality.arrow_forwardWe consider the one-period model studied in class as an example. Namely, we assumethat the current stock price is S0 = 10. At time T, the stock has either moved up toSt = 12 (with probability p = 0.6) or down towards St = 8 (with probability 1−p = 0.4).We consider a call option on this stock with maturity T and strike price K = 10. Theinterest rate on the money market is zero.As in class, we assume that you, as a customer, are willing to buy the call option on100 shares of stock for $120. The investor, who sold you the option, can adopt one of thefollowing strategies: Strategy 1: (seen in class) Buy 50 shares of stock and borrow $380. Strategy 2: Buy 55 shares of stock and borrow $430. Strategy 3: Buy 60 shares of stock and borrow $480. Strategy 4: Buy 40 shares of stock and borrow $280.(a) For each of strategies 2-4, describe the value of the investor’s portfolio at time 0,and at time T for each possible movement of the stock.(b) For each of strategies 2-4, does the investor have…arrow_forward
- Negate the following compound statement using De Morgans's laws.arrow_forwardNegate the following compound statement using De Morgans's laws.arrow_forwardQuestion 6: Negate the following compound statements, using De Morgan's laws. A) If Alberta was under water entirely then there should be no fossil of mammals.arrow_forward
- Negate the following compound statement using De Morgans's laws.arrow_forwardCharacterize (with proof) all connected graphs that contain no even cycles in terms oftheir blocks.arrow_forwardLet G be a connected graph that does not have P4 or C3 as an induced subgraph (i.e.,G is P4, C3 free). Prove that G is a complete bipartite grapharrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





